(→Linear Discriminant Functions) |
|||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [[Category:ECE662]] |
| + | [[Category:decision theory]] | ||
| + | [[Category:lecture notes]] | ||
| + | [[Category:pattern recognition]] | ||
| + | [[Category:slecture]] | ||
| − | |||
| + | <center><font size= 4> | ||
| + | '''[[ECE662]]: Statistical Pattern Recognition and Decision Making Processes''' | ||
| + | </font size> | ||
| + | |||
| + | Spring 2008, [[user:mboutin|Prof. Boutin]] | ||
| + | |||
| + | [[Slectures|Slecture]] | ||
| + | |||
| + | <font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | ||
| + | </center> | ||
| + | |||
| + | ---- | ||
| + | =Lecture 8 Lecture notes= | ||
| + | Jump to: [[ECE662_Pattern_Recognition_Decision_Making_Processes_Spring2008_sLecture_collective|Outline]]| | ||
| + | [[Lecture 1 - Introduction_OldKiwi|1]]| | ||
| + | [[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | ||
| + | [[Lecture 3 - Bayes classification_OldKiwi|3]]| | ||
| + | [[Lecture 4 - Bayes Classification_OldKiwi|4]]| | ||
| + | [[Lecture 5 - Discriminant Functions_OldKiwi|5]]| | ||
| + | [[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | ||
| + | [[Lecture 7 - MLE and BPE_OldKiwi|7]]| | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]]| | ||
| + | [[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]]| | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_OldKiwi|13]]| | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_OldKiwi|14]]| | ||
| + | [[Lecture 15 - Parzen Window Method_OldKiwi|15]]| | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_OldKiwi|16]]| | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_OldKiwi|17]]| | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_OldKiwi|18]]| | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_OldKiwi|19]]| | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_OldKiwi|20]]| | ||
| + | [[Lecture 21 - Decision Trees(Continued)_OldKiwi|21]]| | ||
| + | [[Lecture 22 - Decision Trees and Clustering_OldKiwi|22]]| | ||
| + | [[Lecture 23 - Spanning Trees_OldKiwi|23]]| | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_OldKiwi|24]]| | ||
| + | [[Lecture 25 - Clustering Algorithms_OldKiwi|25]]| | ||
| + | [[Lecture 26 - Statistical Clustering Methods_OldKiwi|26]]| | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_OldKiwi|27]]| | ||
| + | [[Lecture 28 - Final lecture_OldKiwi|28]] | ||
| + | ---- | ||
| + | ---- | ||
== Lecture Objective == | == Lecture Objective == | ||
* Maximum Likelihood Estimation and Bayesian Parameter Estimation | * Maximum Likelihood Estimation and Bayesian Parameter Estimation | ||
| Line 24: | Line 71: | ||
[[Image:BPEprocess_OldKiwi.jpg]] | [[Image:BPEprocess_OldKiwi.jpg]] | ||
| − | See also: [[Comparison of MLE and Bayesian Parameter Estimation_OldKiwi]] | + | See also: [[Comparison of MLE and Bayesian Parameter Estimation_OldKiwi|Comparison of MLE and Bayesian Parameter Estimation]] |
== Linear Discriminant Functions == | == Linear Discriminant Functions == | ||
| Line 83: | Line 130: | ||
'''For more information:''' | '''For more information:''' | ||
| − | [[Parametric Estimators_OldKiwi]] | + | [[Parametric Estimators_OldKiwi|Parametric Estimators]] |
| + | ---- | ||
| + | Previous: [[Lecture_7_-_MLE_and_BPE_OldKiwi|Lecture 7]] | ||
| + | Next: [[Lecture_9_-_Linear_Discriminant_Functions_OldKiwi|Lecture 9]] | ||
| − | + | [[ECE662:BoutinSpring08_OldKiwi|Back to ECE662 Spring 2008 Prof. Boutin]] | |
| − | [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 11:16, 10 June 2013
ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Contents
Lecture 8 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
Lecture Objective
- Maximum Likelihood Estimation and Bayesian Parameter Estimation
- Linear Discriminant Functions
Maximum Likelihood Estimation and Bayesian Parameter Estimation
If the prior distributions have some specific properties then the Bayesian Parameter Estimation and Maximum Likelihood Estimation are asymptotically equivalent for infinite training data. However, large training datasets are typically unavailable in pattern recognition problems. Furthermore, when the dimension of data increases, the complexity of estimating the parameters increases exponentially. In that aspect, BPE and MLE have some advantages over each other.
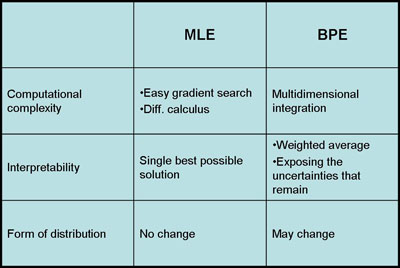
- Computational Complexity:
MLE has a better performance than BPE for large data, because MLE simply uses gradient or differential calculus to estimate the parameters. On the other hand, BPE uses high dimensional integration and it's computationally expensive.
- Interpretability:
The results of MLE are easier to interpret because it generates a single model to fit the data as much as possible. However, BPE generates a weighted sum of models which is harder to understand.
- Form of Distribution:
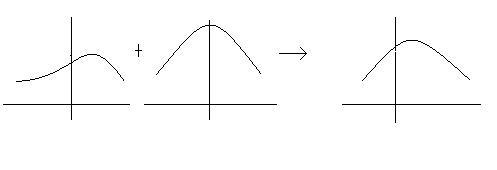
The advantage of using BPE is that it uses prior information that we have about the model and it gives us a possibility to sequentially update the model. If the information we have on the model is reliable than BPE is better than MLE. On the other hand, if prior model is uniformly distributed than BPE is not so different than MLE. Indeed, MLE is a special and simplistic form of BPE.
See also: Comparison of MLE and Bayesian Parameter Estimation
Linear Discriminant Functions
(From DHS Chapter 5)
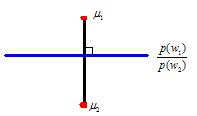
Suppose we have $ p(w_1|\vec{x}) $ and $ p(w_2|\vec{x}) $
$ g(\vec{x}) = p(w_1|\vec{x}) - p(w_2|\vec{x}) $
$ p(\vec{x}|w_i) $ -> Parametric Estimation Method
$ g(\vec{x}) $ -> proper form of Linear Discriminant Function
$ [1,x,x^2,x^3] $ -> new feature space
Simple and easy to design:
- 1 category case:
$ g(\vec{x}) = w\vec{x} + w_0 $
where $ w $ is the weight factor and $ w_0 $ is the bias of the threshold
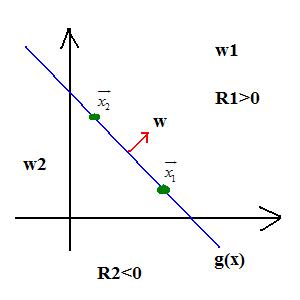
- 2 category case:
$ w_1, g(\vec{x}) > 0 $
$ w_2, g(\vec{x}) < 0 $
$ g(\vec{x}) = 0 $ : decision surface
$ g(\vec{x_1}) = w'\vec{x_1} + w_0 $
$ g(\vec{x_2}) = w'\vec{x_2} + w_0 $
$ w'\vec{x_1} + w_0 = w'\vec{x_2} + w_0 $
$ w'(\vec{x_1} - \vec{x_2}) = 0 $
- N category case:
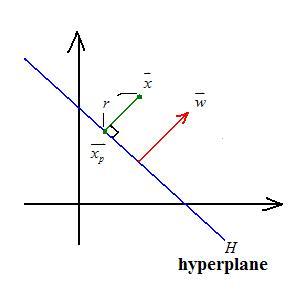
$ \vec{x} = \vec{x_p} + r\frac{\vec{w}}{|\vec{w}|} $
where $ \vec{x_p} $ is the projection point, $ r $ is the distance, and $ \frac{\vec{w}}{|\vec{w}|} $ is the unit normal
$ g(\vec{x}) = w'\vec{x} + w_0 = w'(\vec{x_p} + r\frac{\vec{w}}{|\vec{w}|}) + w_0 = w'\vec{x_p} + w_0 + w'r\frac{\vec{w}}{|\vec{w}|} = r|\vec{w}| $
therefore $ r = \frac{g(\vec{x})}{|\vec{w}|} $
For more information: