Lecture 20 Lecture notes

Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28

Density Estimation using Series Expansion

Last "non-parametric" technique (although very parametric)

Write $ p(\vec{x})=\sum _{j=0}^{\infty}c_j f_j (\vec{x}) \cong \sum _{j=0} ^{m}c_j f_j (\vec{x}) $ (1)

where {$ fj's $} are pre-determined class of functions

$ \vec{x} = (x_1, \cdots, x_n) $ (2)

Monomials: $ x_1 , x_1x_2 , x_1 ^3 $ (3)

Polynomials: $ x_1 + x_2 , x_1 + x_1 ^2 +x_1 x_2 $ (4)

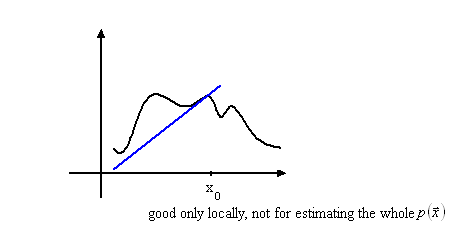
E.g.) Taylor expansion about $ x_0 $

In 1-D, $ p(x)=\sum _{j=1} ^ {\infty} \frac{p^{(j)} (x_0) (x-x_0)^j}{j!} $ (5) when $ p(x) $ is analytic

Taylor polynomial approximation

$ p(x) \approx \sum _{j=0} ^{m} \frac{p^{(j)}(x)(x-x_0)^j}{j!} $ (6) when $ p(x) \in C^{m+1}(\Re) $

$ p(x) \in C^{0}(\Re) $ means continuous
$ p(x) \in C^{1}(\Re) $ means differentiable once and continuous order derivative
$ p(x) \in C^{2}(\Re) $ means differentiable twice and continuous second order derivative

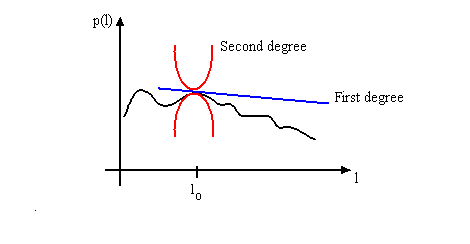
When m=1,linear approximation.

$ p(\vec{x})\approx c_0 + c \cdot (x-x_0) $ (7)

Figure 1

• Take hair length samples for men

Figure 2

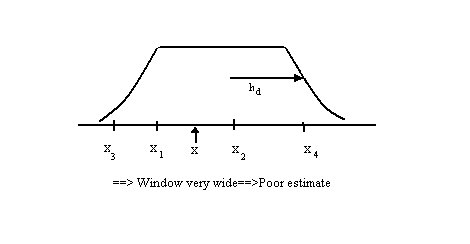
Must use "Parzen window" approach to approximate $ p(x) $

$ p(x) \cong \frac{K}{dV_d} $ (8), where K is number of samples in a neighborhood of x

              d is number of total samples

             $ V_d $ is volume of that neighborhood

There is relationship between series expansion and Parzen Windows.

Recall window function $ \Phi (\vec{x}) $

<<Picuture>>

$ \Phi (\frac{\vec{x}-\vec{x}_i}{h_d}) $ (9) used in approximating $ p(x) $

$ p(\vec{x}) \cong p_d(\vec{x})=\sum _{i=1} ^{d} \frac{1}{dV_d} \Phi (\frac{\vec{x}-\vec{x}_i}{h_d}) $ (10)

Want $ p_d (\vec{x})\cong \sum _{j=1} ^{m} c_j (x_i , \cdots, x_d)f_j (\vec{x}) $ (11)

Write $ \Phi (\vec{x})= \sum _{j=1} ^{m} c_j (x_i , \cdots, x_d)f_j (\vec{x}) $ (12)

By computing the series for $ \Phi (\vec {x}) \cong \sum _{j=1} ^{m} \vec {c}_j f_j (\vec{x}) $ (13)

Example) 1D Gaussian window and Tayor expansion

$ \Phi (u) = \frac{1}{\sqrt{\pi}} e ^{-u^2} $ (14)

We have $ \Phi (u)= \frac{1}{\sqrt{\pi}} \sum _{j=0} ^{\infty} \frac{{(-1)}^j u^{2j}}{j!} $ with |error|$ \leq \frac{1}{\sqrt{\pi}} \frac{u^{2m+1}}{(m+1)!} $ (15)

So for m=1,

$ \Phi (\frac{x-x_i}{h_d}) \cong \frac{1}{\sqrt{\pi}} - \frac{1}{\sqrt{\pi}} (\frac{x-x_i}{h_d})^2 = \frac{1}{\sqrt{\pi}} + \frac{2}{h_d ^2 \sqrt{\pi}} x x_i - \frac{1}{\sqrt{\pi} h_d ^2} x^2 - \frac{1}{\sqrt{\pi} h_d ^2} x_i ^2 $ (16)

<<Picture>>

$ \tilde{c} _0 (x_i) = \frac{1}{\sqrt{\pi}} - \frac{1}{\sqrt{\pi} h_d ^2}x_i ^2 $ (17)

$ \tilde{c} _1 = \frac{2}{\sqrt{\pi} h_d ^2}x_i $ (18)

$ \tilde{c} _2 = - \frac{1}{\sqrt{\pi} h_d ^2} $ (19)

So $ p_d (\vec{x}) \cong \sum _{j=0} ^{2} (\frac{1}{dV_d}\sum _{i=1} ^{d}\tilde{c}_j (x_i)) x^j $ (20)

, where $ c_0 = \frac{1}{dV_d} \sum _{i=1} ^{d} \tilde {c}_0 (x_i) = \frac{1}{d h_d} (\sum _{i=1} ^{d} \frac{1}{\sqrt{\pi}}- \frac{1}{\sqrt{\pi}h_d ^2}x_i ^2) $ (21)

$ c_1 = \frac{1}{d V_d} \sum _{i=1} ^{d} \frac{2}{h_d ^2 \sqrt{\pi}}x_i $ (22)

$ c_2 = - \frac{1}{h_d ^3} $ (23)

|error| less than $ \frac{1}{\sqrt{\pi}} \sum _{i=1} ^{d} \frac{{(x-x_i)}^4}{{h_d}^4 4!}= \frac{1}{\sqrt{\pi} 4!} \sum _{i=1} ^{d} \frac{{(x-x_i)}^4}{{h_d}^4} $

• This is samll when $ \ | \frac{(x-x_i)}{h_d}| $ is small for all i's

==> Need to be within distance $ \ h_d $ of all of your samples

Figure 3

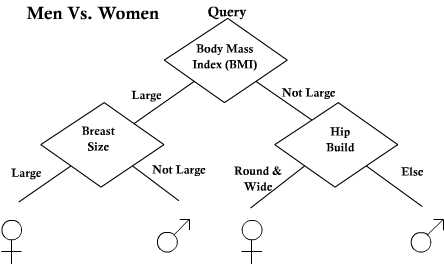
Decision Trees

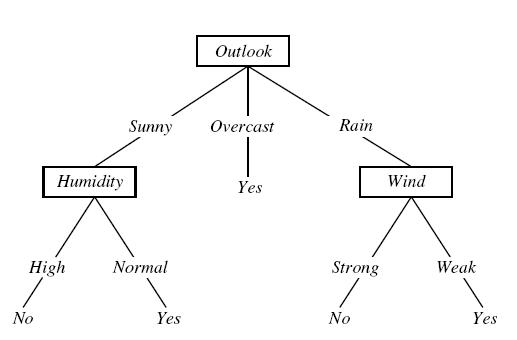
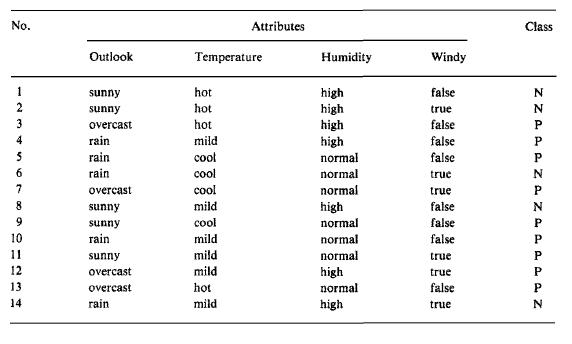
Reference DHS Chapter 8 Decision tree is one of the most powerful method for classification, because it simplifies the classification by dividing the problem into subproblems. A sample decision tree and training set from J.R. Quinlan (Induction of Decision Trees) can be given as follows:

The decision tree separates two classes. First class is "play tennis" and the second one is "do not play tennis". The decision tree tries to find the answer by asking several question. The purpose is to generate decision tree using the training data.

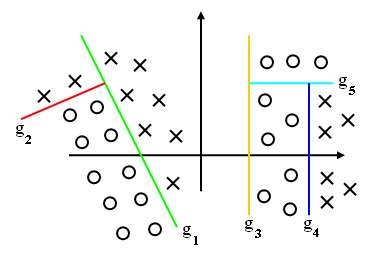
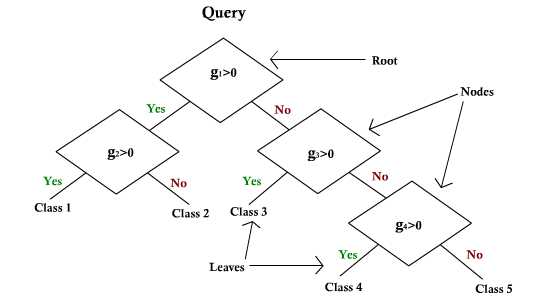
Instead of asking a complicated question $ g(x) >= 0 or <0 $

The idea: Ask a series of simple questions following a tree structure (linear 1-D).

Figure 4

Previous: Lecture 19 Next: Lecture 21

Back to ECE662 Spring 2008 Prof. Boutin