Lecture 22 Lecture notes

Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28

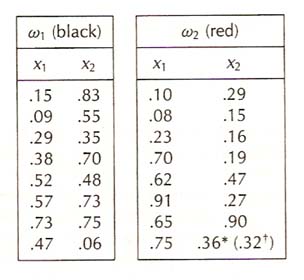
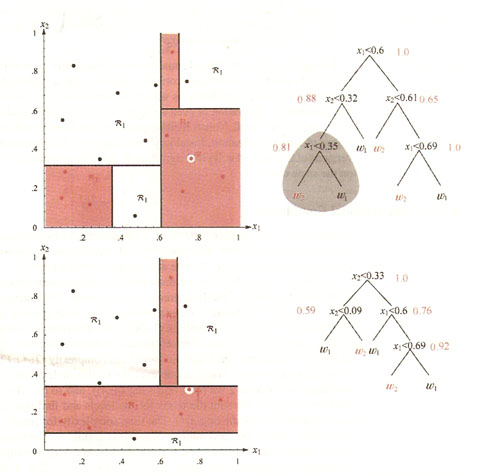
Note: Most tree growing methods favor greatest impurity reduction near the root node.

Example:

Figure 1

To assign category to a leaf node.

Easy! 
 
If sample data is pure
 
-> assign this class to leaf.
 
else
 
-> assign the most frequent class.

Note: Problem of building decision tree is "ill-conditioned"

i.e. small variance in the training data can yield large variations in decision rules obtained.

Ex. p.405(Duda & Hart)

A small move of one sample data can change the decision rules a lot.

Clustering References

"Data clustering, a review," A.K. Jain, M.N. Murty, P.J. Flynn[1]

"Algorithms for clustering data," A.K. Jain, R.C. Dibes[2]

"Support vector clustering," Ben-Hur, Horn, Siegelmann, Vapnik [3]

"Dynamic cluster formation using level set methods," Yip, Ding, Chan[4]

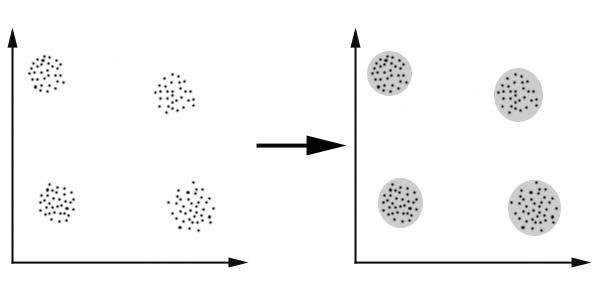
What is clustering?

The task of finding "natural " groupings in a data set. Clustering is one of the most important unsupervised learning technique. Basically, it tries to find the structure of unlabeled data, that is, based on some distance measure, it tries to group the similar members. Here is a simple figure from [5]:

Clustering algorithms can also be classified as follows:

• Exclusive Clustering
• Overlapping Clustering
• Hierarchical Clustering
• Probabilistic Clustering

There are several clustering techniques, the most important ones are:\

• K-means Clustering(exclusive)

• Fuzzy C-means(Overlapping)

• Hierarchical clustering

• Mixture of Gaussians(Probabilistic)

Here are some useful links for getting information & source about each clustering techniques.

• http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/index.html
• http://mvhs.shodor.org/mvhsproj/clustering/MatClust2.html
• http://www.lottolab.org/DavidCorney/ClusteringMatlab.html

Synonymons="unsupervised learning"

Figure 2

Figure 3

Clustering as a useful technique for searching in databases

Clustering can be used to construct an index for a large dataset to be searched quickly.

• Definition: An index is a data structure that enables sub-linear time look up.

• Example: Dewey system to index books in a library

Figure 4

• Example of Index: Face Recognition

- need face images with label

- must cluster to obtain sub-linear search time

- Search will be faster because of $ \bigtriangleup $ inequality.

Figure 5

• Example: Image segmentation is a clustering problem

- dataset = pixels in image

- each cluster is an object in image

Figure 6

Here is another example for image segmentation and compression from [6]

As can be seen, there is a trade-off between compression and image quality when the clustering is considered. The clustering is based on the similarity of colors. The most common color values are chosen to be k-means. Larger values of k increases the image quality while compression rate decrease.

Input to a clustering algorithm is either

• distances between each pairs of objects in dataset

• feature vectors for each object in dataset

Previous: Lecture 21 Next: Lecture 23

Back to ECE662 Spring 2008 Prof. Boutin