ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Contents
[hide]Lecture 4 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
Bayes decision rule for continuous features
Let $ \mathbf{x} = \left[ x_1, x_2, \cdots,x_n \right] ^{\mathbf{T}} $ be a random vector taking values in $ \Re^{n} $. X is characterized by its pdf (probability density function) and cdf (cumulative distribution function), or simply probability distribution function.
The cumulative distribution function or CDF is defined as: $ P({x}) = P(x_1,\cdots,x_n) = Pr\{x_1 \le X_1, \cdots, x_n \le X_n\} $
The probability density function or pdf is defined as: $ p({x}) = p(x_1,\cdots , x_n) = \displaystyle \lim_{\Delta x_i \rightarrow 0 , \forall i }{\frac{Pr\{x_1 \le X_1 \le x_1+ \Delta x_1, \cdots, x_n \le X_n \le x_n+ \Delta x_n\}}{\Delta x_1 \Delta x_2 \cdots \Delta x_n} } $
and Each class $ \omega_1, \cdots, \omega_k $ has its "conditional density"
$ p(x|w_i), i =1,\ldots,K $
Each $ p(x|w_i) $ is called "class i density" in contrast to the "unconditional density function of x", also called "mixture density of x" given by:
$ \displaystyle p({x}) = \sum_{k=1}^{K}P(w_i)p(x|w_i) $
Addendum to the lecture -- Since the classes $ \omega_i $ are discrete, P($ \omega_i $) is not the Probability Distribution Function or CDF of $ \omega_i $. Rather, it is the Probability Mass Function or pmf. Refer to duda and hart, page 21.
Bayes Theorem:
$ p(w_i|{x}) = \frac{\displaystyle p(x|w_i)P(w_i)}{\displaystyle {\sum_{k=1}^{K}p(x|w_k)P(w_k)}} $
Bayes Rule: Given X=x, decide $ \omega_i $ if
$ p(w_i|x) \ge p(w_j|x), \forall j $
$ \Longleftrightarrow p(x|w_i) \frac{\displaystyle P(w_i)}{\displaystyle \sum_{k=1}^{K}p(x|w_k)P(w_k)} \ge p(x|w_j) \frac{\displaystyle P(w_j)}{\displaystyle \sum_{k=1}^{K}p(x|w_k)P(w_k)} , \forall j $
The Bayes rules to minimize the expected loss([Loss Functions]) or "Risk":
- We consider a slightly more general setting of k+2 classes:
$ w_1, \cdots, w_k $, D, O, where D="doubt class" and O="outlier/other class"
Let $ L(w_l|w_k) $ be the loss incurred by deciding class $ w_l $ when the class is $ w_k $
Usually, $ L(w_k|w_k)=0, \forall k $
If every misclassification is equally bad we define:
$ L(w_l|w_k)= \{ { 0, \quad l=k, correct, \quad 1, \quad l \neq k, incorrect} \} $
We could also include the cost of doubting:
$ L(w_l|w_k)= \{ {0, \quad l=k; \quad 1, \quad l \neq k; \quad d, \quad w_l=D} \} $
Example: Two classes of fish in a lake: trout and catfish
$ L(trout|catfish) = \$2 $
$ L(catfish|trout) = \$3 $
$ \displaystyle L(trout|trout) = 0 $
$ \displaystyle L(catfish|catfish)= 0 $
and, the cost of doubting: $ L(D|catfish) = L(D|trout) = \$0.50 $
The expected loss for deciding a class $ w_i $ given X=x (the "Risk") is defined as:
$ R(w_i|x) := \displaystyle \sum_{k=1}^{K} L(w_i|w_k)P(w_k|x) $
Consider the classifier c(x), a rule that gives a class $ w_i ,i=1..k $ for every feature vector x. The risk of c(x) is given by
$ R(c(x)|x) =\displaystyle \sum_{k=1}^{K} L(c(x)|w_k)P(w_k|x) $
The overall risk:
$ R := \displaystyle \int R(c(x)|x)\rho(x)dx $
In order to minimize R we need to minimize R(c(x)|x) for every feature vector x.
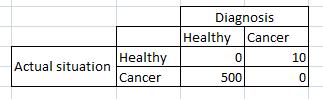
Example: Expected loss for making wrong decisions can also be represented by a loss matrix. Here is an instance for loss matrix:
If a patient is diagnosed as normal when s/he has cancer, the incurred loss will be much greater. However, the loss which is incurred when a patient is diagnosed as having cancer while s/he is not sick would be less. On the other hand, if the diagnosis is correct, no loss is incurred.
The optimum solution is to minimize expected loss which is the sum of the loss incurred by each misclassified class. This can be obtained by multiplication of the probability of being belong to wrong class and the loss incurred by that wrong decision.
Let's say, in a population, if the patient has cancer, the probability of making wrong decision is 5%, and if the patient is healthy, the probability of making wrong decision is 30%, then the expected loss based on the values given on the loss matrix can be calculated as follows:
Using the expected loss formula:
$ \displaystyle E[L] = 500*(5/100) + 0*(95/100) + 10*(30/100) + 0*(70/100) = 28 $
More generally, we will encounter similar issues when facing the task of rare event detection. In such cases, the impact of failing to detect one rare event would be a lot serious than the impact of false alarm (conclude detecting a rare event when actually it's not). Whenever the impact of mis-classificaiton is asymmetric or un-uniform, Risk would be a much more comprehensive performance metric than others like percentage accuracy.
Bayes rule to minimize the risk R:
Choose a class $ w_i $ that has the minimum risk $ R(w_i|x) $, i.e., choose $ w_i $ such that
$ R(w_i|x) \le R(w_j|x), \forall j $
$ \Longleftrightarrow \displaystyle \sum_{k=1}^{K} L(w_i|w_k)P(w_k|x) \le \displaystyle \sum_{k=1}^{K} L(w_j|w_k)P(w_k|x), \forall j $
$ \Longleftrightarrow \displaystyle \sum_{k=1}^{K}L(w_i|w_k)p(x|w_k)\frac{\displaystyle P(w_k)}{\displaystyle \sum_{l=1}^{K}p(x|w_l)P(w_l)} \le \displaystyle \sum_{k=1}^{K}L(w_j|w_k)p(x|w_k)\frac{\displaystyle P(w_k)}{\displaystyle \sum_{l=1}^{K}p(x|w_l)P(w_l)}, \forall j $
$ \Longleftrightarrow \displaystyle \sum_{k=1}^{K} L(w_i|w_k)p(x|w_k)P(w_k) \le \displaystyle \sum_{k=1}^{K} L(w_j|w_k)p(x|w_k)P(w_k), \text{for all j} $
Experiments and notes
- Bayes Classification: Experiments and Notes: Experiments with synthetic data. These experiments show the behavior of a Bayes Classification over classes with features with highly correlated data.