| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <center><font size= 4> | ||
| + | '''[[ECE662]]: Statistical Pattern Recognition and Decision Making Processes''' | ||
| + | </font size> | ||
| + | |||
| + | Spring 2008, [[user:mboutin|Prof. Boutin]] | ||
| + | |||
| + | [[Slectures|Slecture]] | ||
| + | |||
| + | <font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | ||
| + | </center> | ||
| + | |||
| + | ---- | ||
| + | =Lecture 17 Lecture notes= | ||
| + | Jump to: [[ECE662_Pattern_Recognition_Decision_Making_Processes_Spring2008_sLecture_collective|Outline]]| | ||
| + | [[Lecture 1 - Introduction_OldKiwi|1]]| | ||
| + | [[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | ||
| + | [[Lecture 3 - Bayes classification_OldKiwi|3]]| | ||
| + | [[Lecture 4 - Bayes Classification_OldKiwi|4]]| | ||
| + | [[Lecture 5 - Discriminant Functions_OldKiwi|5]]| | ||
| + | [[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | ||
| + | [[Lecture 7 - MLE and BPE_OldKiwi|7]]| | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]]| | ||
| + | [[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]]| | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_OldKiwi|13]]| | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_OldKiwi|14]]| | ||
| + | [[Lecture 15 - Parzen Window Method_OldKiwi|15]]| | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_OldKiwi|16]]| | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_OldKiwi|17]]| | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_OldKiwi|18]]| | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_OldKiwi|19]]| | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_OldKiwi|20]]| | ||
| + | [[Lecture 21 - Decision Trees(Continued)_OldKiwi|21]]| | ||
| + | [[Lecture 22 - Decision Trees and Clustering_OldKiwi|22]]| | ||
| + | [[Lecture 23 - Spanning Trees_OldKiwi|23]]| | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_OldKiwi|24]]| | ||
| + | [[Lecture 25 - Clustering Algorithms_OldKiwi|25]]| | ||
| + | [[Lecture 26 - Statistical Clustering Methods_OldKiwi|26]]| | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_OldKiwi|27]]| | ||
| + | [[Lecture 28 - Final lecture_OldKiwi|28]] | ||
| + | ---- | ||
| + | ---- | ||
'''Nearest Neighbor Classification Rule''' | '''Nearest Neighbor Classification Rule''' | ||
* useful when there are several labels | * useful when there are several labels | ||
| Line 37: | Line 81: | ||
Riemannian metric: <math>D(\vec{x_1},\vec{x_2})=\sqrt{(\vec{x_1}-\vec{x_2})^\top \mathbb{M}(\vec{x_1}-\vec{x_2})}</math> | Riemannian metric: <math>D(\vec{x_1},\vec{x_2})=\sqrt{(\vec{x_1}-\vec{x_2})^\top \mathbb{M}(\vec{x_1}-\vec{x_2})}</math> | ||
| − | Infinite norm: <math>D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{\ | + | Infinite norm: <math>D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{\infty}=max_i |{x_1}^i-{x_2}^i|</math> |
| Line 70: | Line 114: | ||
becasue shape defined by point is unchanged (invariant) by rotation and translation of triangles. | becasue shape defined by point is unchanged (invariant) by rotation and translation of triangles. | ||
| − | Therefore, distance between 2 triangles (or shapes) must be | + | Therefore, distance between 2 triangles (or shapes) must be independent on the position and orientation of triangles. |
'''Procrustes metric''' | '''Procrustes metric''' | ||
| Line 95: | Line 139: | ||
(p1,p2,p3) -> (new p1, new p2, new p3) | (p1,p2,p3) -> (new p1, new p2, new p3) | ||
| + | ---- | ||
| + | Previous: [[Lecture_16_-_Parzen_Window_Method_and_K-nearest_Neighbor_Density_Estimate_OldKiwi|Lecture 16]] | ||
| + | Next[[Lecture_18_-_Nearest_Neighbors_Clarification_Rule_and_Metrics(Continued)_OldKiwi|Lecture 18]] | ||
| − | [[Category: | + | [[ECE662:BoutinSpring08_OldKiwi|Back to ECE662 Spring 2008 Prof. Boutin]] |
| + | [[Category:ECE662]] | ||
| + | [[Category:decision theory]] | ||
| + | [[Category:lecture notes]] | ||
| + | [[Category:nearest neighbor]] | ||
| + | [[Category:pattern recognition]] | ||
| + | [[Category:slecture]] | ||
Latest revision as of 11:22, 10 June 2013
ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Lecture 17 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
Nearest Neighbor Classification Rule
- useful when there are several labels
- e.g. fingerprint-based recognition
Problem: Given the labeled training samples: $ \vec{X_1}, \vec{X_2}, \ldots, \vec{X_d} $ $ \in \mathbb{R}^n $ (or some other feature space) and an unlabeled test point $ \vec{X_0} $ $ \in \mathbb{R}^n $.
Classification: Let $ \vec{X_i} $ be the closest training point to $ \vec{X_0} $, then we assign the class of $ \vec{X_i} $ to $ \vec{X_0} $.
What do we mean by closest?
There are many meaning depending on the metric we choose for the feature space.
Definition A "metric" on a space S is a function
$ D: S\times S\rightarrow \mathbb{R} $
that satisfies the following 4 properties:
- Non-negativity $ D(\vec{x_1},\vec{x_2})\geq 0, \forall \vec{x_1},\vec{x_2}\in S $
- Symmetry $ D(\vec{x_1},\vec{x_2})=D(\vec{x_2},\vec{x_1}), \forall \vec{x_1},\vec{x_2}\in S $
- Reflexivity $ D(\vec{x},\vec{x})=0, \forall \vec{x}\in S $
- Triangle Inequality $ D(\vec{x_1},\vec{x_2})+D(\vec{x_2},\vec{x_3})\geq D(\vec{x_1},\vec{x_3}) , \forall \vec{x_1}, \vec{x_2}, \vec{x_3}\in S $
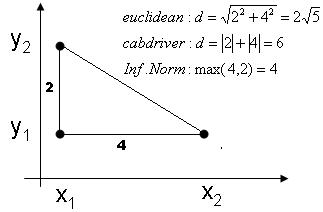 Illustration of 3 different metrics
Illustration of 3 different metrics
Examples of metrics
Euclidean distance: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_2}=\sqrt{\sum_{i=1}^n ({x_1}^i-{x_2}^i)^2} $
Manhattan (cab driver) distance: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_1}=\sum_{i=1}^n |{x_1}^i-{x_2}^i| $
Minkowski metric: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{L_p}=(\sum_{i=1}^n ({x_1}^i-{x_2}^i)^p)^{\frac{1}{p}} $
Riemannian metric: $ D(\vec{x_1},\vec{x_2})=\sqrt{(\vec{x_1}-\vec{x_2})^\top \mathbb{M}(\vec{x_1}-\vec{x_2})} $
Infinite norm: $ D(\vec{x_1},\vec{x_2})=||\vec{x_1}-\vec{x_2}||_{\infty}=max_i |{x_1}^i-{x_2}^i| $
where M is a symmetric positive definite $ n\times n $ matrix. Different choices for M enable associating different weights with different components.
In this way, we see that $ \mathbb{R}^n $, $ \mathbb{Z}^n $, $ \mathbb{C}^n $ have many natural metrics, but feature could be in some other set, e.g. a discrete set.
for example,
$ x_1 $={fever, skinrash, high blodd pressure}
$ x_2 $={fever, neckstiffness}
Tanimoto metric
$ D(set1, set2) = \frac {|set1|+|set2|-2|set1 \bigcap set2| }{|set1|+|set2|-|set1 \bigcap set2|} $
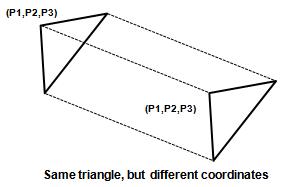
Example: previous approach to shape recognition Given is a set of ordered points in $ R_n =(p_1,p_2,\cdots,p_N) $ We want to recognize the shape
Given template (triangle form): (T1,T2,...,TN); We want to assign one of test template to a test (P1,P2,P3) In this case, we should not use Euclidean distance!,
becasue shape defined by point is unchanged (invariant) by rotation and translation of triangles.
Therefore, distance between 2 triangles (or shapes) must be independent on the position and orientation of triangles.
Procrustes metric
$ D(p,\bar p)= \sum_{\begin{matrix}i=1 \\ rotation R, translation T \end{matrix}}^n {\begin{Vmatrix} Rp_i+T-\bar p_i \end{Vmatrix}} _{L^2} $
$ p=(p_1, p_2, \cdots ,p_N),\bar p = (\bar p_1, \bar p_2, \cdots ,\bar p_N) $
Alternative approach "Use invariant coordinate to repeat $ p=(p_1, p_2, \cdots ,p_N) $ "
i.e find $ \varphi $ such that
$ \varphi : \mathbb{R}^n\rightarrow \mathbb{R}^k $ (where, typically $ k \leq n $)
s.t $ \varphi (x) = \varphi (\bar x) $
whenever $ \exists $ R, T with $ R \bar X + \bar T = X $
Example of phi with triangle (Figure 3):
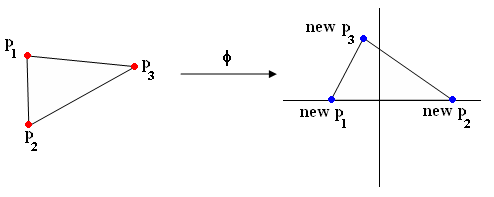
(p1,p2,p3) -> (new p1, new p2, new p3)
Previous: Lecture 16 NextLecture 18