| (3 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
Spring 2008, [[user:mboutin|Prof. Boutin]] | Spring 2008, [[user:mboutin|Prof. Boutin]] | ||
| − | + | [[Slectures|Slecture]] | |
<font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | <font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | ||
| Line 12: | Line 12: | ||
---- | ---- | ||
=Lecture 20 Lecture notes= | =Lecture 20 Lecture notes= | ||
| − | + | Jump to: [[ECE662_Pattern_Recognition_Decision_Making_Processes_Spring2008_sLecture_collective|Outline]]| | |
| + | [[Lecture 1 - Introduction_OldKiwi|1]]| | ||
[[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | [[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | ||
[[Lecture 3 - Bayes classification_OldKiwi|3]]| | [[Lecture 3 - Bayes classification_OldKiwi|3]]| | ||
| Line 19: | Line 20: | ||
[[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | [[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | ||
[[Lecture 7 - MLE and BPE_OldKiwi|7]]| | [[Lecture 7 - MLE and BPE_OldKiwi|7]]| | ||
| − | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]] | + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]]| |
[[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | [[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | ||
| − | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]] | + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]]| |
[[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | ||
[[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | ||
| Line 175: | Line 176: | ||
[[Category:lecture notes]] | [[Category:lecture notes]] | ||
[[Category:pattern recognition]] | [[Category:pattern recognition]] | ||
| − | [[Category: | + | [[Category:slecture]] |
Latest revision as of 11:23, 10 June 2013
ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Lecture 20 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
Density Estimation using Series Expansion
Last "non-parametric" technique (although very parametric)
Write $ p(\vec{x})=\sum _{j=0}^{\infty}c_j f_j (\vec{x}) \cong \sum _{j=0} ^{m}c_j f_j (\vec{x}) $ (1)
where {$ fj's $} are pre-determined class of functions
$ \vec{x} = (x_1, \cdots, x_n) $ (2)
Monomials: $ x_1 , x_1x_2 , x_1 ^3 $ (3)
Polynomials: $ x_1 + x_2 , x_1 + x_1 ^2 +x_1 x_2 $ (4)
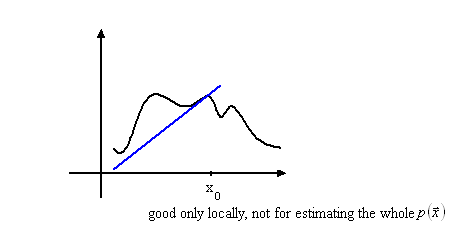
E.g.) Taylor expansion about $ x_0 $
In 1-D, $ p(x)=\sum _{j=1} ^ {\infty} \frac{p^{(j)} (x_0) (x-x_0)^j}{j!} $ (5) when $ p(x) $ is analytic
Taylor polynomial approximation
$ p(x) \approx \sum _{j=0} ^{m} \frac{p^{(j)}(x)(x-x_0)^j}{j!} $ (6) when $ p(x) \in C^{m+1}(\Re) $
$ p(x) \in C^{0}(\Re) $ means continuous $ p(x) \in C^{1}(\Re) $ means differentiable once and continuous order derivative $ p(x) \in C^{2}(\Re) $ means differentiable twice and continuous second order derivative
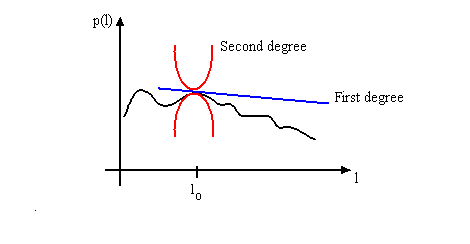
When m=1,linear approximation.
$ p(\vec{x})\approx c_0 + c \cdot (x-x_0) $ (7)
- Take hair length samples for men
Must use "Parzen window" approach to approximate $ p(x) $
$ p(x) \cong \frac{K}{dV_d} $ (8), where K is number of samples in a neighborhood of x
d is number of total samples
$ V_d $ is volume of that neighborhood
There is relationship between series expansion and Parzen Windows.
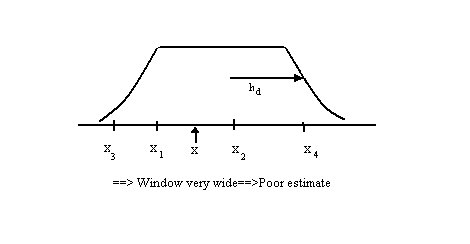
Recall window function $ \Phi (\vec{x}) $
<<Picuture>>
$ \Phi (\frac{\vec{x}-\vec{x}_i}{h_d}) $ (9) used in approximating $ p(x) $
$ p(\vec{x}) \cong p_d(\vec{x})=\sum _{i=1} ^{d} \frac{1}{dV_d} \Phi (\frac{\vec{x}-\vec{x}_i}{h_d}) $ (10)
Want $ p_d (\vec{x})\cong \sum _{j=1} ^{m} c_j (x_i , \cdots, x_d)f_j (\vec{x}) $ (11)
Write $ \Phi (\vec{x})= \sum _{j=1} ^{m} c_j (x_i , \cdots, x_d)f_j (\vec{x}) $ (12)
By computing the series for $ \Phi (\vec {x}) \cong \sum _{j=1} ^{m} \vec {c}_j f_j (\vec{x}) $ (13)
Example) 1D Gaussian window and Tayor expansion
$ \Phi (u) = \frac{1}{\sqrt{\pi}} e ^{-u^2} $ (14)
We have $ \Phi (u)= \frac{1}{\sqrt{\pi}} \sum _{j=0} ^{\infty} \frac{{(-1)}^j u^{2j}}{j!} $ with |error|$ \leq \frac{1}{\sqrt{\pi}} \frac{u^{2m+1}}{(m+1)!} $ (15)
So for m=1,
$ \Phi (\frac{x-x_i}{h_d}) \cong \frac{1}{\sqrt{\pi}} - \frac{1}{\sqrt{\pi}} (\frac{x-x_i}{h_d})^2 = \frac{1}{\sqrt{\pi}} + \frac{2}{h_d ^2 \sqrt{\pi}} x x_i - \frac{1}{\sqrt{\pi} h_d ^2} x^2 - \frac{1}{\sqrt{\pi} h_d ^2} x_i ^2 $ (16)
<<Picture>>
$ \tilde{c} _0 (x_i) = \frac{1}{\sqrt{\pi}} - \frac{1}{\sqrt{\pi} h_d ^2}x_i ^2 $ (17)
$ \tilde{c} _1 = \frac{2}{\sqrt{\pi} h_d ^2}x_i $ (18)
$ \tilde{c} _2 = - \frac{1}{\sqrt{\pi} h_d ^2} $ (19)
So $ p_d (\vec{x}) \cong \sum _{j=0} ^{2} (\frac{1}{dV_d}\sum _{i=1} ^{d}\tilde{c}_j (x_i)) x^j $ (20)
, where $ c_0 = \frac{1}{dV_d} \sum _{i=1} ^{d} \tilde {c}_0 (x_i) = \frac{1}{d h_d} (\sum _{i=1} ^{d} \frac{1}{\sqrt{\pi}}- \frac{1}{\sqrt{\pi}h_d ^2}x_i ^2) $ (21)
$ c_1 = \frac{1}{d V_d} \sum _{i=1} ^{d} \frac{2}{h_d ^2 \sqrt{\pi}}x_i $ (22)
$ c_2 = - \frac{1}{h_d ^3} $ (23)
|error| less than $ \frac{1}{\sqrt{\pi}} \sum _{i=1} ^{d} \frac{{(x-x_i)}^4}{{h_d}^4 4!}= \frac{1}{\sqrt{\pi} 4!} \sum _{i=1} ^{d} \frac{{(x-x_i)}^4}{{h_d}^4} $
- This is samll when $ \ | \frac{(x-x_i)}{h_d}| $ is small for all i's
==> Need to be within distance $ \ h_d $ of all of your samples
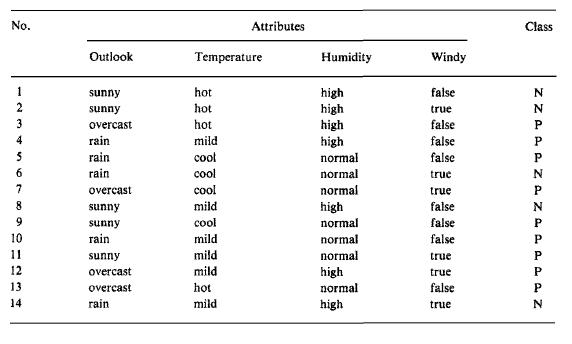
Decision Trees
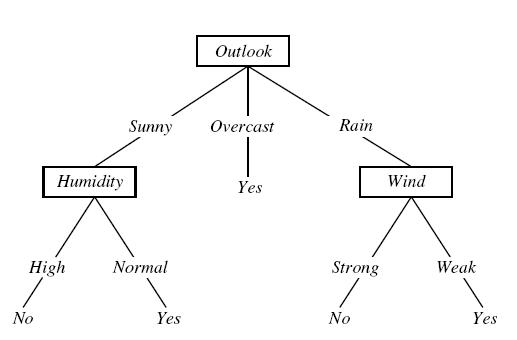
Reference DHS Chapter 8 Decision tree is one of the most powerful method for classification, because it simplifies the classification by dividing the problem into subproblems. A sample decision tree and training set from J.R. Quinlan (Induction of Decision Trees) can be given as follows:
The decision tree separates two classes. First class is "play tennis" and the second one is "do not play tennis". The decision tree tries to find the answer by asking several question. The purpose is to generate decision tree using the training data.
Instead of asking a complicated question $ g(x) >= 0 or <0 $
The idea: Ask a series of simple questions following a tree structure (linear 1-D).
Previous: Lecture 19 Next: Lecture 21