(New page: Category:math Category:tutorial Category:math squad Math Squad :↳ To Infinity and Beyond. Introduction ::↳ [[Math_Squa...) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
::↳ [[Math_Squad_infinity_review_of_set_theory__mhossain_S13|Review of Set Theory]] | ::↳ [[Math_Squad_infinity_review_of_set_theory__mhossain_S13|Review of Set Theory]] | ||
:::↳ [[Math_Squad_infinity_review_of_set_theory_function_mhossain_S13|Functions]] | :::↳ [[Math_Squad_infinity_review_of_set_theory_function_mhossain_S13|Functions]] | ||
| − | :::↳ Countability | + | :::↳ [[Math_Squad_infinity_review_of_set_theory_countablity_mhossain_S13|Countability]] |
| − | :::↳ Cardinality | + | :::↳ [[Math_Squad_infinity_review_of_set_theory_cardinality_mhossain_S13|Cardinality]] |
| − | ::↳ Hilbert's Grand Hotel | + | ::↳ [[Math_Squad_infinity_Hilbert_hotel_mhossain_S13|Hilbert's Grand Hotel]] |
| Line 27: | Line 27: | ||
---- | ---- | ||
| + | |||
Let <math>f</math> be a function from set <math>A</math> to set <math>B</math>. | Let <math>f</math> be a function from set <math>A</math> to set <math>B</math>. | ||
| Line 34: | Line 35: | ||
=== Onto (Surjective) === | === Onto (Surjective) === | ||
| − | Definition | + | '''Definition''' The function <math>f</math> is said to be '''surjective''' (or to map <math>A</math> '''onto''' <math>B</math>) if <math>f(A) = B</math>; that is, if the range <math>F(f) = B</math>. If <math>f</math> is a surjective function, we also say that <math>f</math> is a surjection. |
| − | In other words, if for every <math>y</math> in <math>B</math>, there exists at least one <math>x</math> in <math>A</math> such that <math>f(x) = y</math>, then <math>f</math> | + | In other words, if for every <math>y</math> in <math>B</math>, there exists at least one <math>x</math> in <math>A</math> such that <math>f(x) = y</math>, then <math>f</math> is '''onto''' <math>B</math>. |
e.g. Given that | e.g. Given that | ||
| Line 59: | Line 60: | ||
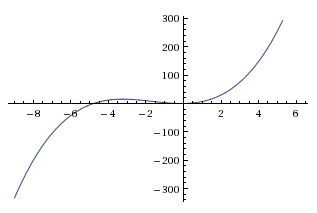
Figures one and two show some other examples of functions, one of which is onto and one which is not. | Figures one and two show some other examples of functions, one of which is onto and one which is not. | ||
| − | [[Image:functions_fig1_mh.jpeg|400px|thumb|left|<math>y = f(x) = x+5x^2+x^3, f:\mathbb{R}\rightarrow\mathbb{R}</math> | + | [[Image:functions_fig1_mh.jpeg|400px|thumb|left|<math>y = f(x) = x+5x^2+x^3, f:\mathbb{R}\rightarrow\mathbb{R}</math> <br/> |
Fig 1: <math>f</math> is onto since every value on the <math>y</math>-axis has at least one corresponding value on the <math>x</math>-axis]] | Fig 1: <math>f</math> is onto since every value on the <math>y</math>-axis has at least one corresponding value on the <math>x</math>-axis]] | ||
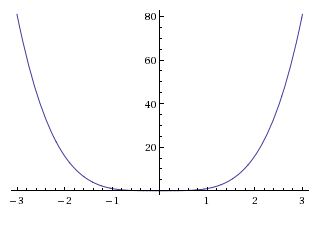
| − | [[Image:functions_fig2_mh.jpeg|400px|thumb|left|<math>y = f(x) = x^4, f:\mathbb{R}\rightarrow\mathbb{R}</math> | + | |
| − | Fig | + | |
| + | [[Image:functions_fig2_mh.jpeg|400px|thumb|left|<math>y = f(x) = x^4, f:\mathbb{R}\rightarrow\mathbb{R}</math> <br/> | ||
| + | Fig 2: <math>f</math> is not onto since there is no value on the <math>x</math>-axis that can produce a negative real number on the <math>y</math>-axis]] | ||
| + | |||
| + | |||
=== One-to-One (Injective) === | === One-to-One (Injective) === | ||
| − | Definition | + | '''Definition''' The function <math>f</math> is said to be '''injective''' (or to be '''one-one''') if whenever <math>x_1</math> is not equal to <math>x_2</math>, then <math>f(x_1)</math> is not equal to <math>f(x_2)</math>. If <math>f</math> is an injective function, we also say that <math>f</math> is a injection. |
In other words, if <math>x_1</math> and <math>x_2</math> are in the domain of <math>f</math> and if <math>f</math> is one-to-one if either of the following is true | In other words, if <math>x_1</math> and <math>x_2</math> are in the domain of <math>f</math> and if <math>f</math> is one-to-one if either of the following is true | ||
| Line 76: | Line 81: | ||
\end{align}</math> | \end{align}</math> | ||
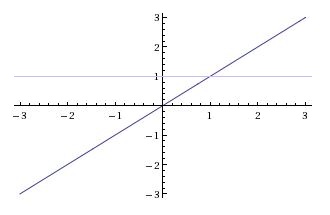
| − | + | You may recall the informal method of checking whether functions are one-to-one using the horizontal line test. This is illustrated in the following examples in figures three and four. | |
| − | + | ||
| − | + | ||
| − | + | [[Image:functions_fig3_mh.jpeg|400px|thumb|left|<math>y = f(x) = x, f:\mathbb{R}\rightarrow\mathbb{R}</math> <br/> | |
| + | Fig 3: Any arbitrary horizontal line <math>y = c</math> intersects the function's graph only once so we can infer that <math>f</math> is injective.]] | ||
| − | |||
| − | |||
| − | |||
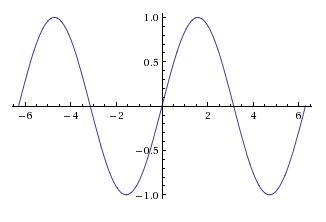
| − | + | [[Image:functions_fig4_mh.jpeg|400px|thumb|left|<math>y = f(x) = \sin(x), f:\mathbb{R}\rightarrow\mathbb{R}</math> <br/> | |
| + | Fig 3: The <math>x</math>-axis intersects the graph of the function multiple times. It does not pass the horizontal line test. Therefore we can conclude that <math>f</math> is not injective.]] | ||
| − | |||
| − | + | == Bijection == | |
| − | + | '''Definition''' If <math>f</math> is both injective and surjective, then <math>f</math> is said to be '''bijective'''. If <math>f</math> is bijective, we also say that <math>f</math> is a '''bijection''' | |
| − | |||
| − | + | The next section of this tutorial will cover the [[Math_Squad_infinity_review_of_set_theory_countablity_mhossain_S13|countability]] of sets. | |
| − | + | ||
| − | + | ||
| − | + | ---- | |
| − | + | ||
| − | + | ||
| − | == | + | == References == |
| − | + | ||
| − | + | * R. G. Bartle, D. R. Sherbert, "Preliminaries" in "An Introduction to Real Analysis", Third Edition, John Wiley and Sons Inc. 2000 ch. 1, sect. 1.1, pp 8. | |
| + | |||
| + | * R. Kenney. MA 301. "An Introduction to Proof through Real Analysis", Lecture Notes. Faculty of the Department of Mathematics, Purdue University, Spring 2012 | ||
| − | |||
---- | ---- | ||
| − | = | + | =Questions and comments= |
| − | + | If you have any questions, comments, etc. please post them below: | |
| + | |||
| + | *Comment / question 1 | ||
| + | |||
| + | |||
| + | ---- | ||
| − | + | [[Math_squad|Back to Math Squad page]] | |
Latest revision as of 16:51, 11 December 2013
- ↳ To Infinity and Beyond. Introduction
- ↳ Review of Set Theory
- ↳ Functions
- ↳ Countability
- ↳ Cardinality
- ↳ Hilbert's Grand Hotel
- ↳ Review of Set Theory
To Infinity and Beyond
A Review of Set Theory: Functions
by Maliha Hossain, proud member of the Math Squad
Let $ f $ be a function from set $ A $ to set $ B $.
$ \Leftrightarrow f : A \rightarrow B $
Contents
Onto (Surjective)
Definition The function $ f $ is said to be surjective (or to map $ A $ onto $ B $) if $ f(A) = B $; that is, if the range $ F(f) = B $. If $ f $ is a surjective function, we also say that $ f $ is a surjection.
In other words, if for every $ y $ in $ B $, there exists at least one $ x $ in $ A $ such that $ f(x) = y $, then $ f $ is onto $ B $.
e.g. Given that
$ f(x) = x^5, \forall x \in \mathbb{R}, f : \mathbb{R} \rightarrow \mathbb{R} $
then, $ f $ is onto the set R.
e.g. Given that
$ f(x) = x^2, \forall x \in \mathbb{R}, f : \mathbb{R} \rightarrow \mathbb{R} $
then, $ f $ is not onto the set R.
But if we define the domain of $ f $ such that
$ f(x) = x^2, \forall x \in \mathbb{R}, f : \mathbb{R} \rightarrow [0,\infty] $
then, $ f $ is not onto.
Figures one and two show some other examples of functions, one of which is onto and one which is not.
Fig 1: $ f $ is onto since every value on the $ y $-axis has at least one corresponding value on the $ x $-axis
Fig 2: $ f $ is not onto since there is no value on the $ x $-axis that can produce a negative real number on the $ y $-axis
One-to-One (Injective)
Definition The function $ f $ is said to be injective (or to be one-one) if whenever $ x_1 $ is not equal to $ x_2 $, then $ f(x_1) $ is not equal to $ f(x_2) $. If $ f $ is an injective function, we also say that $ f $ is a injection.
In other words, if $ x_1 $ and $ x_2 $ are in the domain of $ f $ and if $ f $ is one-to-one if either of the following is true
$ \begin{align} &\bullet x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2) \\ &\bullet f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \end{align} $
You may recall the informal method of checking whether functions are one-to-one using the horizontal line test. This is illustrated in the following examples in figures three and four.
Fig 3: Any arbitrary horizontal line $ y = c $ intersects the function's graph only once so we can infer that $ f $ is injective.
Fig 3: The $ x $-axis intersects the graph of the function multiple times. It does not pass the horizontal line test. Therefore we can conclude that $ f $ is not injective.
Bijection
Definition If $ f $ is both injective and surjective, then $ f $ is said to be bijective. If $ f $ is bijective, we also say that $ f $ is a bijection
The next section of this tutorial will cover the countability of sets.
References
- R. G. Bartle, D. R. Sherbert, "Preliminaries" in "An Introduction to Real Analysis", Third Edition, John Wiley and Sons Inc. 2000 ch. 1, sect. 1.1, pp 8.
- R. Kenney. MA 301. "An Introduction to Proof through Real Analysis", Lecture Notes. Faculty of the Department of Mathematics, Purdue University, Spring 2012
Questions and comments
If you have any questions, comments, etc. please post them below:
- Comment / question 1
