Math Squad

↳ To Infinity and Beyond. Introduction

↳ Review of Set Theory

↳ Functions

↳ Countability

↳ Cardinality

↳ Hilbert's Grand Hotel

Cardinality

The cardinality of a set is the number of elements in the set. Or rather it is a measure of the number of elements in the set because you cannot really put a number on the size of an infinite set but you could compare the size of two infinite sets based on their cardinality.

When Georg Cantor imagined that there were different sizes of infinity, the key to comparing those sizes rested in the cardinality of the sets.

For example, let $ A $ and $ B $ be two sets

Case 1: $ |A| = |B| $
$ |A| $ and $ |B| $ have the same cardinality if there exists a bijection from $ |A| $ to $ |B| $. In other words, there is a one-to-one mapping from $ |A| $ onto $ |B| $.
The intervals $ X = [-2,2] $ and $ Y = [4,10] $ have the same cardinality because there exists a bijective function where
$ y = \frac{3x}{2} + 7, \quad x \in X, y \in Y $
By this definition, the set of the set of rational numbers, the set of integers, and the set of even numbers are all the same size as the set of natural numbers since we have shown in the section on countability that there the elements of the respective sets can be put in some well-ordered correspondence with the natural numbers. Note also that finite sets with the same number of elements have the same cardinality.

Case 2: $ |A| $ ≤ $ |B| $
$ A $ has cardinality greater than or equal to the cardinality of $ B $ if there exists an injective (one-to-one) function from $ B $ to $ A $.

Fig 1: An injective, non-surjective mapping from $ X $ to $ Y $

Case 3: $ |A|>|B| $
A has cardinality strictly greater than the cardinality of B if there is an injective function, but no bijective function, from B to A.
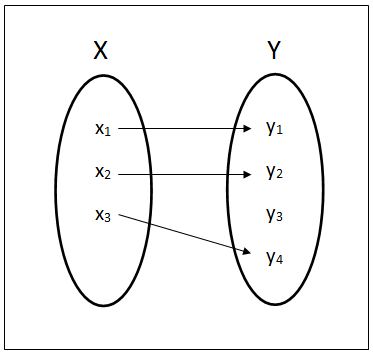
Figure 1 shows two sets $ X $ and $ Y $. The mapping from X to Y is one-to-one but not onto. Notice that the cardinality of $ Y $ is also greater.
It was shown in the section on countability, that the set R of all real numbers has cardinality strictly greater than the cardinality of the set N of all natural numbers. Similarly, the cardinality of the set of irrational numbers is strictly greater than that of the set of natural numbers.

Aleph Numbers

The different infinities can be ordered in terms of their cardinalities. Aleph numbers or the cardinal numbers are a sequence of numbers used to represent the size of infinite sets. The cardinalities of inifinite sets are denotes as follows:
$ \aleph_0 < \aleph_1 < \aleph_2 <... <\aleph_{\alpha}<... $
where $ \alpha $ ∈ N. ℵ$ _0 $ is the smallest infinity. All sets with smaller cardinalities are finite. All sets in bijection with the set of natural numbers have cardinality ℵ$ _0 $. ℵ$ _1 $ is the next largest infinity and so on. Any set with cardinality ℵ$ _1 $ or greater is countably infinite.

References

• R. Kenney. MA 301. "An Introduction to Proof through Real Analysis", Lecture Notes. Faculty of the Department of Mathematics, Purdue University, Spring 2012.

• J. J. Wanko in Vol. 102, No. 7. "Mathematics Teacher" March 2009.

• E. W. Weisstein. "Aleph-1." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Aleph-1.html. May 8th, 2013. [May 19th, 2013].

Questions and comments

If you have any questions, comments, etc. please post them below:

• Comment / question 1

Back to Math Squad page