The Hilbert Paradox

When Georg Cantor published his work on set theory and the nature of infinity, he faced opposition from many mathematicians such as Leopold Kronecker and Henri Poincaré. Fortunately for Cantor, another leading mathematician of the time, David Hilbert, came to his aid. Hilbert devised the metaphor of the infinite hotel to illustrate the beauty of Cantor's development of the concept of cardinality as it pertains to the infinite.
In Hilbert's paradox, there exists a grand hotel with infinitely many rooms and infinitely many guests. The hotel is named Hotel Infinity. It would appear that the hotel has no vacancies but can it accommodate a new guest? After all the infinite number of guests in the hotel plus one new guest is still an infinite number of guests. It would be unethical for the hotel to call itself the Hotel Infinity if it cannot in fact house an infinite number of guests.

The following video describes the problem in more detail.

Finitely Many New Guests

As seen in the video, Hotel Infinity does live up to its name. The video covers two scenarios. In the first, one new guest requests a room. All existing guests are asked to move one room over to accommodate him. In general any finite number of new guests can be accommodated. If $$ n $$ new guests arrive, current guests can be asked to move $$ n $$ rooms over to accommodate them.

Infinitely Many New Guests

In the second scenario in the video, a bus with an finite number of guests arrive. Even then, the hotel can still accommodate all guests. Note that in this paradox, we are dealing with natural numbers only. There are no negative rooms, neither are there any fractions of a room. The same goes for the guests. In general, any function that maps N → N will solve this problem. The video mentions the mapping $$ f(n) = 2n $$ .

Prime Numbers
In the second scenario in the video, a bus with an finite number of guests arrive. One solution for accommodating them is to ask existing guests in room $$ n+1 $$ , $$ n $$ ∈ N, to move to the $$ n $$ th prime numbered room since the prime numbers form a countably infinite set. So guests in rooms 1, 2 and 3 stay put, the guest from room 4 moves to room 5, the one from 5 moves to 7, 6 moves to 11, and so on. This generates an infinite number of vacancies for new guests. There will still be vacancies between prime numbers greater than 7.

Even Numbers
The above method is not as ergonomic as the one mentioned in the video where the guest in room $$ n $$ are asked to move to $$ 2n $$ . Now an infinite number of odd numbered rooms are available for the guests in the bus to occupy. Once this is done, the hotel once again has no vacancies.

Infinitely Many Buses, each with Infinitely Many New Guests

What if an infinite number of buses show up, each carrying an infinite number of passengers? Will the hotel be able to fit them in somehow? It turns out that it is possible to accommodate countably infinitely many bus-loads full of passengers and thankfully the number of buses is countably infinite since buses only come in natural numbers (no fractional or negative buses). In general, any pairing function such that N $$ X $$ N → N can be used to solve the problem. There are a number of ways to go about it. A few of them have been presented below.

Prime Powers Method
Odd numbered rooms are emptied and their tenants are sent to room $$ 2n $$ . Passengers from the first bus are assigned to rooms $$ 3^n, n = 1, 2, 3,... $$ . The second bus load of passengers are assigned rooms $$ 5^n $$ and so on. So passengers from bus number $$ m $$ are assigned room number $$ p^n $$ where $$ m,n $$ ∈ N and $$ p $$ is the $(m+1)^{th}$ prime number. This method leaves certain rooms vacant similar to the first method used to assign rooms to one bus load of new passengers.

Interleaving Method
Let $$ b $$ be the index number of the bus.
Let $$ b = 0 $$ for the existing guests of the hotel.
let $$ n $$ be the passenger number for the $b^{th}$ bus.
So for the $14^{th}$ passenger on bus $$ 23 $$ , $$ b=23 $$ and $$ n = 14 $$ . Now, if either number $$ b $$ or $$ n $$ is shorter, add leading zeros to the shorter number until both have the same number of digits. So if $$ n = 32 $$ and $$ b = 567 $$ , pad $$ n $$ wit zeros so we have that $$ n = 032 $$ .
Finally, interleave the digits of the two numbers to produce a new number. For example the old guest in room $$ 45 $$ has $$ n = 45 $$ and $$ b = 00 $$ . His/her new room becomes $$ 0405 $$ or $$ 405 $$ . Passenger $$ 12 $$ from bus number $$ 8902 $$ is assigned to room $$ 80900122 $$ . You must be careful to be consistent with your interleaving. I have used the method of $$ b_1n_1b_2n_2... $$ . You could use $$ n_1b_1b_2n_2... $$ as long as you are consistent throughout. Otherwise you could accidentally assign different guests the same room.
Unlike the prime powers method, the interleaving method fills the hotel completely.

Rational Numbers Method
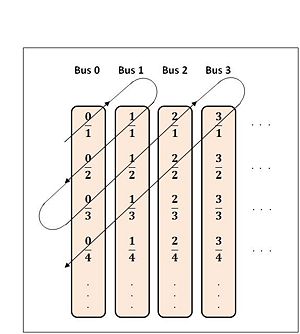
The solution is very similar to Cantor's diagonal ordering of rational numbers. The diagram is shown again in figure 1.

Fig 1: A system for passengers to disembark from the buses

Assume that the numerators correspond to the bus number and the denominators are the seat numbers on a bus. Assign bus number $$ 0 $$ to the guests already inside the hotel. So the fraction $$ 12/35 $$ is the $35^{th}$ passenger from the $12^{th}$ bus. In this way we can list all the passengers in an ordered fashion. Recall that in a previous section, $$ 4/2 $$ was equivalent to $$ 2/1 $$ but in this case they are two unique passengers from different buses. So now we can finally assign them rooms. If reception asks all the passengers from bus $$ 1 $$ to enter first, they will never get to the second bus and if they ask the first person from each bus to to enter first, they will never get to the second passenger. The solution is to follow Cantor's diagonal method for counting rational numbers.

References

J. J. Wanko in Vol. 102, No. 7. "Mathematics Teacher" March 2009.

"Hilbert's Infinite Hotel - 60-Second Adventures in Thought" Youtube link: http://www.youtube.com/watch?v=faQBrAQ87l4, Oct 3, 2011. [May 20th, 2013].

R. Kenney. MA 301. "An Introduction to Proof through Real Analysis", Lecture Notes. Faculty of the Department of Mathematics, Purdue University, Spring 2012.

Questions and comments

If you have any questions, comments, etc. please post them below:

Comment / question 1

Back to Math Squad page

Math Squad infinity Hilbert hotel mhossain S13 - Rhea

Contents