Math Squad

↳ To Infinity and Beyond. Introduction

↳ Review of Set Theory

↳ Functions

↳ Countability

↳ Cardinality

↳ Hilbert's Grand Hotel

Countability

When we count the elements of a set, we usually list them as element one, two, three, and so on until all the elements have been listed. Essentially, we are creating a bijective mapping of a portion of the set of natural numbers to the elements of the set. If the set is such that the counting does not end, such as the set of natural numbers itself, then what we have on our hands is an infinite set.

Definition

(a) An infinite set $ S $ is said to be denumerable (or countably infinite) if there exist a bijection of the set of natural numbers onto $ S $.
(b) A set $ S $ is said to be countable if it is either finite or denumerable.
(c) A set $ S $ is said to be uncountable if it is not countable.

So what the definition is telling us is that a set is countable if all its elements can be put in a one-to-one correspondence with the natural numbers (or a subset of the natural numbers for finite sets).

All finite sets are countable.

An infinite set $ A $ is countable if there is a one-to-one function whose domain is the set of natural numbers and whose range is $ A $.

Let us attempt a few exercises in detecting uncountable sets.

Even and Odd Numbers

Given that $ E $ is the infinite set of all even natural numbers, we have that

$ E := \{2n:n \in \mathbb{N} \} $

So we see that $ E $ is denumerable since the mapping of $ f: $ N → $ E $ defined by $ f(n) := 2n $ where $ n $ ∈ N, is a bijection of N onto $ E $.

Similarly, we could prove that the set $ O :=\{2n - 1 : n $ ∈ N} of odd numbers is denumerable.

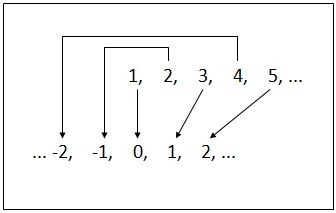
The Set of All Integers

You can see one way of matching integers to whole numbers in figure one so that there is a one-to-one correspondence between them. This makes Z, the set of all integers, a countably infinite set.

Fig 1: One-to-one correspondence between the natural numbers and the integers

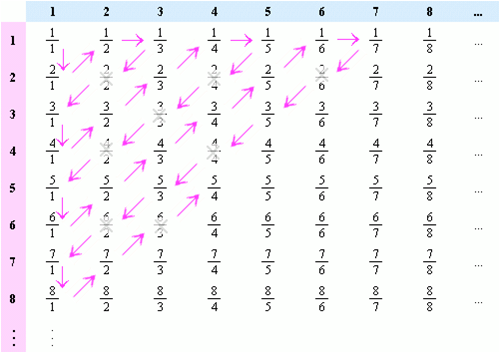
The Set of all Rational Numbers

Fig 2: Cantor's ordering of the rational numbers

Figure 2 shows Georg Cantor's diagonal argument for the rationals being countable. This is only an informal proof because the bijection is not defined precisely. His argument is essentially that the positive rational numbers can be placed in an array and counted in a ordered manner so that all of them are accounted for. Starting in the upper left corner and winding back and forth along each diagonal, a sequence is formed in which each element has a specific location. The duplicate elements in the sequence can be removed; these are shown in figure 2 as the ones that are crossed out. Similarly, the set of all negative rational numbers is also countable. We know that
$ \mathbb{Q} = \mathbb{Q}^- \cup \{0\} \cup \mathbb{Q}^+ $
Since the union of countable sets is countable, we conclude that the rationals form a countably infinite set. We will return to this method of ordering the rationals to solve the Hilbert paradox of the Grand Hotel in a later section.

Another method to prove that the rationals are countable is to define the height of a rational number $ p/q $ as $ |p|+q $. Then we can list all the rational number as follows:

Height 1: 0/1
Height 2: -1/1, 0/2, 1/1
Height 3: -2/1, -1/2, 0/3, 1/2, 2/1
Height 4: -3/1, -2/2, -1/3, 0/4, 1/3, 2/2, 3/1
$ \vdots $

We see that each row is countable, in fact they are finite, and there are countably many rows. So we have just expressed the rationals as a countable union of countable sets. The result is yet another countable set. The above list contains many duplicates but a subset of a countable set is also countable so this is not an issue as we saw in the diagonal procedure.

The Set of Real Numbers

So far we have only seen countable sets in this tutorial. Cantor proved in 1874 that the set of real numbers is countably infinite. He later published another proof for the same argument. Both methods have been presented here.

The first method uses the Nested Interval Property. If you are unfamiliar with this property, it will be helpful to know the following:

a. the closed interval $ [a,b] $ is a set of real numbers with the property that any number between $ a $ and $ b $ is also included in the set. i.e.
$ [a,b] := \{x \in \mathbb{R} : a\leq x \leq b\} $

b. Nested Interval Property If $ I_n = [a_n,b_n], n $ ∈ N, is a nested sequence of closed bounded intervals, then there exists a number ξ ∈ R such that ξ ∈ $ I_n $ for all n ∈ N.

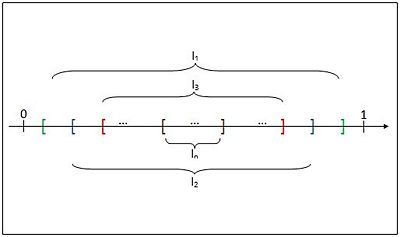
Now for our proof, we will show by contradiction that the unit interval $ [0,1] $ is an uncountable set. This strategy will suffice since if R were countable, its subset $ I $ would also be countable.

Fig 3: Nested sequence of closed intervals on $ [0,1] $

We begin by assuming that $ I $ is countable, then we can list the elements of the set as $ I := \{x_1, x_2, x_3, ..., x_n\} $. Let us select a closed interval $ I_1 $ of $ I $ such that $ x_1 $ ∉ $ I_1 $, then select a closed subinterval $ I_2 $ of $ I_1 $ such that $ x_2 $ ∉ $ I_2 $, and so on. In this way, we obtain a sequence of nonempty closed intervals
$ I_1 \supseteq I_2 \supseteq ... \supseteq I_n \supseteq ... $
such that $ I_n $ ⊆ $ I $ and $ x_n $ ∉ $ I_n $ for all $ n $. Therefore ξ ≠ $ x_n $ for all $ n $ ∈ N, but it must, otherwise the nested interval property is contradicted and if so, then the enumeration of $ I $ is an incomplete list of the elements of $ I $. So our initial assumption of the countability of $ I $ must be wrong. $ I $ cannot be a countable set so it is uncountable and so is R.

The second proof is also by contradiction based on decimal representation of real numbers. We start once again by assuming that $ I $ is countable. We use the fact that every real number $ x $ ∈ $ [0,1] $ has a decimal representation $ x = 0.b1_1b_2b_3... $, where $ b_i = 0,1,...,9 $. Suppose that there is an enumeration $ x_1,x_2,x_3,... $ of numbers in $ [0,1] $, such that
$ x_1 = 0.b_{11}b_{12}b_{13}...b_{1n}... $
$ x_2 = 0.b_{21}b_{22}b_{13}...b_{2n}... $
$ x_3 = 0.b_{31}b_{32}b_{33}...b_{3n}... $
$ \vdots $
$ x_n = 0.b_{n1}b_{n2}b_{13}...b_{nn}... $
$ \vdots $
Let s define a real number $ y:=0.y_1y_2y_3...y_n... $ by setting $ y_1:=2 $ if $ b_{11} $ ≥ $ 5 $ and $ y_1:=7 $ if $ b_{11} $ ≥ $ 4 $. i.e.
$ y_1 = \begin{cases} 2 & b_{nn}\geq 5 \\ 7 & b_{nn}\leq 4 \end{cases} $

Then $ y $ ∈ $ [0,1] $. Note that $ y $ is not equal to any of the numbers with two decimal representations, since $ y_n $ ≠ $ 0,9 $ for all $ n $ ∈ N. Furhter, since $ x_n $ and $ y $ differ in the $ n $th decimal place, then $ y $ ≠ $ x_n $ for any $ n $ ∈ N. Therefore, $ y $ is not included in the enumeration of $ [0,1] $, contradicting the hypothesis. So both $ I $ and R must be uncountable.

The fact that the set or real numbers is countable can be combined with the fact that the set of rationals is countable to conclude that the irrationals are uncountable since the set of irrational numbers is given by R\Q.

The countability of a set is important in understanding the concept of cardinality. As mentioned before, this is a key idea that is essential for comprehending the nature of the infinite.

References

• R. G. Bartle, D. R. Sherbert, "Preliminaries" in "An Introduction to Real Analysis", Third Edition, John Wiley and Sons Inc. 2000 ch. 1, sect. 1.1, pp 16-18.

• R. G. Bartle, D. R. Sherbert, "The Real Numbers" in "An Introduction to Real Analysis", Third Edition, John Wiley and Sons Inc. 2000 ch. 2, sect. 2.5, pp 47-50.

• R. Kenney. MA 301. "An Introduction to Proof through Real Analysis", Lecture Notes. Faculty of the Department of Mathematics, Purdue University, Spring 2012.

• J. J. Wanko in Vol. 102, No. 7. "Mathematics Teacher" March 2009.

Questions and comments

If you have any questions, comments, etc. please post them below:

• Comment / question 1

Back to Math Squad page