(New page: Category:ECE637 Category:sLecture Category:image processing Category:lecture notes sLecture :↳ [[ECE637_to...) |
|||
| Line 40: | Line 40: | ||
---- | ---- | ||
| − | == | + | ==Definition== |
| + | Let <br/> | ||
| + | <math>\begin{align} | ||
| + | P_{\theta}(\rho) &= CTFT \{p_\theta(r)\} \\ | ||
| + | F(u,v) &= CSFT\{f(x,y)\} | ||
| + | \end{align}</math> | ||
| − | [[Image: | + | where <math>\rho</math> is the frequency variable corresponding to <math>r</math> just as <math>u</math> and <math>v</math> are the frequency variables corresponding to <math>x</math> and <math>y</math> respectively. |
| + | |||
| + | Then<br/> | ||
| + | <math>P_{\theta}(\rho) = F(\rho\cos(\theta),\rho\sin(\theta)) \ </math> | ||
| + | |||
| + | Recall that <math>p_{\theta}(r)</math> is the projection of image <math>f(x,y)</math> at angle <math>\theta</math>. <math>P_{\theta}(\rho)</math> is its 1-D Fourier transform. <math>F(u,v)</math> on the other hand, is the 2-D Fourier transform of image <math>f(x,y)</math>. | ||
| + | |||
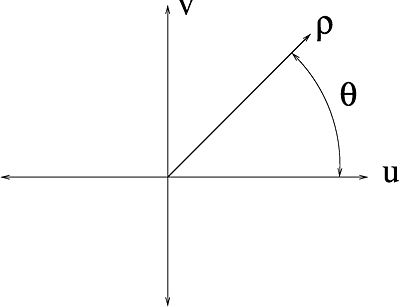
| + | So essentially, the theorem tells us that <math>P_{\theta}(\rho)</math> is <math>F(u,v)</math> in polar coordinates. | ||
| + | |||
| + | [[Image:FST_fig1_mh.jpeg|400px|thumb|left|Fig 1: <math>P_{\theta}(\rho)</math> is <math>F(u,v)</math> in polar coordinates]] | ||
| + | |||
| + | |||
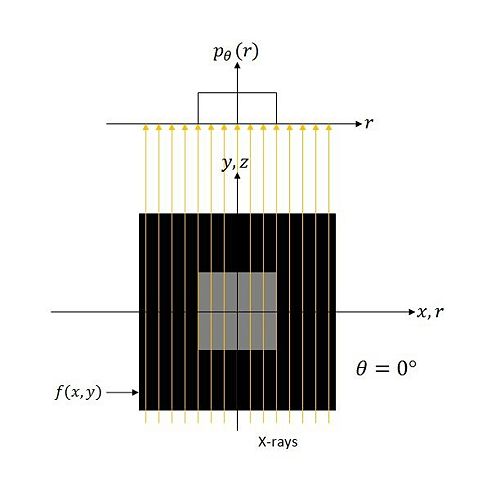
| + | Let us look at the simple example in figure 2 to illustrate this relationship. For the given <math>f(x,y)</math>, the projection for <math>\theta = 0</math>° is a 1-D rect function. Let us assume it is of unit area. <br/> | ||
| + | [[Image:FST_fig2_mh.jpeg|500px|thumb|left|Fig 2: <math>p_{\theta}(r)</math> at angle <math>\theta = 0</math>°]] | ||
| + | |||
| + | |||
| + | So we have that <br/> | ||
| + | <math>\begin{align} | ||
| + | p_{\theta}(r) |_{\theta = 0} &= rect(r) \\ | ||
| + | \Rightarrow P_{\theta}(\rho) |_{\theta = 0} &= CTFT\{p_{\theta}(r) \}|_{\theta = 0} \\ | ||
| + | &= sinc(\rho) | ||
| + | \end{align}</math> | ||
| + | |||
| + | But <math>f(x,y)</math> is a 2-D rect so<br/> | ||
| + | <math>\begin{align} | ||
| + | f(x,y) &= rect(x)rect(y) \\ | ||
| + | \Rightarrow F(u,v) &= CSFT\{f(x,y)\} \\ | ||
| + | &= sinc(u)sinc(v) | ||
| + | \end{align}</math> | ||
| + | |||
| + | Now lets convert <math>F</math> from cartesian coordinates <math>u,v</math> to polar coordinates <math>(\rho,\theta)</math> where <math>\theta = 0</math>°<br/> | ||
| + | <math>\begin{align} | ||
| + | F(u,v) &= sinc(u)sinc(v) \\ | ||
| + | &= sinc(\rho \cos\theta)sinc(\rho \sin\theta)|_{\theta = 0} \\ | ||
| + | &= sinc(\rho) \\ | ||
| + | &= P_{\theta}(\rho)|_{\theta = 0} | ||
| + | \end{align}</math> | ||
| + | |||
| + | So we see that the theorem holds for the above scenario. But it does not prove the theorem, only verifies it for a particular situation. The theorem can be proved in different ways. Two of the methods are presented below. | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == Proof == | ||
| + | |||
| + | === Method 1 === | ||
| + | |||
| + | The first method relies on plugging variable substitutions into the defintion. | ||
| + | |||
| + | By definition, <br/> | ||
| + | <math>\begin{align} | ||
| + | P_{\theta}(\rho) &= CTFT\{p_{\theta}(r)\} \\ | ||
| + | &= \int_{-\infty}^{\infty}p_{\theta}(r)e^{-j2\pi\rho r}dr \\ | ||
| + | &=\int_{-\infty}^{\infty} [\int_{-\infty}^{\infty}f(\mathbf{A_{\theta}} | ||
| + | \begin{bmatrix} | ||
| + | r \\ | ||
| + | z | ||
| + | \end{bmatrix}) dz]e^{-j2\pi\rho r}dr \\ | ||
| + | &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(\mathbf{A_{\theta}} | ||
| + | \begin{bmatrix} | ||
| + | r \\ | ||
| + | z | ||
| + | \end{bmatrix})e^{-j2\pi\rho r}dzdr | ||
| + | \end{align}</math> | ||
| + | |||
| + | Next we make the following change of variables<br/> | ||
| + | <math>\begin{bmatrix} | ||
| + | r \\ | ||
| + | z | ||
| + | \end{bmatrix} = \mathbf{A_{-\theta}}\begin{bmatrix} | ||
| + | r \\ | ||
| + | z | ||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | Notice that the Jacobian is '''<math>|{A_{-\theta}}|</math>'''<math>=1</math> since <br/> | ||
| + | <math>\begin{align} | ||
| + | \frac{\partial (r,z)}{\partial (x,y)}| &= det \begin{bmatrix} | ||
| + | \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ | ||
| + | \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \end{bmatrix} \\ | ||
| + | &= det \begin{bmatrix} | ||
| + | \frac{\partial (x\cos(\theta)+y\sin(\theta))}{\partial x} & \frac{\partial (x\cos(\theta)+y\sin(\theta))}{\partial y} \\ | ||
| + | \frac{\partial (-x\sin(\theta)+y\cos(\theta))}{\partial x} & \frac{\partial (-x\sin(\theta)+y\cos(\theta))}{\partial y} \end{bmatrix} \\ | ||
| + | &= det \begin{bmatrix} \cos\theta & \sin\theta \\ | ||
| + | -\sin\theta & \cos\theta \end{bmatrix} \\ | ||
| + | &= \cos^2\theta + \sin^2\theta \\ | ||
| + | &=1 | ||
| + | \end{align}</math> | ||
| + | |||
| + | Then,<br/> | ||
| + | <math> drdz = |\frac{\partial(r,z)}{\partial(x,y)}|dxdy = dxdy</math> | ||
| + | |||
| + | Also notice that <math>r=x\cos(\theta)+y\sin(\theta)</math>. So finally we have that <br/> | ||
| + | <math>\begin{align} | ||
| + | P_{\theta}(\rho) &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y)e^{-j2\pi\rho[x\cos(\theta)+y\sin(\theta)]}dxdy \\ | ||
| + | &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y)e^{-j2\pi[x\rho\cos(\theta)+y\rho\sin(\theta)]}dxdy \\ | ||
| + | &= F(\rho\cos(\theta),\rho\sin(\theta))_{\blacksquare} | ||
| + | \end{align}</math> | ||
| + | |||
| + | |||
| + | === Method 2 === | ||
| + | |||
| + | The second method is slightly more compact than the first. | ||
| + | |||
| + | First, let <math>\theta = 0</math>, then<br/> | ||
| + | <math>\begin{align} | ||
| + | p_0(r) &= \int_{-\infty}^{\infty}f(r,y)dy \\ | ||
| + | \Rightarrow P_0(\rho) &= \int_{-\infty}^{\infty}p_0(r)e^{-2\pi jr\rho}dr \\ | ||
| + | &= \int_{-\infty}^{\infty}[\int_{-\infty}^{\infty}f(r,y)dy]e^{-2\pi jr\rho}dr \\ | ||
| + | &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(r,y)e^{(-2\pi j(r\rho+y0)}drdy \\ | ||
| + | &= F(\rho,0) | ||
| + | \end{align}</math> | ||
| + | |||
| + | By the rotation property of the CSFT, it must hold for any <math>\theta</math>. | ||
Revision as of 15:20, 26 May 2013
- ↳ Topic 2: Tomographic Reconstruction
- ↳ Intro
- ↳ CT
- ↳ PET
- ↳ Co-ordinate Rotation
- ↳ Radon Transform
- ↳ Fourier Slice Theorem
The Bouman Lectures on Image Processing
A sLecture by Maliha Hossain
Subtopic 3: Fourier Slice Theorem
© 2013
Contents
Excerpt from Prof. Bouman's Lecture
Accompanying Lecture Notes
Definition
Let
$ \begin{align} P_{\theta}(\rho) &= CTFT \{p_\theta(r)\} \\ F(u,v) &= CSFT\{f(x,y)\} \end{align} $
where $ \rho $ is the frequency variable corresponding to $ r $ just as $ u $ and $ v $ are the frequency variables corresponding to $ x $ and $ y $ respectively.
Then
$ P_{\theta}(\rho) = F(\rho\cos(\theta),\rho\sin(\theta)) \ $
Recall that $ p_{\theta}(r) $ is the projection of image $ f(x,y) $ at angle $ \theta $. $ P_{\theta}(\rho) $ is its 1-D Fourier transform. $ F(u,v) $ on the other hand, is the 2-D Fourier transform of image $ f(x,y) $.
So essentially, the theorem tells us that $ P_{\theta}(\rho) $ is $ F(u,v) $ in polar coordinates.
Let us look at the simple example in figure 2 to illustrate this relationship. For the given $ f(x,y) $, the projection for $ \theta = 0 $° is a 1-D rect function. Let us assume it is of unit area.
So we have that
$ \begin{align} p_{\theta}(r) |_{\theta = 0} &= rect(r) \\ \Rightarrow P_{\theta}(\rho) |_{\theta = 0} &= CTFT\{p_{\theta}(r) \}|_{\theta = 0} \\ &= sinc(\rho) \end{align} $
But $ f(x,y) $ is a 2-D rect so
$ \begin{align} f(x,y) &= rect(x)rect(y) \\ \Rightarrow F(u,v) &= CSFT\{f(x,y)\} \\ &= sinc(u)sinc(v) \end{align} $
Now lets convert $ F $ from cartesian coordinates $ u,v $ to polar coordinates $ (\rho,\theta) $ where $ \theta = 0 $°
$ \begin{align} F(u,v) &= sinc(u)sinc(v) \\ &= sinc(\rho \cos\theta)sinc(\rho \sin\theta)|_{\theta = 0} \\ &= sinc(\rho) \\ &= P_{\theta}(\rho)|_{\theta = 0} \end{align} $
So we see that the theorem holds for the above scenario. But it does not prove the theorem, only verifies it for a particular situation. The theorem can be proved in different ways. Two of the methods are presented below.
Proof
Method 1
The first method relies on plugging variable substitutions into the defintion.
By definition,
$ \begin{align} P_{\theta}(\rho) &= CTFT\{p_{\theta}(r)\} \\ &= \int_{-\infty}^{\infty}p_{\theta}(r)e^{-j2\pi\rho r}dr \\ &=\int_{-\infty}^{\infty} [\int_{-\infty}^{\infty}f(\mathbf{A_{\theta}} \begin{bmatrix} r \\ z \end{bmatrix}) dz]e^{-j2\pi\rho r}dr \\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}f(\mathbf{A_{\theta}} \begin{bmatrix} r \\ z \end{bmatrix})e^{-j2\pi\rho r}dzdr \end{align} $
Next we make the following change of variables
$ \begin{bmatrix} r \\ z \end{bmatrix} = \mathbf{A_{-\theta}}\begin{bmatrix} r \\ z \end{bmatrix} $
Notice that the Jacobian is $ |{A_{-\theta}}| $$ =1 $ since
$ \begin{align} \frac{\partial (r,z)}{\partial (x,y)}| &= det \begin{bmatrix} \frac{\partial r}{\partial x} & \frac{\partial r}{\partial y} \\ \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \end{bmatrix} \\ &= det \begin{bmatrix} \frac{\partial (x\cos(\theta)+y\sin(\theta))}{\partial x} & \frac{\partial (x\cos(\theta)+y\sin(\theta))}{\partial y} \\ \frac{\partial (-x\sin(\theta)+y\cos(\theta))}{\partial x} & \frac{\partial (-x\sin(\theta)+y\cos(\theta))}{\partial y} \end{bmatrix} \\ &= det \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \\ &= \cos^2\theta + \sin^2\theta \\ &=1 \end{align} $
Then,
$ drdz = |\frac{\partial(r,z)}{\partial(x,y)}|dxdy = dxdy $
Also notice that $ r=x\cos(\theta)+y\sin(\theta) $. So finally we have that
$ \begin{align} P_{\theta}(\rho) &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y)e^{-j2\pi\rho[x\cos(\theta)+y\sin(\theta)]}dxdy \\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y)e^{-j2\pi[x\rho\cos(\theta)+y\rho\sin(\theta)]}dxdy \\ &= F(\rho\cos(\theta),\rho\sin(\theta))_{\blacksquare} \end{align} $
Method 2
The second method is slightly more compact than the first.
First, let $ \theta = 0 $, then
$ \begin{align} p_0(r) &= \int_{-\infty}^{\infty}f(r,y)dy \\ \Rightarrow P_0(\rho) &= \int_{-\infty}^{\infty}p_0(r)e^{-2\pi jr\rho}dr \\ &= \int_{-\infty}^{\infty}[\int_{-\infty}^{\infty}f(r,y)dy]e^{-2\pi jr\rho}dr \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(r,y)e^{(-2\pi j(r\rho+y0)}drdy \\ &= F(\rho,0) \end{align} $
By the rotation property of the CSFT, it must hold for any $ \theta $.
References
- C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.
Questions and comments
If you have any questions, comments, etc. please post them on this page
Back to the "Bouman Lectures on Image Processing" by Maliha Hossain