- ↳ Topic 2: Tomographic Reconstruction
- ↳ Intro
- ↳ CT
- ↳ PET
- ↳ Co-ordinate Rotation
- ↳ Radon Transform
- ↳ Fourier Slice Theorem
- ↳ Convolution Back Projection
The Bouman Lectures on Image Processing
A Slecture by Maliha Hossain
Subtopic 4: Co-ordinate Rotation
© 2013
Contents
[hide]Excerpt from Prof. Bouman's Lecture
Accompanying Lecture Notes
To calculate the projections of the object as we scan it, we must calculate an integral known as the Radon Transform. Recall that the density of the object is given by the function $ f(x,y) $. We will see later in the next section that the integral must be calculated along a different axis. Therefore we must first perform a coordinate rotation in order to calculate this integral.
$ A_{\theta} $ is the orthogonal counterclockwise rotation matrix given by
$ \mathbf{A_{\theta}}=\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} $
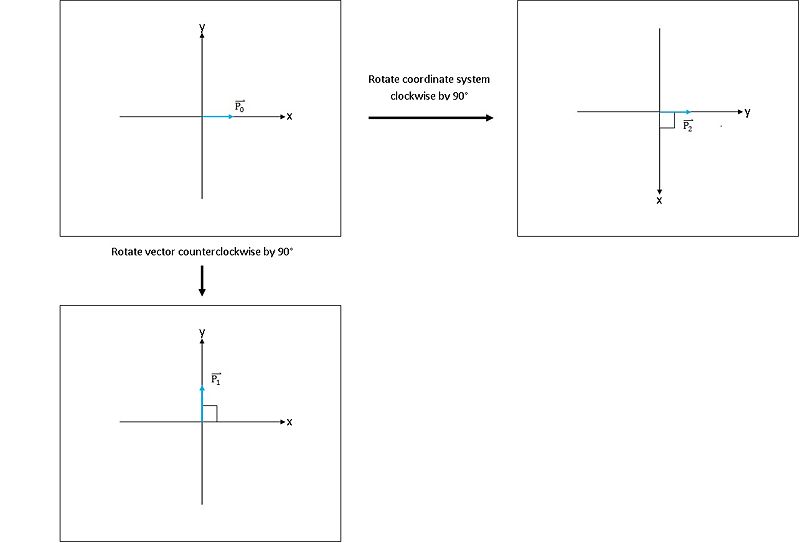
The matrix rotates vector $ {v_0} $ in a 2-dimensional real space by angle $ \theta $ in a fixed coordinate system. Notice that this is equivalent to keeping the vector fixed and rotating the coordinate system clockwise by $ \theta $. This equivalence is illustrated in figure 1.
Let $ {P_0} $ be the unit vector shown in the top left corner of figure 1.
$ \mathbf{P_0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} $
Rotating $ P_0 $ $ 90 $° counterclockwise produces the unit vector $ P_1 $ shown in the bottom left
$ \mathbf{P_1} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $
The result of rotating the coordinate axes clockwise by $ 90 $° is shown in the top right. We have that
$ \mathbf{P_2} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $
So we see that vectors $ P_1 $ and $ P_2 $ are equivalent. In other words, rotating a vector counterclockwise by angle $ \theta $ is the same as rotating the coordinate axes clockwise by angle $ \theta $.
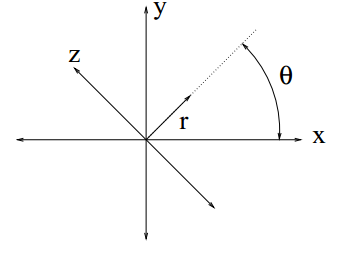
Let us define a new coordinate system $ (r,z) $ where
$ \begin{bmatrix} x \\ y \end{bmatrix} = \mathbf{A_{\theta}}\begin{bmatrix} r \\ z \end{bmatrix} $
i.e. vector $ [r,z]' $ is rotated counterclockwise angle $ \theta $ to produce vector $ [x,y]' $
Figure 2 shows the geometric interpretation of the rotation.
- Inverse Transformation
The rotation can be inverted by multiplying the rotated vector with matrix $ A_{-\theta} $, where
$ \mathbf{A_{-\theta}}=\begin{bmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{bmatrix} = \begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix} $
and we have that
$ \begin{bmatrix} r \\ z \end{bmatrix} = \mathbf{A_{-\theta}}\begin{bmatrix} x \\ y \end{bmatrix} $
Notice that rotating a vector counterclockwise by angle $ -\theta $ is the same as rotating the vector clockwise by angle $ \theta $. In fact, $ A_{-\theta} $ is the orthogonal clockwise rotation matrix. Since $ A_{\theta} $ is an orthogonal matrix, it's inverse is the same as its transpose, i.e.
$ \mathbf{A_{\theta}}^{-1} = \mathbf{A_{\theta}}^T = \begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix} = \mathbf{A_{-\theta}} $
The result is obvious since it is basically telling us that the action of rotating a point counterclockwise by angle $ \theta $ can be undone by rotating it clockwise by angle $ \theta $.
References
- C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.
- E. W. Weisstein, "Rotation Matrix." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RotationMatrix.html. May 8th, 2013 [May 21st, 2013]
Questions and comments
If you have any questions, comments, etc. please post them on this page
Back to the "Bouman Lectures on Image Processing" by Maliha Hossain