sLecture

↳ Topic 2: Tomographic Reconstruction

↳ Intro

↳ CT

↳ PET

↳ Co-ordinate Rotation

↳ Radon Transform

↳ Fourier Slice Theorem

↳ Convolution Back Projection

Excerpt from Prof. Bouman's Lecture

Accompanying Lecture Notes

The concept behind convolution back projection is that you drag the projections back through the image and sum them to obtain an approximation of the original image. We will see that star-shaped artifacts are introduced in the resulting image by this process. These artifacts can be reduced by filtering with a high pass filter prior to back-projection. For this reason, the process is also commonly referred to as Filtered Back Projection.

The method relies on the relationship dictated by the Fourier Slice Theorem. However you do not need to perform any calculations in the frequency domain using this method so it is computationally much faster and is the most commonly used method used in tomographic reconstruction.

Summary of CBP algorithm

1. Measure projections $ p_{\theta}(r) $.
2. Filter the projections to obtain $ g_{\theta}(r) = h(r)*p_{\theta}(r) $.
3. Back project filtered projections using the following
   

$ f(x,y) = \int_0^{\pi}g_{\theta}(x\cos(\theta)+x\sin(\theta))d\theta $

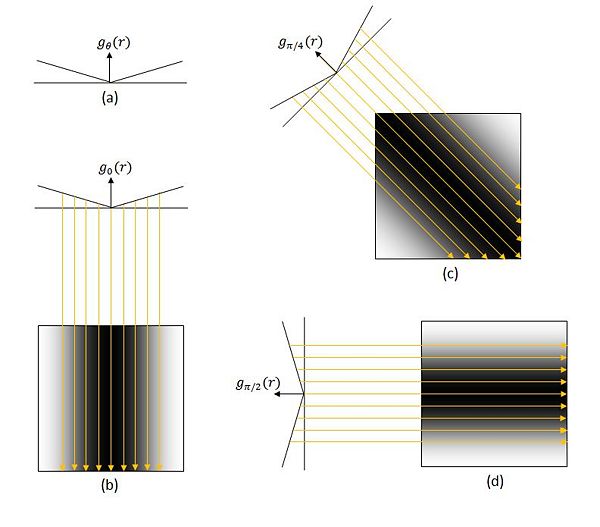
Figure 1 shows what it means to back project. If we assume that $ g_{theta} $ is the same function shown in (a) for all $ \theta $, we see that when you back project, it is like you are smearing the value of $ g_{theta}(r) $ across an image at angle $ \theta $. Another way to think about it is that you have a function in one variable, $ g_{\theta}(r) $ and you project that backwards to form a function in two variables, or an image where every slice through the image at angle $ \theta $ is equal to $ g_{\theta}(r) $.

Figure 1: (a) $ g_{\theta}(r) $ for all $ \theta $. (b) back projection for $ \theta =0 $°. (c) back projection for $ \theta = 45 $°. (d) back projection for $ \theta = 90 $°.(e) back projection for $ \theta = 135 $°.

So we see that back projection "smears" values of $ g(r) $ back over the image, and then adds smeared images for each angle. For the example in figure 1, you would add the back projections shown in (b), (c), (d) and (e) to obtain an approximation of the original image. The result is shown in (f). Theoretically, if I take an infinite number of filtered back projections, I can get perfect reconstruction of the original image given that the original is band limited. But of course this is not possible in practice. In general, if you have an $ n $ by $ n $ image, you need to perform roughly $ n $ or more back projections.

You can also see a more thorough illustration of tomographic reconstruction using CBP in Professor Bouman's MATLAB demo. The code is available here and the resulting images can be found here.

Derivation of the filter $ h(r) $

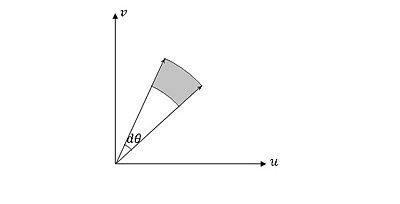
In order to compute the inverse CSFT of $ F(u,v) $ in polar coordinates, we must use the Jacobian of the polar coordinate transformation.
$ du dv = |\rho|d\theta d\rho \ $
where $ u = \rho\cos(\theta) $ and $ v = \rho\sin(\theta) $

This results in the expression
$ f(x,y) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(u,v)e^{2\pi j(xu+yv)}dudv $

Using the Fourier slice theorem, we can replace F(x,y) with its representation in polar coordinates, $ P_{\theta}(\rho) $
$ \begin{align} \Rightarrow f(x,y) &= \int_{-\infty}^{\infty}\int_0^{\pi}P_{\theta}(r)e^{2\pi j(x\rho\cos(\theta) +y\rho\sin(\theta))}dudv \\ &= \int_0^{\pi}\underbrace{[\int_{-\infty}^{\infty}|\rho|P_{\theta}e^{2\pi j\rho(x\cos(\theta) +y\sin(\theta))}d\rho]}_{g_{\theta}(x\cos(\theta) + y\sin(\theta))}d\theta \end{align} $

Then $ g_{\theta}(t) $ is given by
$ \begin{align} g_{\theta}(t) &= \int_{\infty}^{\infty}|\rho|P_{\theta}(\rho)e^{2\pi j\rho t}d\rho \\ &= CTFT^{-1}\{|\rho|P_{\theta}(\rho)\} \\ &= h(t) * p_{\theta}(r) \end{align} $

where $ h(t) = CTFT^{-1}\{|\rho|\} $, and
$ f(x,y) = \int_0^{\pi}g_{\theta}(x\cos(\theta) + y\sin(\theta))d\theta $

A closer look at Projection Filter

At each angle, projections are filtered to produce $ g){\theta}(r) $:
$ g_{\theta}(r) = h(r)*p_{\theta}(r) \ $.

The frequency response of the filter is given by
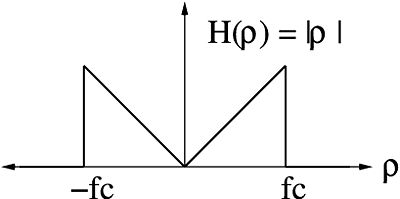
$ H(\rho) = |\rho| \ $
As you can see from figure 3, $ h(r) $ is like a high pass filter.

Fig 2: Frequency response of $ H(\rho) = |\rho| $

The frequency response depends on the absolute value of $ \rho $. Recall that $ \rho $ is the radial distance from the origin so this filter is essentially weighting the input by the magnitude of $ \rho $. This is because as you get further from the origin, the shaded area shown in figure 4 grows as $ \rho $ gets larger.

Fig 3: Area of a slice through circular rings.

The filter could theoretically have unlimited bandwidth but if the image is bandlimited, then the real filter does not need to have infinite bandwidth. The frequencies can be clipped at $ |\rho| $ ≤ $ f_c $ for some cutoff frequency $ f_c $.

The frequency response in figure 3 resembles a rect function minus a tri function. So
$ \begin{align} H(\rho) &= f_c[rect(f/(2f_c))-\wedge(f/f_c)] \\ h(r) &= f_c^2[2sinc(t2f_c)-sinc^2(tf_c)] \end{align} $

A Closer Look at Back Projection

Back projection function is given by
$ f(x,y) = \int_0^{\pi}b_{\theta}(x,y)d\theta $

where
$ b_{\theta}(x,y) = g_{\theta}(x\cos(\theta)+y\sin(\theta)) $

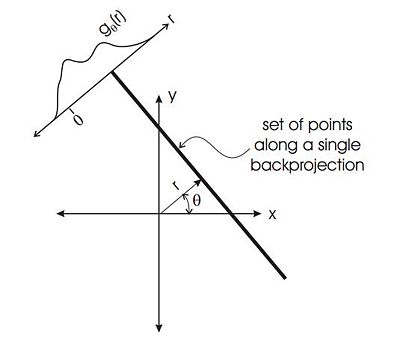
Consider the set of points $ (x,y) $ such that
$ r = x\cos(\theta)+y\sin(\theta) $

This set looks like

Fig 4: Graphical representation of the set $ \{(x,y):r=x\cos(\theta)+y\sin(\theta)\} $

Along this line, $ b_{\theta}(x,y) = g_{\theta}(r) $.

For each angle $ \theta $ the back projection is constant along the lines of angle $ \theta $ and take on value $ g_{\theta}(r) $. As stated earlier, this is basically like the adjoint of the forward projection operator. In the forward projection, you sum together all the quantities along the solid line shown in figure 5. In the back projection, you take a value from the projection and put it in each location in proportion to the weight you used to add it up in the first place so they are like transpose operations. The domain of the forward projection operator becomes the range of the back projection operator and vice versa.

Complete back projection is formed by integrating (summing) back projections for angles ranging from $ 0 $ to $ \pi $.
$ \begin{align} f(x,y) &= \int_0^{\pi}b_{\theta}(x,y)d\theta \\ &\approx \frac{\pi}{M} \sum_{m=0}^{M-1} b_{\frac{m\pi}{M}}(x,y) \end{align} $

References

• C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to the "Bouman Lectures on Image Processing" by Maliha Hossain