sLecture

↳ Topic 2: Tomographic Reconstruction

↳ Intro

↳ CT

↳ PET

↳ Co-ordinate Rotation

↳ Radon Transform

↳ Fourier Slice Theorem

↳ Convolution Back Projection

Excerpt from Prof. Bouman's Lecture

Accompanying Lecture Notes

Positron Emission Tomography, or PET, is a non invasive imaging technique that produces a three-dimensional representation of the body. It is commonly used in clinical oncology and is a functional medical imaging modality. It can also be used as a form of molecular imaging.

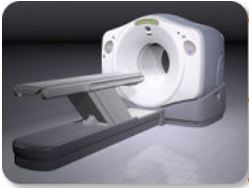
Figure 1 shows a PET scanner. It is very similar to a CT scanner in appearance but the underlying physics of the acquisition is quite different.

Fig 1: A PET scanner equipped with CT system

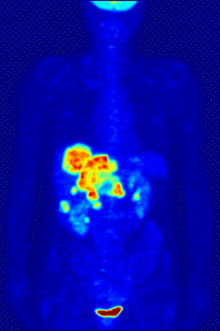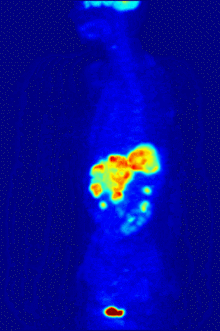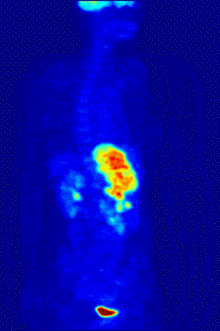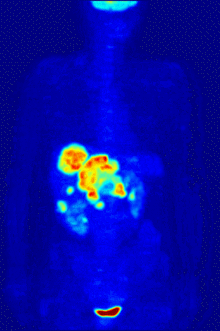
Prior to a PET a scan, the patient is injected with a positron emitting radio-tracer, typically Fluorodeoxyglucose (FDG). FDG is a glucose molecule where the fluorine atom is the radioactive isotope $ ^{18} $F sugar with a fluorine atom attached. $ ^{18} $F has a half-life of about 110 minutes. This is long enough for it to be produced in a cyclotron, combined with the sugar and transported to the hospital and still be detectable after the sugar has been injected. Since an atom's chemical behavior is largely determined by its electronic structure, different isotopes exhibit nearly identical chemical behavior. The body therefore metabolizes FDG like other as sugars. Cancerous cells metabolize more sugar at a higher rate because they tend to grow uncontrollably. A tumor will have a higher rate of uptake of the FDG than the surrounding healthy tissue and it will light up in the scan. The bladder and kidneys will also light up since they regulate and excrete sugars.

Fig 2: A full-body PET

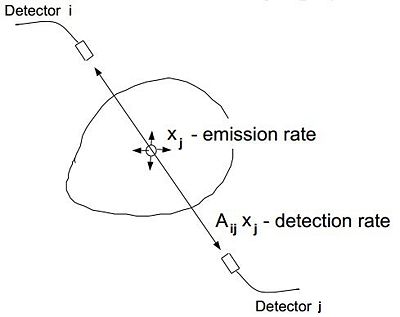
As the FDG in patients body is metabolized, the radioactive isotope may break down. As it decays, it produces a positron which annihilates a nearby electron. As a result of this annihilation, two gamma particles are released. As the positron and the electron had non zero momentum before the collision, the momentum of the two gamma particles are also non zero. The paths they traverse make an angle of about 179 degrees. So to summarize, as a result of the annihilation you have two gamma particles travelling at almost exactly opposite directions. The PET contains a ring of detectors (this ring is stationary whereas the detectors in a CT scanner rotate with the gantry). Each detector in a PET scanner counts photons. When it encounters photon, it registers the time of the scintillation. A photon travels about a foot (30 cm) in free space in a nano second. When two detectors detect a photon simultaneously or within a small window of time, we know that an event has occurred along the line connecting detectors. A ring of detectors can be used to measure all angles and displacements

So for example, let $ t_i $ and $ t_j $ be the time when detectors i and j in figure 3 register a scintillation. Since the cavity in the scanner is a few feet across, then we can assume that if $ |t_i-t_j| < 10 $ ns, the gamma particles detected resulted from the same annihilation. They are from the same coincident event.

Given that you have 512 detectors, you have 512(511)/2 virtual detectors. For every unique pair of detectors, you have a virtual detector and you could count how many annihilations occur along that detector and you get a line integral. So this is another technology where you the measurements are line integrals. Once you have obtained the projections, it boils down to the same inversion process as CT.

Fig 3: Event detection in a PET scanner

$ E[y_i] = \sum_j A_{ij}x_j \ $

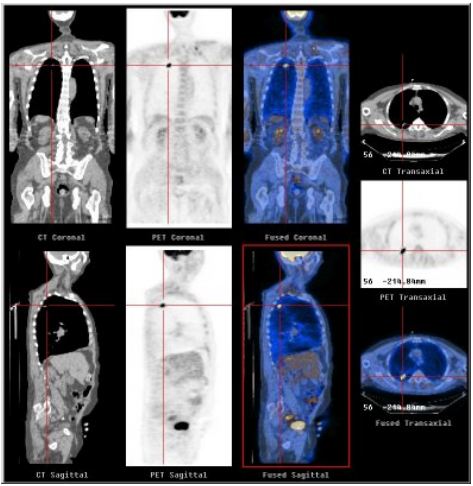
PET scanners are much more expensive than CT scanners. They also have relatively poor spatial and temporal resolution. Most PET systems are equipped with a CT scanner like the one shown in figure 1. Figure 4 shows a PET scan superimposed on a CT scan. This is much more helpful to radiologists in trying to diagnose diseases. You can see that there is very little anatomical detail in the stand alone PET scans in figures 2 and 4.

Fig 4: CT and PET scans (grey-scale) displayed on their own as well as superimposed on one another (images in blue)

References

• C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to the "Bouman Lectures on Image Processing" by Maliha Hossain