(→Partial Differential Equations (Continued): Fix transcription errors for this section.) |
|||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| + | =Lecture 28, [[ECE662]]: Decision Theory= | ||
| + | |||
| + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. | ||
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| + | |||
| + | ---- | ||
| + | ---- | ||
=The Last Class= | =The Last Class= | ||
| − | Welcome to the last class of the semester! The kiwi is going to be | + | Welcome to the last class of the semester! The [[About_Rhea|kiwi]] is going to be |
a great resource. | a great resource. | ||
| Line 15: | Line 52: | ||
| − | We may | + | We may discretize this using a finite difference equation. |
<center><math> | <center><math> | ||
| Line 45: | Line 82: | ||
e.g. in <math>\mathbb{R}^{2}</math>, consider the curve<center><math> | e.g. in <math>\mathbb{R}^{2}</math>, consider the curve<center><math> | ||
| − | \overrightarrow(\tau)=(x(\tau),y(\tau))</math></center> | + | \overrightarrow{\tau}(\tau)=(x(\tau),y(\tau))</math></center> |
| − | We shall | + | We shall commonly drop the vector notation in the rest of this discussion. |
[Figure: Arbitrary curve , looping from <math>\tau=0</math> to <math>\tau=10,000</math>.] | [Figure: Arbitrary curve , looping from <math>\tau=0</math> to <math>\tau=10,000</math>.] | ||
| Line 60: | Line 97: | ||
<center><math> | <center><math> | ||
\frac{dc}{dt}=\frac{d^{2}c}{d\tau^{2}}</math></center> | \frac{dc}{dt}=\frac{d^{2}c}{d\tau^{2}}</math></center> | ||
| − | |||
This gives us two 1-D heat equations | This gives us two 1-D heat equations | ||
| Line 80: | Line 116: | ||
| − | If we cannot solve these analytically, we can again | + | If we cannot solve these analytically, we can again discretize the |
solution. | solution. | ||
| Line 104: | Line 140: | ||
[Figure showing the notation] | [Figure showing the notation] | ||
| − | [ | + | At this point in the class, we reviewed how to [[Solving differential equations iteratively_Old Kiwi|solve differential equations iteratively]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
=How does this apply to valley-finding?= | =How does this apply to valley-finding?= | ||
| Line 157: | Line 176: | ||
| − | + | [Figure of density points and approximated density landscape.] | |
| − | + | [Start with curve around both mountains, this is the initial guess | |
for the boundaries of the feature space] | for the boundaries of the feature space] | ||
| − | + | [Note that the curve is discritized, each point is assigned to a | |
different value of <math>\tau</math>] | different value of <math>\tau</math>] | ||
| Line 184: | Line 203: | ||
*We must fix the number of clusters | *We must fix the number of clusters | ||
| − | *We must assume the curve has some degree of smoothness. | + | *We must assume the curve has some degree of smoothness. |
| − | *The points tend to collapse on each other or move away from each other. | + | [Figure of this phenomenon] |
| − | How can we overcome these difficulties? With (as the | + | *The points tend to collapse on each other or move away from each other. |
| − | might call it) | + | [Figure of this phenomenon] |
| + | How can we overcome these difficulties? With (as the Spanish developers | ||
| + | might call it) "De Le-vel set." (pronounced with the long e sound which doesn't really exist in English so much.) | ||
=The Level Set Approach= | =The Level Set Approach= | ||
| − | This method was developed by Osher and Sethian | + | This method was developed by Osher and Sethian [spelling?]. |
Assume we are evolving a curve in <math>\mathbb{R}^{2}</math>. Instead of doing | Assume we are evolving a curve in <math>\mathbb{R}^{2}</math>. Instead of doing | ||
| − | this, we evolve a surface in <math>\mathbb{R}^{3}</math> for which the | + | this, we evolve a surface in <math>\mathbb{R}^{3}</math> for which the ``zero |
level set,'' that is the intersection with the z=0 plane is the curve | level set,'' that is the intersection with the z=0 plane is the curve | ||
we wish to evolve. | we wish to evolve. | ||
| − | + | [Figure of an evolving curve] | |
| − | + | [Figure of evolving surface instead of curve] | |
Although evolving such a surface can be challenging, it is definitely | Although evolving such a surface can be challenging, it is definitely | ||
| Line 208: | Line 229: | ||
the zero-set (our curve) can change topologies and have singularities. | the zero-set (our curve) can change topologies and have singularities. | ||
| − | From the | + | From the [http://en.wikipedia.org/wiki/Dromedary Dromedary] (French: Dromadaire) to the [http://en.wikipedia.org/wiki/Bactrian_camel Camel] (French: Chameau) |
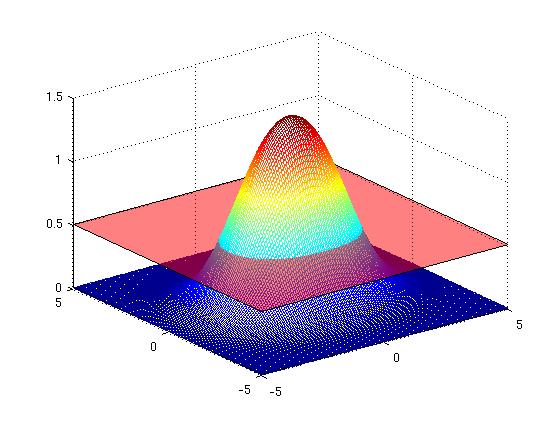
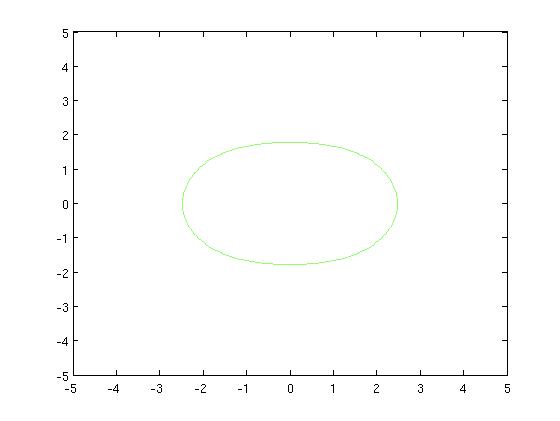
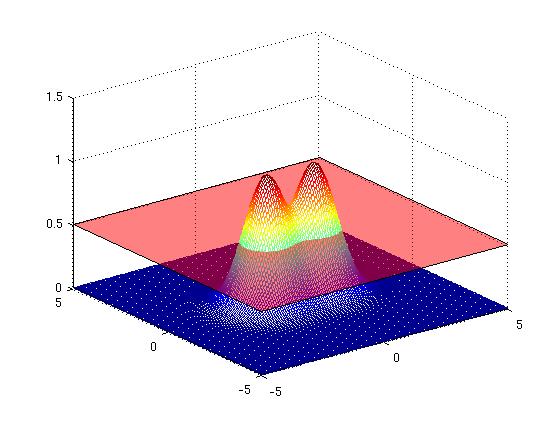
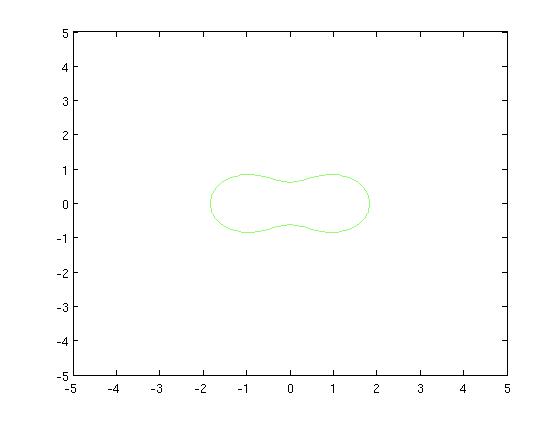
| − | + | [Figure t=0: of the one-hump animal, yielding a single curve] | |
| − | + | [[Image:camel1_Old Kiwi.jpg]] [[Image:camel1contour_Old Kiwi.jpg]] | |
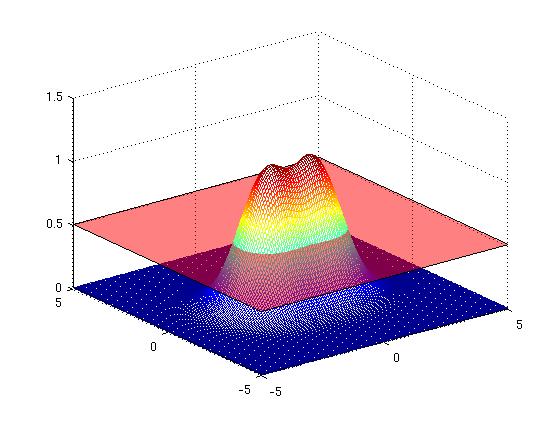
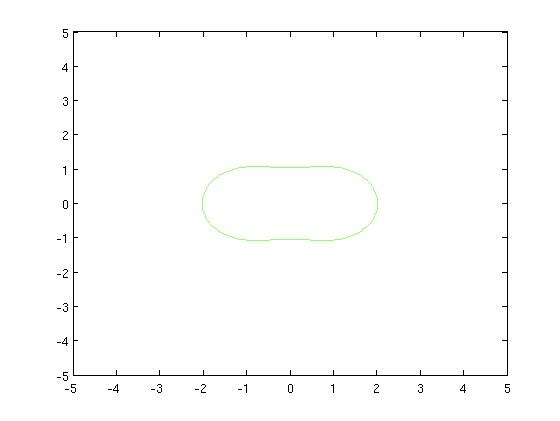
| − | + | [Figure t=1: The top flattens, the curve turns into a peanut] | |
| − | + | [[Image:camel2_Old Kiwi.jpg]] [[Image:camel2contour_Old Kiwi.jpg]] | |
| + | |||
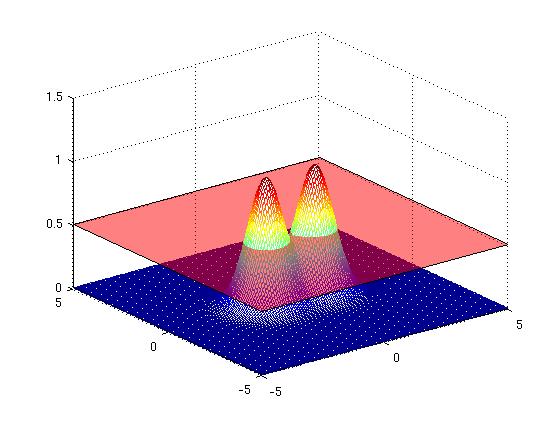
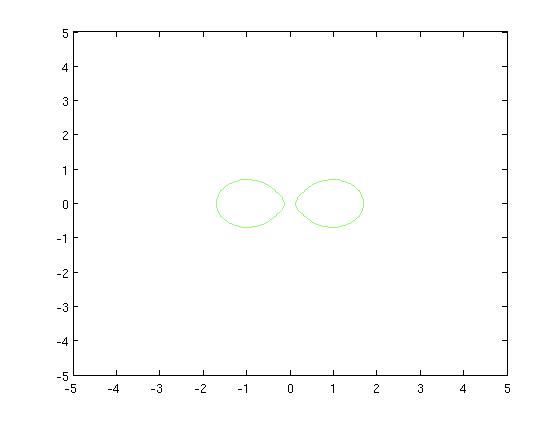
| + | [Figure t=2: The valley dips so we get the Chameau] | ||
| + | |||
| + | [[Image:camel3_Old Kiwi.jpg]] [[Image:camel3contour_Old Kiwi.jpg]] | ||
| + | |||
| + | [Figure t=3: The Chameau sinks deeper in the water so that only two humps appear. The curve splits into two] | ||
| + | |||
| + | [[Image:camel4_Old Kiwi.jpg]] [[Image:camel4contour_Old Kiwi.jpg]] | ||
We evolve the surface until it converges, and then we can look at | We evolve the surface until it converges, and then we can look at | ||
| Line 222: | Line 251: | ||
them a-priori. | them a-priori. | ||
| − | What PDE describes this surface evolution? | + | As a note for those who are not taking this class: We use French here because that is the mother language of our professor (Mimi), and because we were having difficulty finding the English words for these at first! (And by "we", we do mean the entire class.) |
| + | |||
| + | == What PDE describes this surface evolution? == | ||
Suppose <center><math> | Suppose <center><math> | ||
| Line 232: | Line 263: | ||
curve we are evolving. The Euler form of the level set is <center><math> | curve we are evolving. The Euler form of the level set is <center><math> | ||
\frac{d\phi}{dt}=f(t,\tau)||\nabla\phi||</math></center> | \frac{d\phi}{dt}=f(t,\tau)||\nabla\phi||</math></center> | ||
| − | |||
| − | |||
=Conclusion= | =Conclusion= | ||
And that's it for the semester! Have fun! | And that's it for the semester! Have fun! | ||
| + | ---- | ||
| + | Previous: [[Lecture_27_-_Clustering_by_finding_valleys_of_densities_Old_Kiwi|Lecture 27]] | ||
| + | |||
| + | [[ECE662:BoutinSpring08_OldKiwi|Back to ECE662 Spring 2008 Prof. Boutin]] | ||
| + | [[Category:ECE662]] | ||
| + | [[Category:decision theory]] | ||
| + | [[Category:lecture notes]] | ||
Latest revision as of 08:55, 17 January 2013
Contents
Lecture 28, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
The Last Class
Welcome to the last class of the semester! The kiwi is going to be a great resource.
Partial Differential Equations (Continued)
[Note: I do not think the difference between $ \partial $ and $ d $ is very important -- feel free to fix it if you disagree. I'm also a little sloppy with the vector symbols]
We may discretize this using a finite difference equation.
where $ u(t,x) $ is the initial guess. But we can also look at this
What does this mean? Let's consider an example.
This is the same as convolution:
[Figure: [1/3,1/3,1/3]*[(x-delx),*(x),(x+delx)]u(t,.) ]
At each successive time step, the convolution iterates on the results of the previous convolution until the solution stabilizes. (That is, until we reach the steady state solution, where $ \frac{du}{dt}=0\Longrightarrow u_{xx}=0 $)
We can use heat flow to smooth out parametric curves.
e.g. in $ \mathbb{R}^{2} $, consider the curve
We shall commonly drop the vector notation in the rest of this discussion.
[Figure: Arbitrary curve , looping from $ \tau=0 $ to $ \tau=10,000 $.]
And consider the family
satisfying the 2D heat equation
This gives us two 1-D heat equations
The solution to these equations is
If we cannot solve these analytically, we can again discretize the
solution.
Note that $ \Delta\tau\neq\Delta x $. $ \Delta\tau $ is the spacing
between the parameters, and is a constant. However, $ \Delta x $ is
the spacing of the points in the x direction, and it is certainly
not constant around the entire curve! And a little note on notation:
[Figure showing the notation]
At this point in the class, we reviewed how to solve differential equations iteratively.
How does this apply to valley-finding?
Use estimated density $ p(x) $ to define the energy of the curve in
the feature space. The simplest formulation is
It's funny that rivers solve PDEs. They find the minimal energy route
through the valleys. This is exactly what we want, because the valleys
separate the mountains, which are our clusters.
Look for a curve that minimizes E. For example, in 2D feature space, look for a curve in $ \mathrm{R}^{2} $, say $ c(\tau)=(x(\tau),y(\tau)) $,
such that
Numerically, we need to discritize the left hand side, but not the
[Figure of density points and approximated density landscape.]
[Start with curve around both mountains, this is the initial guess for the boundaries of the feature space]
[Note that the curve is discritized, each point is assigned to a different value of $ \tau $]
We can represent the points on the curve in a matrix
Then we can iterate using the equation above to find the boundaries
which minimizes the energy, and is thus the best seperation of the
clusters.
Issues with this approach
- We must fix the number of clusters
- We must assume the curve has some degree of smoothness.
[Figure of this phenomenon]
- The points tend to collapse on each other or move away from each other.
[Figure of this phenomenon] How can we overcome these difficulties? With (as the Spanish developers might call it) "De Le-vel set." (pronounced with the long e sound which doesn't really exist in English so much.)
The Level Set Approach
This method was developed by Osher and Sethian [spelling?].
Assume we are evolving a curve in $ \mathbb{R}^{2} $. Instead of doing this, we evolve a surface in $ \mathbb{R}^{3} $ for which the ``zero level set, that is the intersection with the z=0 plane is the curve we wish to evolve.
[Figure of an evolving curve]
[Figure of evolving surface instead of curve]
Although evolving such a surface can be challenging, it is definitely worth it, because our curve may undergo topology changes. How can this happen? Even though the surface evolves without topology changes, the zero-set (our curve) can change topologies and have singularities.
From the Dromedary (French: Dromadaire) to the Camel (French: Chameau)
[Figure t=0: of the one-hump animal, yielding a single curve]
[Figure t=1: The top flattens, the curve turns into a peanut]
[Figure t=2: The valley dips so we get the Chameau]
[Figure t=3: The Chameau sinks deeper in the water so that only two humps appear. The curve splits into two]
We evolve the surface until it converges, and then we can look at the resulting zero-set and count the clusters. We do not need ot know them a-priori.
As a note for those who are not taking this class: We use French here because that is the mother language of our professor (Mimi), and because we were having difficulty finding the English words for these at first! (And by "we", we do mean the entire class.)
What PDE describes this surface evolution?
Supposewhere $ \overrightarrow{N}(t,\tau) $ is normal to the curve. This is a very general equation because any curve evolution can be expressed in this fashion. Then we can consider a surface evolving$ \phi(x,y,t):=\mathbb{R}^{2}\times\mathbb{R}\rightarrow $a zero-level set at t, $ \left\{ x,y|\phi(x,y,t)=0\right\} $ is the
curve we are evolving. The Euler form of the level set isConclusion
And that's it for the semester! Have fun!
Previous: Lecture 27