| Line 1: | Line 1: | ||
| + | =Lecture 12, [[ECE662]]: Decision Theory= | ||
| + | |||
| + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. | ||
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| + | |||
| + | |||
__TOC__ | __TOC__ | ||
Latest revision as of 08:49, 17 January 2013
Lecture 12, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Contents
Support Vector Machines
(Continued from Lecture 11)
- Definition
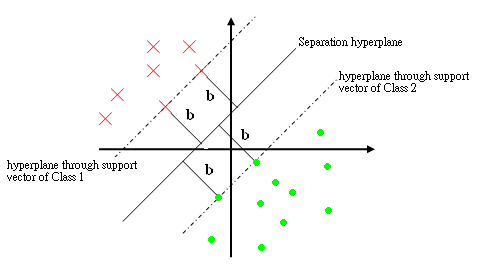
The support vectors are the training points $ y_i $ such that $ \vec{c}\cdot{y_i}=b,\forall{i} $. i.e. they are the closest to the hyperplane.
- How to Train a Support Vector Machine (SVM)
We want to find a $ \vec{c} $ such that $ \vec{c}\cdot{y_i} \geq b, \forall{i} $. This however, is wishful thinking, so we try to find this for as many training samples as possible with $ b $ as large as possible.
Observe: If $ \vec{c} $ is a solution with margin $ b $, then $ \alpha\vec{c} $ is a solution with margin $ \alpha b, \forall{\alpha} \in \Re > 0 $
So to pose the problem well, we demand that $ \vec{c}\cdot{y_i} \geq 1, '\forall{i}' $ and try to minimize $ \vec{c} $
- For small training sets, we can use a training method similar to online perceptron_Old Kiwi
- Pick a plane |c_vector|
- Find the worst classified sample. |yi_0| (Note: This step is computationally expensive for large data sets)
- Move plane |c_vector| to improve the classification
- Repeat steps 2-3 until the algorithm converges
We want to minimize $ ||\vec{c}|| $ subject to the constraints $ \vec{c}\cdot{y_i} = 1, \forall{i} $ (i.e. correct classification). Note: Optimizing $ ||\vec{c}|| $ is hard, because the function is not convex. Instead, optimize $ \frac{1}{2}||\vec{c}||^2 $ (convex function with the same optimum).
This gives a Quadratic Optimization Problem_Old Kiwi: Minimize $ \frac{1}{2}||\vec{c}||^2 $ subject to the constraints $ \vec{c}\cdot{y_i} = 1, \forall{i} $. However, we should demand that $ \vec{c}\cdot{y_i} = 1, \forall $ support vectors $ y_i $.
Formulate using Lagrange multipliers_Old Kiwi: (Someone should continue the notes from this point)
Karush-Kuhn-Tucker Construction
Reformulate as "Dual Problem"
Maximize $ L(\alpha)=\displaystyle \sum_{i} \alpha_{i}-\frac{1}{2}\sum_{i,j} \alpha _i \alpha_j y_i \cdot y_j $, where i, j are indices of SV.
Under constraint $ \displaystyle \sum_{i=1}^{d_1}\alpha _i - \sum_{i=d+1}^{d} \alpha _i = 0 $, and $ \alpha_i \geq 0, \quad \forall{i} $
Then find $ \vec{c}=\sum_{i} \alpha_{i} y_i $.
- Key points:
- L only depends on SV
- L only depends on $ y_{i} \cdot y_{j} $, not $ y_i $ or $ y_j $ explicitly.
Recall: maximize $ L(c,\vec{\alpha})=\frac{1}{2}||\vec{c}||^2 - \displaystyle \sum_{i} \alpha _i (\vec{c} \cdot y_i -1 ) $
When data is not linearly separable, max $ L(c,\vec{\alpha})=\infty $, Do not try this numerial optimization.
How to train a support vector machine using nonlinearly separable data:
Define "soft margins" by introducing "slack variable" $ \xi_i $ , which measure misclassification of $ y_i $. This means we introduce penalty terms through the modified conditions below:
$ \vec{c} \cdot y_i \geq 1 \Rightarrow \vec{c} \cdot y_i \geq 1 - \xi _i $ (try to use as few non-zero penalty terms as possible).
Quadratic Optimization Problem
Minimize $ \frac{1}{2}||\vec{c}||^2 + constant \displaystyle \sum_{i=1}^{d} \xi _i $
Subject to $ \vec{c} \cdot y_i \geq 1 - \xi _i, \quad \forall{i} $
- The Kernel Trick
Proposed by Aizerman in another context used by Vapnik,Boser, Guyon to upgrade SVM_Old Kiwi to find non-linear decision boundary based on observation that SVM_Old Kiwi training only introduces $ y_i\cdot{y_j} $.
$ y_i \cdot y_j = \varphi (x_i) \cdot \varphi (x_j) $
A kernel function $ K:\Re ^k \times \Re ^k \rightarrow \Re $ for a given mapping $ \varphi $ is a function such that $ K(x,x')=\varphi (x) \cdot \varphi (x') $.
Therefore, $ y_i \cdot y_j = K(x_i,x_j) $ $ \rightarrow $ No need to compute $ \varphi (x_i), \varphi (x_j) $ and no need to know $ \varphi $.
In order to exploit kernel trick, we need to have good kernel functions. One way to do that is to choose $ \varphi (x) $ (called basis functions) and use it to find corresponding kernel. Another method is to construct kernel functions directly by making sure that the function is a valid kernel which means it corresponds to a scalar product in some feature space.
The necessary and sufficient condition for a function to be a valid kernel is for the Gram Matrix K whose elements are $ k(x_n, x_m) $ to be positive semidefinite_Old Kiwi.
A powerful method for creating good kernel functions is to use simpler kernel functions to build new ones. We can manipulate kernel functions by using some transformations such as scalar multiplications, summing two kernel functions, inserting kernel functions into some other functions and so on.
Some nice examples using support vector machines can be found in Support Vector Machine Examples_Old Kiwi and SVM-2D_Old Kiwi.
- One example of kernel functions:
Take $ \varphi (x_1 , x_2)=(x_1^2,\sqrt{2} x_1 x_2, x_2^2 ) $
then, $ \varphi (x_1 , x_2) \varphi (\acute{x_1} , \acute{x_2})=x_1^2 \acute{x_1^2}+2x_1 x_2 \acute{x_1} \acute{x_2} + x_2^2 \acute{x_2^2} $
$ (x_1^2 \acute{x_1^2} + x_2^2 \acute{x_2^2} )^2 = [(x_1, x_2) (\acute{x_1^2}, \acute{x_2^2})]^2 $
Here kernel is $ K(\vec x, \acute{\vec x} ) = (\vec x, \acute{\vec x} )^2 $
Note : K is kernel for other functions $ \varphi $
For example, $ \varphi (x_1 , x_2) = \frac {1}{\sqrt{2}} (x_1^2 - x_2^2, 2x_1^2 x_2^2, x_1^2 + x_2^2) $
One-to-one correspondence between kernel and mapping $ \varphi $'s.