Link title

Introduction

Medical imaging systems cannot directly create a 3D scan of a person. They can only measure projections through an object with density. A Radon Transform is an integral that allows the calculation of the projections of an object as it is scanned. Since the scanner rotates as it takes data, the projections will have to be calculated at various angles. Thus coordinate rotation is an essential topic for tomographic reconstruction because it allows the calculation of the Radon Transform.

Coordinate Rotation

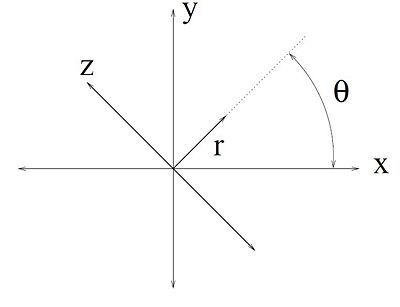
To accommodate the multitude of angles that scans will we taken at, we will introduce a new coordinate system to work with, $ (r,z) $. The relationship between $ (x,y) $ and $ (r,z) $ is shown below. The $ (r,z) $ axes are rotated counterclockwise by $ \theta $ relative to the $ (x,y) $ axes. The geometric meaning of $ (r,z) $ is shown in Figure 1.
$ \begin{bmatrix} x \\ y \end{bmatrix} = \mathbf{A_{\theta}}\begin{bmatrix} r \\ z \end{bmatrix} $

Where $ A_\theta $ is the counterclockwise rotation matrix

$ \mathbf{A_{\theta}}=\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} $

Fig 1: Geometric Interpretation of Rotated Coordinate System

The inverse transformation can be achieved by rotating the opposite direction. Essentially plug in $ -\theta $. This yields
$ \begin{bmatrix} r \\ z \end{bmatrix} = \mathbf{A_{-\theta}}\begin{bmatrix} x \\ y \end{bmatrix} $

Where $ A_{-\theta} $ is
$ \mathbf{A_{-\theta}} = \begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix} $

Radon Transform

The goal is to find an equation to express a projection $ p_\theta (r) $ of an object with density $ f(x,y) $. Let us consider an image with density $ f(x,y) $ shown in Figure 2.

[[Image:]]

Because we have defined the object in the $ (x,y) $ domain, we can only reference its actual values with $ x $ and $ y $. In order to work with the projection on $ z $, we must map $ (x,y) $ to $ (r,z) $ through the coordinate rotation covered above.

The projection integral for each $ \theta $ is given below.
$ \begin{align} p_{\theta}(r) &= \int_{-\infty}^{\infty}f( \begin{bmatrix} x \\ y \end{bmatrix}) dz \\ &= \int_{-\infty}^{\infty}f( \begin{bmatrix} r \\ z \end{bmatrix}) dz \\ &= \int_{-\infty}^{\infty} f( \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} r \\ z \end{bmatrix}) dz \\ &= \int_{-\infty}^{\infty} f(r\cos(\theta)-z\sin(\theta),r\sin(\theta)+z\cos(\theta))dz \end{align} $

References:
[1] C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.

Back to Honors Contract Main Page