| Line 38: | Line 38: | ||
---- | ---- | ||
| − | + | Motivation: Before introducing FST some background | |
| − | + | <math>A_{\theta}</math> is the counterclockwise rotation matrix given by <br/> | |
| − | + | <math>A_{\theta}=\begin{bmatrix} | |
| − | <math>\begin{bmatrix} | + | |
\cos(\theta) & -\sin(\theta) \\ | \cos(\theta) & -\sin(\theta) \\ | ||
\sin(\theta) & \cos(\theta) | \sin(\theta) & \cos(\theta) | ||
| − | \end{bmatrix}</math> | + | \end{bmatrix}</math><br/> |
| + | |||
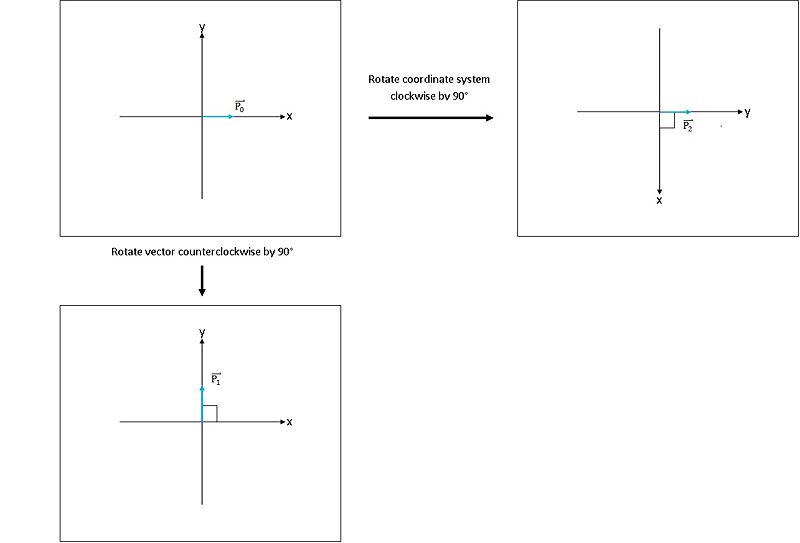
| + | The matrix rotates vector <math>v_0</math> in a 2-dimensional real space by angle <math>\theta</math> in a fixed coordinate system. Notice that this is equivalent to keeping the vector fixed and rotating the coordinate system ''clockwise'' by <math>\theta</math>. This equivalence is illustrated in figure 1. | ||
| + | |||
| + | |||
| + | [[Image:CR_fig1_mh.jpeg|800px|thumb|left|Fig 1: bottom left: ccw rotation of vector; top right: cw rotation of coordinate axes]] | ||
| + | |||
| + | Vector | ||
| − | + | Let us define a new coordinate system <math>(r,z)</math> where<br/> | |
<math>\begin{bmatrix} | <math>\begin{bmatrix} | ||
x \\ | x \\ | ||
| Line 57: | Line 63: | ||
</math> | </math> | ||
| + | i.e. vector <math>[r,z]'</math> is rotated counterclockwise angle <math>\theta</math> to produce vector <math>[x,y]'</math> | ||
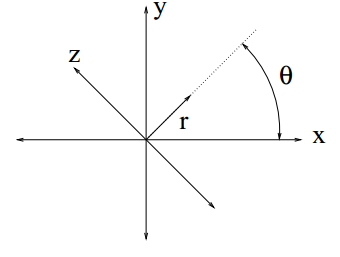
| + | Figure 1 shows the geometric interpretation of the rotation. | ||
| − | [[Image:CR_fig1.png| | + | [[Image:CR_fig1.png|600px|thumb|left|Fig 1: Geometric Interpretation]] |
Revision as of 05:48, 22 May 2013
The Bouman Lectures on Image Processing
A sLecture by Maliha Hossain
Subtopic 3: Co-ordinate Rotation
© 2013
Contents
Excerpt from Prof. Bouman's Lecture
Accompanying Lecture Notes
Motivation: Before introducing FST some background
$ A_{\theta} $ is the counterclockwise rotation matrix given by
$ A_{\theta}=\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} $
The matrix rotates vector $ v_0 $ in a 2-dimensional real space by angle $ \theta $ in a fixed coordinate system. Notice that this is equivalent to keeping the vector fixed and rotating the coordinate system clockwise by $ \theta $. This equivalence is illustrated in figure 1.
Vector
Let us define a new coordinate system $ (r,z) $ where
$ \begin{bmatrix} x \\ y \end{bmatrix} = A_{\theta}\begin{bmatrix} r \\ z \end{bmatrix} $
i.e. vector $ [r,z]' $ is rotated counterclockwise angle $ \theta $ to produce vector $ [x,y]' $
Figure 1 shows the geometric interpretation of the rotation.
- Inverse Transformation
$ \begin{bmatrix} r \\ z \end{bmatrix} = A_{-\theta}\begin{bmatrix} x \\ y \end{bmatrix} $
References
- C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.
- E. W. Weisstein, "Rotation Matrix." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RotationMatrix.html. May 8th, 2013 [May 21st, 2013]
Questions and comments
If you have any questions, comments, etc. please post them on this page
Back to the "Bouman Lectures on Image Processing" by Maliha Hossain