m (Protected "ECE600 F13 set theory review mhossain" [edit=sysop:move=sysop]) |
|||
| (24 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | [[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]]<br/> | ||
| + | [[ECE600_F13_probability_spaces_mhossain|Next Topic: Probability Spaces]] | ||
| + | ---- | ||
[[Category:ECE600]] | [[Category:ECE600]] | ||
| + | [[Category:probability]] | ||
[[Category:lecture notes]] | [[Category:lecture notes]] | ||
| + | [[Category:slecture]] | ||
<center><font size= 4> | <center><font size= 4> | ||
| − | '''Random Variables and Signals''' | + | [[ECE600_F13_notes_mhossain|'''The Comer Lectures on Random Variables and Signals''']] |
</font size> | </font size> | ||
| − | <font size= 3> | + | [https://www.projectrhea.org/learning/slectures.php Slectures] by [[user:Mhossain | Maliha Hossain]] |
| + | |||
| + | <font size= 3> Topic 1: Set Theory Review</font size> | ||
</center> | </center> | ||
| − | + | ---- | |
---- | ---- | ||
| Line 27: | Line 34: | ||
'''Definition''' <math>\qquad</math> Let <math>A</math> and <math>B</math> be two sets. Then, <br/> | '''Definition''' <math>\qquad</math> Let <math>A</math> and <math>B</math> be two sets. Then, <br/> | ||
<center><math>\begin{align} | <center><math>\begin{align} | ||
| − | A = B &\Longleftrightarrow \omega \in A \Rightarrow \omega \in B \;\and\; \omega \in B \Rightarrow \omega \in A \\ | + | A = B &\Longleftrightarrow \omega \in A \Rightarrow \omega \in B \;\mbox{and}\; \omega \in B \Rightarrow \omega \in A \\ |
| − | &\Longleftrightarrow A \subset B \;\and\; B \subset A | + | &\Longleftrightarrow A \subset B \;\mbox{and}\; B \subset A |
\end{align}</math></center> | \end{align}</math></center> | ||
| Line 36: | Line 43: | ||
<center><math>A\neq B</math></center> | <center><math>A\neq B</math></center> | ||
| − | '''Definition''' <math>\qquad</math> If <math>\omega</math>∈<math>A</math> ⇒ <math>\omega</math>∈<math>B</math>, then <math>A</math> is said to be a '''subset''' of <math>B</math>. if If <math>B</math> contains | + | '''Definition''' <math>\qquad</math> If <math>\omega</math>∈<math>A</math> ⇒ <math>\omega</math>∈<math>B</math>, then <math>A</math> is said to be a '''subset''' of <math>B</math>. if If <math>B</math> contains at least one element that is not in <math>A</math>, then <math>A</math> is a '''proper subset''' of <math>B</math>. We will simply call <math>A</math> a subset of <math>B</math> in either case, and write <math>A</math>⊂<math>B</math>. |
'''Definition''' <math>\qquad</math> the set with not elements is called the '''empty set''', or '''null set''' and is denoted Ø or {}. | '''Definition''' <math>\qquad</math> the set with not elements is called the '''empty set''', or '''null set''' and is denoted Ø or {}. | ||
| Line 55: | Line 62: | ||
'''Definition''' <math>\qquad</math> The '''intersection''' of sets <math>A</math> and <math></math> is defined as <br/> | '''Definition''' <math>\qquad</math> The '''intersection''' of sets <math>A</math> and <math></math> is defined as <br/> | ||
| − | <center><math>A\cap B \equiv \{\omega \in \mathcal{S}: \omega \in A \and \omega \in B\} </math> </center> | + | <center><math>A\cap B \equiv \{\omega \in \mathcal{S}: \omega \in A\; \mbox{and}\; \omega \in B\} </math> </center> |
<center>[[Image:fig2_set_theory.png|400px|thumb|left|Fig 2: A∩B is shown in green]]</center> | <center>[[Image:fig2_set_theory.png|400px|thumb|left|Fig 2: A∩B is shown in green]]</center> | ||
| Line 62: | Line 69: | ||
'''Definition''' <math>\qquad</math> The '''union''' of sets <math>A</math> and <math></math> is defined as <br/> | '''Definition''' <math>\qquad</math> The '''union''' of sets <math>A</math> and <math></math> is defined as <br/> | ||
| − | <center><math>A\cup B \equiv \{\omega \in \mathcal{S}: \omega \in A \or \omega \in B \; | + | <center><math>A\cup B \equiv \{\omega \in \mathcal{S}: \omega \in A \;\mbox{or}\; \omega \in B \; \mbox{or both}\} </math> </center> |
<center>[[Image:fig3_set_theory.png|400px|thumb|left|Fig 3: A∪B is shown in green]]</center> | <center>[[Image:fig3_set_theory.png|400px|thumb|left|Fig 3: A∪B is shown in green]]</center> | ||
| Line 76: | Line 83: | ||
'''Definition''' <math>\qquad</math> The '''set difference''' <math>A-B</math> or ''A\B'' is defined as <br/> | '''Definition''' <math>\qquad</math> The '''set difference''' <math>A-B</math> or ''A\B'' is defined as <br/> | ||
| − | <center><math>A-B \equiv \{\omega \in \mathcal{S}: \omega \in A\and \omega \notin B\} </math> </center> | + | <center><math>A-B \equiv \{\omega \in \mathcal{S}: \omega \in A\;\mbox{and}\; \omega \notin B\} </math> </center> |
Note that <br/> | Note that <br/> | ||
<center><math>A-B=A\cap B^c</math> </center> | <center><math>A-B=A\cap B^c</math> </center> | ||
| Line 93: | Line 100: | ||
==Algebra of Sets== | ==Algebra of Sets== | ||
| − | # Union is commutative ⇔ A ∪ B = B ∪ A | + | # Union is commutative ⇔ A ∪ B = B ∪ A ([[ECE600_F13_set_theory_review_proof1_mhossain|proof]]) |
| − | # Intersection is commutative ⇔ A ∩ B = B ∩ A | + | # Intersection is commutative ⇔ A ∩ B = B ∩ A ([[ECE600_F13_set_theory_review_proof2_mhossain|proof]]) |
| − | # Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C | + | # Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C ([[ECE600_F13_set_theory_review_proof3_mhossain|proof]]) |
| − | # Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C | + | # Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C (the proof is similar to the one for the associative property of the union) |
| − | # Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) | + | # Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) ([[ECE600_F13_set_theory_review_proof5_mhossain|proof]]) |
| − | # Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | + | # Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) ([[ECE600_F13_set_theory_review_proof56_mhossain|proof]]) |
| − | # (A')' = A | + | # (A')' = A ([[Complement_of_complement_mh|proof]]) |
| − | # | + | # De Morgan's Law: (A ∩ B)' = A' ∪ B' ([[De_Morgans_law_part_2|proof]]) |
| − | # | + | # De Morgan's Law: (A ∪ B)' = A' ∩ B' ([[De_Morgans_law_part_1|proof]]) |
| − | # ''S''' = Ø, where ''S'' is the sample space | + | # ''S''' = Ø, where ''S'' is the sample space (proof) |
| − | # A ∩ S = A | + | # A ∩ S = A ([[Intersection_with_universal_set_mh|proof]]) |
| − | # A ∩ Ø = Ø | + | # A ∩ Ø = Ø ([[Intersection_with_empty_set_mh|proof]]) |
| − | # A ∪ S = S | + | # A ∪ S = S ([[Union_with_universal_set_mh|proof]]) |
| − | # A ∪ Ø = A | + | # A ∪ Ø = A ([[Union_with_empty_set_mh|proof]]) |
| − | # A ∪ A' = S | + | # A ∪ A' = S (proof) |
| − | # A ∩ A' = Ø | + | # A ∩ A' = Ø (proof) |
| Line 122: | Line 129: | ||
* A set is '''uncountable''' if it is not finite or countable. A set that is uncountable cannot be written as <math>\{x_1,x_2,...\}</math>. Note that the set of reals as well as any interval in R is uncountable. | * A set is '''uncountable''' if it is not finite or countable. A set that is uncountable cannot be written as <math>\{x_1,x_2,...\}</math>. Note that the set of reals as well as any interval in R is uncountable. | ||
| + | |||
| + | Note that a finite or countable space (a collection of sets) may contain elements that are uncountable. For example the set {Ø,[0,1]} is a finite set with 2 elements but the interval [0,1] is uncountable. | ||
If you are interested to learn more about countable and uncountable sets, you may find this [[Math_Squad_infinity_review_of_set_theory_countablity_mhossain_S13|Math Squad tutorial]] useful. | If you are interested to learn more about countable and uncountable sets, you may find this [[Math_Squad_infinity_review_of_set_theory_countablity_mhossain_S13|Math Squad tutorial]] useful. | ||
| Line 132: | Line 141: | ||
* finite: <math>I=\{1,...,n\}</math> for some finite natural number n so that the collection of sets is <math>I=\{A_1,...,A_n\}</math> | * finite: <math>I=\{1,...,n\}</math> for some finite natural number n so that the collection of sets is <math>I=\{A_1,...,A_n\}</math> | ||
| − | * countable: <math>I</math> is the set of natural numbers i.e. <math>I=\{1,2,3,...\}</math>, so the collection is <math>\{ | + | * countable: <math>I</math> is the set of natural numbers i.e. <math>I=\{1,2,3,...\}</math>, so the collection is <math>\{A_1,A_2,A_3,...\}</math> |
| − | *uncountable: so the collection is <math>\{A_{\alpha}, \alpha</math>∈<math>I\}</math> | + | *uncountable: so the collection is <math>\{A_{\alpha}, \alpha</math>∈<math>I\}</math> for an uncountable set <math>I</math>. If <math>I=</math>'''R''', the set of reals, then the set in the collection can be written as <math>A_{\alpha}</math> for some real number <math> |
\alpha</math> | \alpha</math> | ||
'''Definition''' <math>\qquad</math> '''The union of an indexed family of sets''' is defined as <br/> | '''Definition''' <math>\qquad</math> '''The union of an indexed family of sets''' is defined as <br/> | ||
| − | <center><math>\bigcup_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; for | + | <center><math>\bigcup_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \;\mbox{for at least one} \; i\in I \}</math></center><br/> |
Note that if <math>I</math> is finite, we can write the union as <br/> | Note that if <math>I</math> is finite, we can write the union as <br/> | ||
<center><math>\bigcup_{i \in I}^n A_i</math></center> | <center><math>\bigcup_{i \in I}^n A_i</math></center> | ||
| Line 173: | Line 182: | ||
---- | ---- | ||
| + | |||
| + | ==[[Talk:ECE600_F13_set_theory_review_mhossain|Questions and comments]]== | ||
| + | |||
| + | If you have any questions, comments, etc. please post them on [[Talk:ECE600_F13_set_theory_review_mhossain|this page]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | [[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]]<br/> | ||
| + | [[ECE600_F13_probability_spaces_mhossain|Next Topic: Probability Spaces]] | ||
Latest revision as of 12:10, 21 May 2014
Back to all ECE 600 notes
Next Topic: Probability Spaces
The Comer Lectures on Random Variables and Signals
Topic 1: Set Theory Review
Contents
Definitions and Notation
Definition $ \qquad $ A set is a collection of objects called elements, numbers or points.
Notation $ \qquad $ $ \omega $∈$ A $ means $ \omega $ is an element of the set $ A $. $ \omega $∉$ A $ means $ \omega $ is not in the set $ A $.
There are two common ways to specify a set:
- Explicitly list all elements, e.g. $ \{1,2,3,4,5,6\} $
- Specify a rule for membership, e.g. $ A=\{\omega $∈$ Z:1 $ ≤ $ \omega $ ≤ $ 6\} $, i.e. the set of all integers between 1 and 6 inclusive. I prefer this notation for large or infinite sets.
Note that there is always a set that contains every possible element of interest. This set, along with some structure imposed upon the set, is called a space, denoted
Definition $ \qquad $ Let $ A $ and $ B $ be two sets. Then,
The proof that the second statement is equivalent is trivial and follows from the definition of the term subset, which is presented shortly.
If $ A $ and $ B $ are not equal, we write
Definition $ \qquad $ If $ \omega $∈$ A $ ⇒ $ \omega $∈$ B $, then $ A $ is said to be a subset of $ B $. if If $ B $ contains at least one element that is not in $ A $, then $ A $ is a proper subset of $ B $. We will simply call $ A $ a subset of $ B $ in either case, and write $ A $⊂$ B $.
Definition $ \qquad $ the set with not elements is called the empty set, or null set and is denoted Ø or {}.
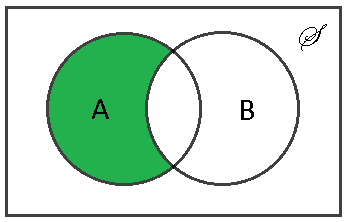
Venn Diagrams
A Venn diagram is a graphical representation of sets. It can be useful to gain insight into a problem, but cannot be used as a proof.
Set Operations
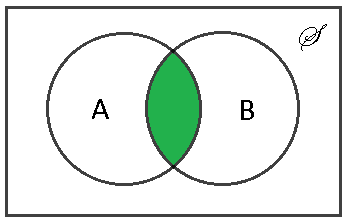
Definition $ \qquad $ The intersection of sets $ A $ and is defined as
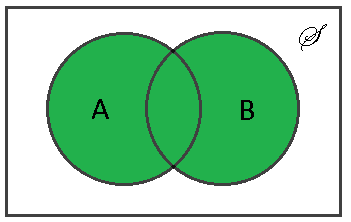
Definition $ \qquad $ The union of sets $ A $ and is defined as
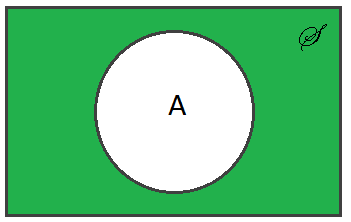
Definition $ \qquad $ The complement of a set $ A $, denoted $ A^c $, Ā, or A' is defined as
Definition $ \qquad $ The set difference $ A-B $ or A\B is defined as
Note that
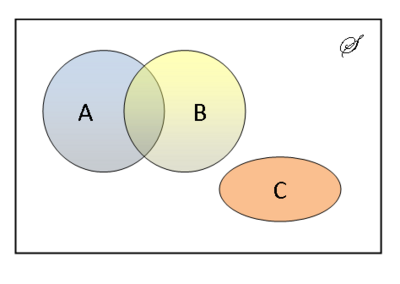
Definition $ \qquad $ Sets $ A $ and $ B $ are disjoint if $ A $ and $ B $ have not elements in common ie
In figure 1, A and C are disjoint. B and C are also disjoint.
Algebra of Sets
- Union is commutative ⇔ A ∪ B = B ∪ A (proof)
- Intersection is commutative ⇔ A ∩ B = B ∩ A (proof)
- Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C (proof)
- Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C (the proof is similar to the one for the associative property of the union)
- Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) (proof)
- Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (proof)
- (A')' = A (proof)
- De Morgan's Law: (A ∩ B)' = A' ∪ B' (proof)
- De Morgan's Law: (A ∪ B)' = A' ∩ B' (proof)
- S' = Ø, where S is the sample space (proof)
- A ∩ S = A (proof)
- A ∩ Ø = Ø (proof)
- A ∪ S = S (proof)
- A ∪ Ø = A (proof)
- A ∪ A' = S (proof)
- A ∩ A' = Ø (proof)
A Note on Sets of Different Sizes
We can categorize the sets we encounter three ways:
- A set $ A $ is finite if it contains an finite number of elements, i.e. the number of elements in the set is some natural number $ n $. Then we can list the elements in $ A $; e.g. $ A = \{x_1,...,x_n\} $.
- A set is countable if its elements can be put into a one-to-one correspondence (a bijection) with the integers. In this course when, we say countable, we mean countably infinite. We may write $ A=\{x_1,x_2,...\} $. The set of rationals is a countable set.
- A set is uncountable if it is not finite or countable. A set that is uncountable cannot be written as $ \{x_1,x_2,...\} $. Note that the set of reals as well as any interval in R is uncountable.
Note that a finite or countable space (a collection of sets) may contain elements that are uncountable. For example the set {Ø,[0,1]} is a finite set with 2 elements but the interval [0,1] is uncountable.
If you are interested to learn more about countable and uncountable sets, you may find this Math Squad tutorial useful.
We will often consider indexed collections of sets such as
where $ I $ is called the index set.
The index set can be
- finite: $ I=\{1,...,n\} $ for some finite natural number n so that the collection of sets is $ I=\{A_1,...,A_n\} $
- countable: $ I $ is the set of natural numbers i.e. $ I=\{1,2,3,...\} $, so the collection is $ \{A_1,A_2,A_3,...\} $
- uncountable: so the collection is $ \{A_{\alpha}, \alpha $∈$ I\} $ for an uncountable set $ I $. If $ I= $R, the set of reals, then the set in the collection can be written as $ A_{\alpha} $ for some real number $ \alpha $
Definition $ \qquad $ The union of an indexed family of sets is defined as
Note that if $ I $ is finite, we can write the union as
If $ I $ is countable, we can write the union as
If $ I $ is uncountable, we can write the union as
Definition $ \qquad $ The intersection of an indexed family of sets is defined as
Note that if $ I $ is finite, we can write the intersection as
If $ I $ is countable, we can write the intersection as
If $ I $ is uncountable, we can write the intersection as
Definition $ \qquad $ $ \{A_i, i $∈$ I\} $ is disjoint if $ A_i $∩$ A_j $ = Ø ∀ i,j∈I, i≠j.
Definition $ \qquad $ the collection $ \{A_i, i $∈$ I\} $ is a partition of S, the sample space, if it is disjoint and if
References
- M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.
Questions and comments
If you have any questions, comments, etc. please post them on this page