ECE600 F13 set theory review mhossain - Rhea

Topic 1: Set Theory Review

Definitions and Notation

Definition $\qquad$ A set is a collection of objects called elements, numbers or points.

Notation $\qquad$ $\omega$ ∈ $$ A $$ means $\omega$ is an element of the set $$ A $$ . $\omega$ ∉ $$ A $$ means $\omega$ is not in the set $$ A $$ .

There are two common ways to specify a set:

Explicitly list all elements, e.g. $\{1,2,3,4,5,6\}$
Specify a rule for membership, e.g. $A=\{\omega$ ∈ $$ Z:1 $$ ≤ $\omega$ ≤ $6\}$ , i.e. the set of all integers between 1 and 6 inclusive. I prefer this notation for large or infinite sets.

Note that there is always a set that contains every possible element of interest. This set, along with some structure imposed upon the set, is called a space, denoted

\mathcal{S}

\qquad

or

\qquad

\Omega .\

Definition $\qquad$ Let $$ A $$ and $$ B $$ be two sets. Then,

\begin{align} A = B &\Longleftrightarrow \omega \in A \Rightarrow \omega \in B \;\mbox{and}\; \omega \in B \Rightarrow \omega \in A \\ &\Longleftrightarrow A \subset B \;\mbox{and}\; B \subset A \end{align}

The proof that the second statement is equivalent is trivial and follows from the definition of the term subset, which is presented shortly.

If $$ A $$ and $$ B $$ are not equal, we write

A\neq B

Definition $\qquad$ If $\omega$ ∈ $$ A $$ ⇒ $\omega$ ∈ $$ B $$ , then $$ A $$ is said to be a subset of $$ B $$ . if If $$ B $$ contains at least one element that is not in $$ A $$ , then $$ A $$ is a proper subset of $$ B $$ . We will simply call $$ A $$ a subset of $$ B $$ in either case, and write $$ A $$ ⊂ $$ B $$ .

Definition $\qquad$ the set with not elements is called the empty set, or null set and is denoted Ø or {}.

Venn Diagrams

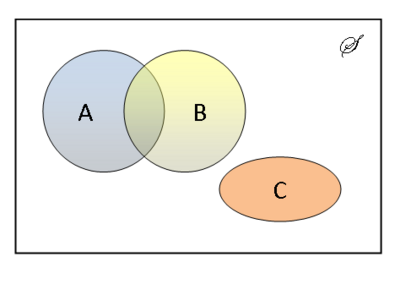
A Venn diagram is a graphical representation of sets. It can be useful to gain insight into a problem, but cannot be used as a proof.

Fig 1: An example of a Venn diagram

Set Operations

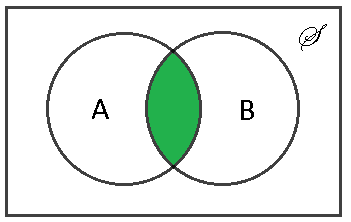
Definition $\qquad$ The intersection of sets $$ A $$ and is defined as

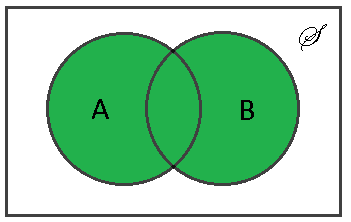
A\cap B \equiv \{\omega \in \mathcal{S}: \omega \in A\; \mbox{and}\; \omega \in B\}

Fig 2: A∩B is shown in green

Definition $\qquad$ The union of sets $$ A $$ and is defined as

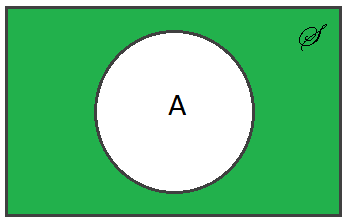
A\cup B \equiv \{\omega \in \mathcal{S}: \omega \in A \;\mbox{or}\; \omega \in B \; \mbox{or both}\}

Fig 3: A∪B is shown in green

Definition $\qquad$ The complement of a set $$ A $$ , denoted $$ A^c $$ , Ā, or A' is defined as

A^c \equiv \{\omega \in \mathcal{S}: \omega \notin A\}

Fig 4:

$ A^c $

is shown in green

Definition $\qquad$ The set difference $$ A-B $$ or A\B is defined as

A-B \equiv \{\omega \in \mathcal{S}: \omega \in A\;\mbox{and}\; \omega \notin B\}

Note that

A-B=A\cap B^c

Fig 5:

$ A-B $

is shown in green

Definition $\qquad$ Sets $$ A $$ and $$ B $$ are disjoint if $$ A $$ and $$ B $$ have not elements in common ie

A\cap B = \varnothing

In figure 1, A and C are disjoint. B and C are also disjoint.

Algebra of Sets

Union is commutative ⇔ A ∪ B = B ∪ A (proof)
Intersection is commutative ⇔ A ∩ B = B ∩ A (proof)
Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C (proof)
Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C (the proof is similar to the one for the associative property of the union)
Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) (proof)
Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (proof)
(A')' = A (proof)
De Morgan's Law: (A ∩ B)' = A' ∪ B' (proof)
De Morgan's Law: (A ∪ B)' = A' ∩ B' (proof)
S' = Ø, where S is the sample space (proof)
A ∩ S = A (proof)
A ∩ Ø = Ø (proof)
A ∪ S = S (proof)
A ∪ Ø = A (proof)
A ∪ A' = S (proof)
A ∩ A' = Ø (proof)

A Note on Sets of Different Sizes

We can categorize the sets we encounter three ways:

A set $$ A $$ is finite if it contains an finite number of elements, i.e. the number of elements in the set is some natural number $$ n $$ . Then we can list the elements in $$ A $$ ; e.g. $A = \{x_1,...,x_n\}$ .

A set is countable if its elements can be put into a one-to-one correspondence (a bijection) with the integers. In this course when, we say countable, we mean countably infinite. We may write $A=\{x_1,x_2,...\}$ . The set of rationals is a countable set.

A set is uncountable if it is not finite or countable. A set that is uncountable cannot be written as $\{x_1,x_2,...\}$ . Note that the set of reals as well as any interval in R is uncountable.

Note that a finite or countable space (a collection of sets) may contain elements that are uncountable. For example the set {Ø,[0,1]} is a finite set with 2 elements but the interval [0,1] is uncountable.

If you are interested to learn more about countable and uncountable sets, you may find this Math Squad tutorial useful.

We will often consider indexed collections of sets such as

\{A_i, i\in I\}

where $$ I $$ is called the index set.

The index set can be

finite: $I=\{1,...,n\}$ for some finite natural number n so that the collection of sets is $I=\{A_1,...,A_n\}$

countable: $$ I $$ is the set of natural numbers i.e. $I=\{1,2,3,...\}$ , so the collection is $\{A_1,A_2,A_3,...\}$

uncountable: so the collection is $\{A_{\alpha}, \alpha$ ∈ $I\}$ for an uncountable set $$ I $$ . If $$ I= $$ R, the set of reals, then the set in the collection can be written as $A_{\alpha}$ for some real number $\alpha$

Definition $\qquad$ The union of an indexed family of sets is defined as

\bigcup_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \;\mbox{for at least one} \; i\in I \}

Note that if $$ I $$ is finite, we can write the union as

\bigcup_{i \in I}^n A_i

If $$ I $$ is countable, we can write the union as

\bigcup_{i \in I}^{\infty} A_i

If $$ I $$ is uncountable, we can write the union as

\bigcup_{i \in I} A_i

as in the definition.

Definition $\qquad$ The intersection of an indexed family of sets is defined as

\bigcap_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; \forall \; i\in I \}

Note that if $$ I $$ is finite, we can write the intersection as

\bigcap_{i \in I}^n A_i

If $$ I $$ is countable, we can write the intersection as

\bigcap_{i \in I}^{\infty} A_i

If $$ I $$ is uncountable, we can write the intersection as

\bigcap_{i \in I} A_i

.

Definition $\qquad$ $\{A_i, i$ ∈ $I\}$ is disjoint if $$ A_i $$ ∩ $$ A_j $$ = Ø ∀ i,j∈I, i≠j.

Definition $\qquad$ the collection $\{A_i, i$ ∈ $I\}$ is a partition of S, the sample space, if it is disjoint and if

\bigcup_{i \in I} A_i = \mathcal{S}

References

M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes
Next Topic: Probability Spaces