Create the page "Power" on this wiki! See also the search results found.
- ==Signal Energy and Power==339 B (38 words) - 18:19, 5 September 2008
- == Power == ==Power Example==601 B (94 words) - 18:35, 5 September 2008
- on the other hand, power of a signal can be calculated by: Let's now calculate the energy and power of the following signal: <math>y(t) = x^{2}</math> for <math>t_1 = 0</math574 B (92 words) - 18:32, 5 September 2008
- on the other hand, power of a signal can be calculated by: Let's now calculate the energy and power of the following signal: <math>y(t) = x^{2}</math> for <math>t_1 = 0</math574 B (92 words) - 18:37, 5 September 2008
- Compute the energy and power of a CT signal <math>y=2e^t</math> from (0,10) ===Power===596 B (90 words) - 18:57, 5 September 2008
- == Power ==480 B (73 words) - 10:41, 7 September 2008
- y1 = power(t1, 3); y2 = power(t2-2, 3);1 KB (217 words) - 08:58, 12 September 2008
- ===Signal power and energy ===2 KB (243 words) - 08:04, 21 November 2008
- 4. x[n] has minimum power among all signals that satisfy 1,2,3. from 4, power of x[n] = <math>\frac {1}{6} \sum_{n=0}^{5} |x[n]|^2 = \sum_{n=0}^{5} |{a_k672 B (117 words) - 13:08, 25 September 2008
- 4. <math>x[n]\,</math> has a minimum power among all signals that satisfy rules 1-31 KB (203 words) - 16:00, 25 September 2008
- x[n] has min power among all signals that satisfy the above. Since the power is minimum all the other ak values are zero.938 B (182 words) - 07:09, 26 September 2008
- 4)x[n] has minimum power among all signals that satisfy the above properties. To minimize the power take <math>a_1=a_2=a_3=a_4=a_5=a_7=a_8=a_9=a_{10}=a_{11}=0</math>2 KB (426 words) - 15:21, 26 September 2008
- 4. x[n] has minimum power among all signals that satisfy 1,2,3. We want to minimize the power, so:719 B (121 words) - 16:44, 26 September 2008
- ...ot of 2 the signal provides the signal power of 1 unit when input into the power equation of specification (4).992 B (159 words) - 18:33, 26 September 2008
- 4.x[n] has minimum power among all the signals that satisfy 1,2,3. Power of x[n] is994 B (178 words) - 18:44, 26 September 2008
- 4. x[n] has minimum power among all the signals that satisfy 1,2,3 4. <math> \Rightarrow </math> To minimum the power, we set the rest of <math>a_k</math> to zero <br><br>1 KB (186 words) - 20:38, 26 September 2008
- ...how how to compute the Fourier transforms of CT and DT signals that have a power of absolute value (e.g. <math>(\frac{1}{2})^{|n|}</math>). First, I will sh1 KB (242 words) - 14:45, 24 October 2008
- ...es due to several advantages. An FM transmitter can always operate at peak power and any disruptions to or fading of the signal can be corrected at the rece1 KB (195 words) - 18:21, 17 November 2008
- ...range of z for which the z-transform converges. Since the z-transform is a power series, it converges when x[n]z−n is absolutely summable. Stated differen3 KB (537 words) - 17:27, 3 December 2008
- My favorite theorem is Cantor's theorem, which states that the power set of some set S has greater cardinality that that of S itself, whether S332 B (60 words) - 18:42, 2 September 2008
- ...ally makes sense to me as well. It is kind of playing with the order which power comes, that's the idea I get. ...take the inverse of both sides. And, can we bring the inverse in from the power? I am pretty sure it is ok to have the inverse of g^k is equal to the inver1 KB (264 words) - 17:12, 22 October 2010
- To find an order of an element, y in X, we just have to find a power of the modulo where it will repeat itself. So2 KB (339 words) - 17:04, 22 October 2010
- ...know if this found with a supercomputer or by distributing the processing power over a lot of PCs (like folding @ home)?3 KB (425 words) - 16:04, 12 October 2008
- 32 is the smallest non-trivial 5th power. 167 is the smallest number whose 4th power begins with 4 identical digits13 KB (2,062 words) - 13:16, 29 November 2010
- Monic means the leading coefficient is 1. Degree two means the highest power is 2. And irreducible means it doesn't factor interestingly. So each polyno1 KB (206 words) - 05:57, 13 November 2008
- ...ting of near and far points. Tuning this parameter controls the predictive power of the system. We have empirically optimized the value.13 KB (2,073 words) - 08:39, 17 January 2013
- * [[ES-3: Power Electronics and Electric Drives_Old Kiwi]]166 B (22 words) - 20:10, 9 March 2008
- | ? || ES-3 || ? || Power Electronics and Electric Drives2 KB (279 words) - 23:00, 9 March 2008
- * `Power Point slides on R programming <http://www.math.ntu.edu.tw/~hchen/Prediction2 KB (241 words) - 23:32, 11 March 2008
- ...the number of clusters he wants to split his data set into. It has to be a power of 2.903 B (157 words) - 01:07, 7 April 2008
- Capital Letters whose denominator is the highest power of its kind can be found directly as follows:4 KB (606 words) - 22:25, 1 May 2008
- ...<math>\Omega=[0,1]\frac{}{}</math>, the <math>\sigma-</math>algebra is the power set and counting measure.880 B (148 words) - 11:03, 22 July 2008
- Average Power:417 B (73 words) - 07:39, 16 June 2009
- Compute the energy and the average power of the following signal: ...energy is correct, but the derivation is wrong. The answer for the average power is wrong. Try not to skip so many steps, it will help you to make fewer mis6 KB (975 words) - 15:35, 25 February 2015
- [[Finite total energy means zero average power]]152 B (22 words) - 06:42, 19 June 2009
- [[Finite total energy means zero average power|If <math>E_\infty</math> is ''finite'', then <math>P_\infty</math> is ''zer561 B (96 words) - 07:39, 22 June 2009
- =Example of computation of Signal energy and Signal Power =2 KB (276 words) - 10:09, 16 September 2013
- Calculate the energy <math>E_\infty</math> and the average power <math>P_\infty</math> for the CT signal2 KB (408 words) - 17:20, 25 February 2015
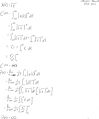
File:Sabrell HW1.jpg Energy Infinity and Power Infinity Calculations(2,428 × 2,930 (426 KB)) - 17:37, 21 June 2009- Calculate the energy <math>E_\infty</math> and the average power <math>P_\infty</math> for the CT signal ...ect, but you distributed the limit too early when you computed the average power, so your answer came out wrong. </span>1 KB (241 words) - 17:06, 25 February 2015
- Calculate the energy <math>E_\infty</math> and the average power <math>P_\infty</math> for the CT signal <span style="color:red"> The energy computation looks good. But in the power computation you distributed the limit too early and so your final answer is2 KB (415 words) - 17:05, 25 February 2015
- Calculate the energy <math>E_\infty</math> and the average power <math>P_\infty</math> for the CT signal3 KB (432 words) - 17:55, 25 February 2015
- * Signal properties (even/odd, periodicity, power, energy, etc.)5 KB (643 words) - 11:55, 6 August 2009
- ...only be used in case of an emergency and if for some reason (e.g, ECE-wide power outage) we are unable to use Rhea. Note also that this information will be1 KB (179 words) - 15:26, 27 August 2009
- ...ems with the server running Rhea (for example in the case of a campus-wide power outage), we will revert to email for communication. As Purdue's email acces2 KB (371 words) - 09:17, 10 August 2009
- ...only be used in case of an emergency and if for some reason (e.g, ECE-wide power outage) we are unable to use Rhea. Note also that this information will be826 B (132 words) - 09:01, 25 August 2009
- ...ems with the server running Rhea (for example in the case of a campus-wide power outage), we will revert to email for communication. As Purdue's email acces2 KB (370 words) - 09:01, 25 August 2009
- ...a_i ( X(z) z ^ {n-1})} \ </math> Coefficient of degree (-1) term on the power series expansion of <math> ( X(z) z ^ {n-1}) \ </math> <math> about a_i \ So inverting X(z) involves power series.2 KB (399 words) - 08:27, 23 September 2009
- 1.) Write X(z) as a power series2 KB (270 words) - 08:35, 23 September 2009
- ...oles a_i of X(z) z^{n-1}} \ </math> Coefficient of degree(-1) term in the power expansion of <math>X(z) z^{n-1} \ </math> about <math>a_i</math> So inverting X(z) involves power series2 KB (350 words) - 09:50, 23 September 2009

