(→Non-Periodic Signal) |
|||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:ECE301]] | ||
| + | [[Category:periodicity]] | ||
| + | =Periodic versus non-periodic functions ([[Homework_1_ECE301Fall2008mboutin|hw1]], [[ECE301]])= | ||
| + | <span style="color:green"> Read the instructor's comments [[hw1periodicECE301f08profcomments|here]]. </span> | ||
| + | |||
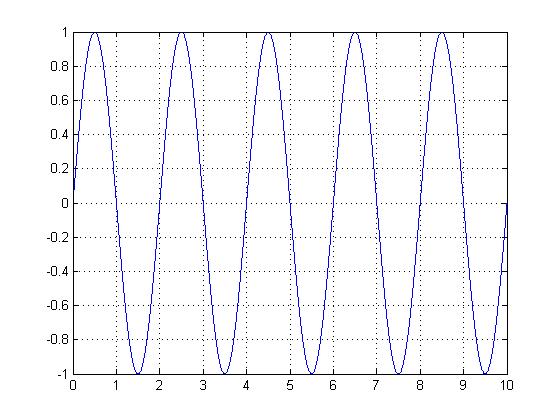
==Periodic Signal== | ==Periodic Signal== | ||
[[Image:periodic signal_ECE301Fall2008mboutin.jpg]] | [[Image:periodic signal_ECE301Fall2008mboutin.jpg]] | ||
| Line 4: | Line 9: | ||
Above is an example of a periodic signal: <math>y(t) = \sin(\pi t)</math> | Above is an example of a periodic signal: <math>y(t) = \sin(\pi t)</math> | ||
| − | The function is periodic because as can be seen from the graph <math>y(t+T)=y(t)</math> where T=2 seconds. | + | The function is periodic because as can be seen from the graph <math>y(t+T)= y(t)</math> where T=2 seconds. |
| − | + | ||
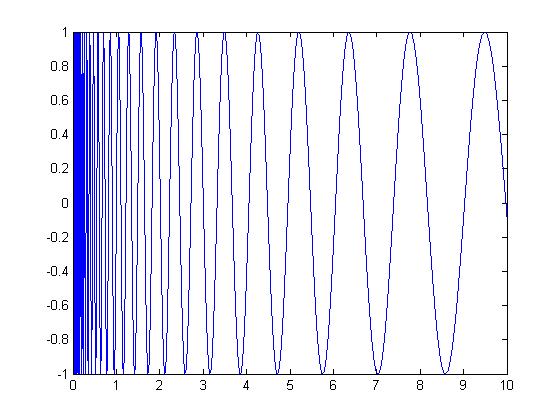
==Non-Periodic Signal== | ==Non-Periodic Signal== | ||
| Line 11: | Line 15: | ||
Represented above is an example of a non-periodic function: <math> y(t)=sin(10 \pi \ln(t))</math>. | Represented above is an example of a non-periodic function: <math> y(t)=sin(10 \pi \ln(t))</math>. | ||
| − | This function is clearly not periodic because the frequency changes with time and therefore <math>y(t+T)\ | + | This function is clearly not periodic because the frequency changes with time and therefore <math>y(t+T)\ne y(t)</math>. |
Latest revision as of 07:28, 14 April 2010
Periodic versus non-periodic functions (hw1, ECE301)
Read the instructor's comments here.
Periodic Signal
Above is an example of a periodic signal: $ y(t) = \sin(\pi t) $
The function is periodic because as can be seen from the graph $ y(t+T)= y(t) $ where T=2 seconds.
Non-Periodic Signal
Represented above is an example of a non-periodic function: $ y(t)=sin(10 \pi \ln(t)) $. This function is clearly not periodic because the frequency changes with time and therefore $ y(t+T)\ne y(t) $.