Instructor's Comments on periodic versus non-periodic functions (homework 1, ECE301)
I wanted to take this opportunity to comment on your answers to the hw1 question "Give an example of a periodic function, and an example of a non-periodic function.". By and large, your answers reflect the common conception of an undergraduate student at the beginning of the ECE301 course, namely that periodic functions are things like sine and cosine that oscillate all the time, and non-periodic functions are things like the exponential function, which grows all the time. However, in this course, I would like to begin thinking of periodic/non-periodic functions differently.
Fact 1: One can build a periodic function by adding shifted copies of another function
First, I would like you see that one can build a periodic function starting from any function. More precisely, one can take any function $ f(t) $ and shift it by $ T $, then by $ 2T $, $ 3T $, $ 4T $, etc. One can also shift it by $ -T $, $ -2T $, $ -3T $, etc. In other words, one can consider the shifted function $ f(t+kT) $, for any integer $ k\in Z $. By adding all these shifted functions together, one obtain a periodic function.
Claim: For any real number $N$, the function
$ x(t)=\sum_{k=-\infty}^{\infty} f(t+kN) $
is periodic with period $|N|$.
Proof Before proving this fact, it is useful to illustrate with a specific function. In order to be able to see what is going on, we choose a function with a compact support. For example, consider the function
$ f(t) = \left\{ \begin{array}{ll} \frac{sin(t)}{t}, & \text{ for } 0\leq t < 4\\ 0, & \text{ else.} \end{array} \right. $
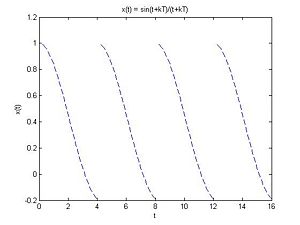
As one can see from its graph, this function is not periodic. However, the function
$ x(t)=\sum_{k=-\infty}^{\infty}f(t+4k) $
is periodic with period 4, because it is the repetition of the $ \frac{sin(t)}{t} $ part of $ f(t) $ an infinite number of times.
Below is the graph of $ x(t) $, for $ 0<t<16 $.
Now in order to prove that $ x(t) $ is periodic with period 4, we need to show that $ x(t+4)=x(t) $ for all $t$. We have
$ \begin{align} x(t+4) &= \left. \sum_{k=-\infty}^{\infty}f(t+4k)\right|_{t\rightarrow t+4},\\ &= \sum_{k=-\infty}^{\infty}f(t+4+4k),\\ &= \sum_{k=-\infty}^{\infty}f(t+4(1+k)),\\ &= \sum_{k'=-\infty}^{\infty}f(t+4k'),\text{ letting }k'=k+1, \\ &= x(t), \text{ since }k'\text{ is a dummy index}, \end{align} $
which completes the proof. As an exercise, you can try to prove that the function $ f(t)=\sum_{k=-\infty}^{\infty} \frac{1}{(x+1+3k)} $ is periodic. It is recommended that you get comfortable with such exercises before the exam.
Fact 2: One can obtain a non-periodic function by sampling a periodic function
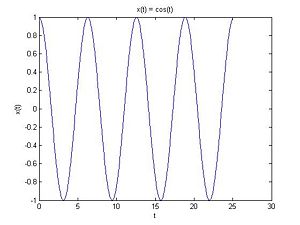
As everybody in the class seems to know quite well, the continuous-time signal $ x(t) = cos(t) $ is a periodic function with period $ 2\pi $. Here is the graph of $ x(t) $.
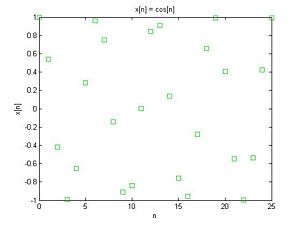
By sampling $ x(t) $ every $ T $, we obtain a discrete-time signal $ f[n] $. However, $ f[n] $ is not necessarily periodic: it depends what $ T $ is. For example, if $ T=1 $, then $ f[n] $ looks like this:
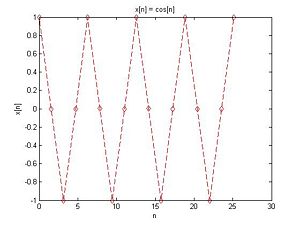
Interestingly, this discrete-time function is not periodic. However, if $ T=\pi/2 $, then $ f[n] $ $ is $ periodic, as one can see below.
So, when is a sampling of a periodic function periodic, and when is it not periodic? This is one thing we will study in class. Don't miss the lecture!