KNN Algorithm OldKiwi - Rhea

A summary of KNN and other non-parametric classification techniques (including pseudo-code)

ECE662: Statistical decision theory and decision making processes

(Supplement to the lecture notes)

Non-parametric techniques

The non-parametric density estimation is P(x) = k/(NV)

where,

k is the number of samples in V
N is the total number of samples
V is the volume surrounding x

This estimate is computed by two approaches

Parzen window approach

Fixing the volume V and determining the number k of data points inside V

KNN(K-Nearest Neighbor)

Fixing the value of k and determining the minimum volume V that encompasses k points in the dataset

The advantages of non-parametric techniques

No assumption about the distribution required ahead of time
With enough samples we can converge to an target density

The disadvantages of non-parametric techniques

If we have a good classification, the number of required samples may be very large
Computationally expensive

k-Nearest Neighbor (kNN) Algorithm

This algorithm is based on the observation that a sample that has features that are similar to the ones of points of one particular class it belongs to that class. These points are known as nearest neighbors. The parameter k specifies the number of neighbors (neighboring points) used to classify one particular sample point. Finally, the assignment of a sample to a particular class is done by having the k neighbors considered to "vote". In this fashion, the class represented by the largest number of points among the neighbors ought to be the class that the sample belongs to. The so called Nearest Neighbor algorithm is the particular instance of the kNN when k=1.

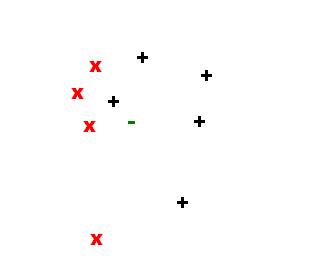
Consider the set of points in the feature space in the figure below:

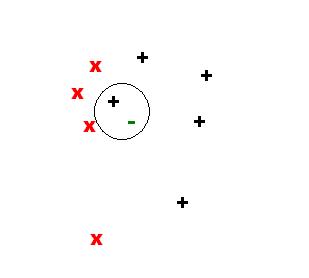
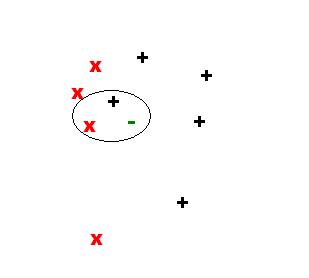
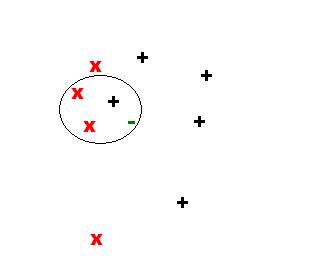
The next 3 figures illustrate the sample point in the feature space and neighbors for k={1,2,3}:

For k=1, we have:

For k=2, we have:

For k=3, we have:

Some of the important properties of the kNN algorithm are listed below:

The kNN can be used to classify data without requiring model building, this is called "instance-based learning".

A measurement of the distance between data points should be available

The kNN classification is based solely on local information (only the k nearest neighboring data points are inspected during the classification process).

The decision boundaries produced by the kNN classification can of of arbitrary shape

The classification is sensitive to the correct selection of k. If k is too small it will lead to "over-fitting"

The Algorithm's pseudo-code

Consider k as the desired number of nearest neighbors and $S:={p_1, ... , p_n}$ be the set of training samples in the form $$ p_1 = (x_i, c_i) $$ , where $$ x_i $$ is the d-dimensional feature vector of the point $$ p_i $$ and $$ c_i $$ is the class that $$ p_i $$ belongs to.

For each p'=(x',c')

Compute the distance $$ d(x', x_i) $$ between $$ p' $$ and all $$ p_i $$ belonging to S
Sort all points $$ p_i $$ according to the key $$ d(x',x_i) $$
Select the first $$ k $$ points from the sorted list, those are the $$ k $$ closest training samples to $$ p' $$
Assign a class to $$ p' $$ based on majority vote: $c' = argmax_y \sum_{(x_i,c_i)}$ belonging to S, $$ I(y=c_i) $$

end

Code available

"Instance-Based learning Java Implementation" [1]

References

"Introduction to Data Mining", P. Tan, M. Steinbach and V. Kumar, Addison-Wesley, 2006.

"Efficient Implementation of Nearest Neighbor Classification" [2]

"Efficient Implementation of Nearest Neighbor Classification" (Slides) [3]

"k-Nearest Neighbors" (Wikipedia) <http://en.wikipedia.org/wiki/Nearest_neighbor_(pattern_recognition)>

For more on KNN and other parametric density estimation techniques

See the lecture notes, especially:

Back to the lecture notes