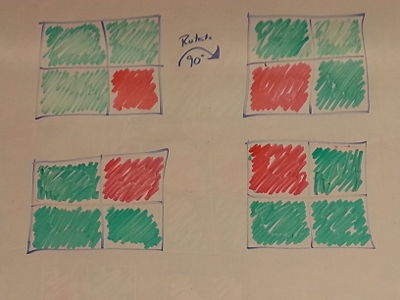
We discuss in class colorings of graphs, where adjacent vertices have different colors. Suppose you took the graph to be a polygon and allowed the graph to be reflected and rotated. How many different colorings do you get?
Contents
Outline/Title?
Introduction
In graph theory, it is sometimes necessary to find the number of ways to color the vertices of a polygon. Two theorems that work together to solve this problem are the Polya theorem and Burnside theorem.
Example 1: Square
A basic example of how to use the theorems is a simple two-coloring of a square.
Step 1: The six unique graphs are shown for a two-coloring of a 2x2 square:
Step 2: Finding the isomorphic graphs for each unique graph:
This provides a lists of all the different colorings possible.
| gggg | gggr | ggrg | rggg |
| grgg | ggrr | rgrg | rrgg |
| grrg | rgrr | grrr | rrgr |
| rrrg | rrrr | grrg | rggr |
Step 4: Applying the eight possible orbits to the various colorings:
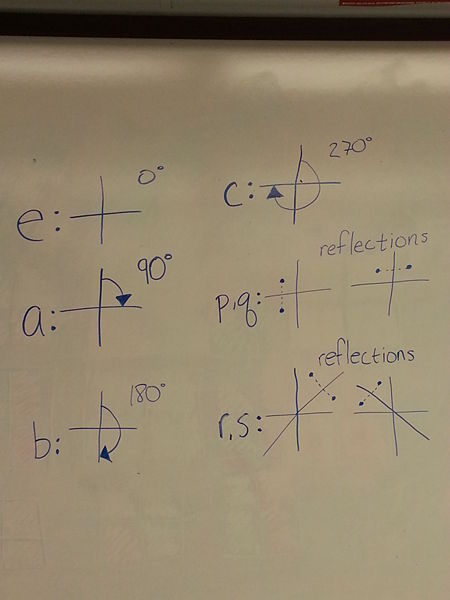
Orbit: An orbit is a term to describe the group of actions that act upon a set elements. In this example the actions are the basic motions of rotating and reflecting along a set axis and the motion that it induces on the points.
Below are examples used for a square.
This gives the following chart:
| e | a | b | c | p | q | r | s | |
| rrrr | rrrr | rrrr | rrrr | rrrr | rrrr | rrrr | rrrr | rrrr |
| grrr | grrr | rgrr | rrgr | rrrg | rgrr | rrrg | grrr | rrgr |
| rgrr | rgrr | rrgr | rrrg | grrr | grrr | rrgr | rrrg | rgrr |
| rrgr | rrgr | rrrg | grrr | rgrr | rrrg | rgrr | rrgr | grrr |
| rrrg | rrrg | grrr | rgrr | rrgr | rrgr | grrr | rgrr | rrrg |
| ggrr | ggrr | rggr | rrgg | grrg | ggrr | rrgg | grrg | rggr |
| rggr | rggr | rrgg | grrg | ggrr | grrg | rggr | rrgg | ggrr |
| rrgg | rrgg | grrg | ggrr | rggr | rrgg | ggrr | rggr | grrg |
| grrg | grrg | ggrr | rggr | rrgg | rggr | grrg | ggrr | rrgg |
| rgrg | rgrg | grgr | rgrg | grgr | grgr | grgr | rgrg | rgrg |
| grgr | rgrg | grgr | rgrg | grgr | grgr | grgr | rgrg | rgrg |
| gggr | gggr | rggg | grgg | ggrg | ggrg | rggg | grgg | gggr |
| ggrg | ggrg | gggr | rggg | grgg | gggr | grgg | ggrg | rggg |
| grgg | grgg | ggrg | gggr | rggg | grgg | ggrg | gggr | grgg |
| rggg | rggg | grgg | ggrg | ggr | grgg | gggr | rggg | ggrg |
| gggg | gggg | gggg | gggg | gggg | gggg | gggg | gggg | gggg |
| x | Ox | Sx |
| rrrr | {gggg} | G |
| grrr | {grrr,rgrr,rrgr,rrrg} | {e,r} |
| rgrr | {e,s} | |
| rrgr | {e,r} | |
| rrrg | {e,s} | |
| ggrr | {e,p} | |
| rggr | {e,q} | |
| rrgg | {e,p} | |
| grrg | {e,q} | |
| rgrg | {e,b,r,s} | |
| grgr | {e,b,r,s} | |
| gggr | {e,s} | |
| ggrg | {e,r} | |
| grgg | {e,s} | |
| rggg | {e,r} | |
| gggg | {gggg} | G |
Definitions:
- Burnside-The lemma counts the number of orbits of a set X acted upon by a group G. # of Orbits = (1/|G|) Sum over G |x^g|. Where x^g is an element of x such that g(x) = x, and |x^G| is the number of elements that fit this defintion.
- Polya-Applies this to colors.
'
'Formula:
- show formula
- breakdown of each element
- relate back to example 1
Proof:
References and Additional Information
For further reading on the Polya theorem:
http://arxiv.org/pdf/1001.0072.pdf
http://math.berkeley.edu/~mbaker/Tucker.pdf
http://www.whitman.edu/mathematics/SeniorProjectArchive/2012/Huisinga.pdf