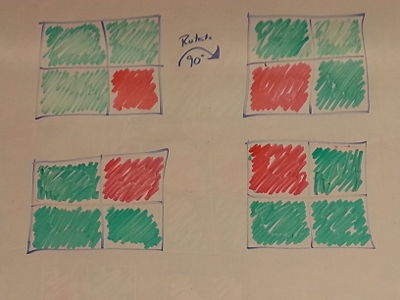
We discuss in class colorings of graphs, where adjacent vertices have different colors. Suppose you took the graph to be a polygon and allowed the graph to be reflected and rotated. How many different colorings do you get?
Theorems of Burnside and Polya
Introduction
In graph theory, it is sometimes necessary to find the number of ways to color the vertices of a polygon. Two theorems that work together to solve this problem are the Polya theorem and Burnside theorem. Below we will give specific examples on how to use these equations. We found that using this method is much easier and understandable than trying to understand the Theorems equations given with them.
Burnside
To begin, we will start with a simple 2 colored 2x2 square and eventually we will explain how to apply it for an n-colored 2x2 and a cube. From there the reader should have a basic understanding so that they could apply on n-colored n-gons.
We will first do it in a less mathematically rigourous method and then compare it to our later results. This also helps build intuition.
In order to find the total possible ways to color a 2x2 square with 2 colors, we take the number of colors and multiply it by itself for the total number of points. Giving the formula xn where x is the number of colors and n is the number of points. For this example we will use x=2 and n=2x2=4. Thus 24 =16 colorings. We show this in the picture below:
This is simple for a 2-coloring of an 2x2 square but to have a more scientific approach and to verify that our answer is correct then we have to use Burnside's Theorem.
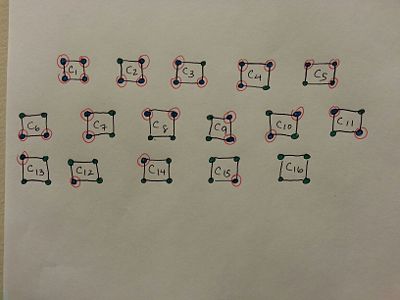
We will be using a different method of coloring, this time treating the square as a graph of connected verticies. We will also label each graph for use in the table belows.
The best way to show this is with a fairly complicated table:
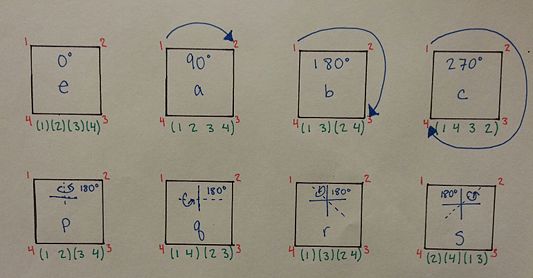
First we need to understand the notation shown in column 2. The picture below shows what each letter means:
These reflections and rotation are the the elements of the group G, we will call these the orbits. What is important is the number of orbits that are within G but we wil get to that in a little while. Now the next step is to take each of the orbits and apply them to the 16 original colorings and see which of the colorings are fixed, meaning that none of the verticies change color. Doing this will give you column 3. The number values is just the number of coloring that do not move for each line. Now let's take a look at the chart:
At this point we will look at the last column. The values of xpn are going to be used for the final equation of burnside and eventually for Polya. The value for p is the length it takes to get around the longest cycle while n is the number of individual cycles ( the green numbers).
For example if we take (1234) as cycle for the square. There is only one cycle and it takes 4 applications to get around, i.e. if you start at 1, you go to 2, then 3, then 4, and back to 1. This would be represented by x41. Another example is (1)(3)(24) for an r-orbit. There are two 1-cycles and one 2-cycle so it is represented as x12x21. Now here comes the real magic of this chart. If we take the sum of column 4 and divide it by the number of orbits in G (|G|=8) then we get the following equation:
B(x)=(x14+2x41+3x22+2x12x21)/8
A quick check will show how many unique colorings exist. Plug 2 (the number of colors) into the equation for all xp and you will get 6 which is what we found earlier! This equation can be used to determine the number of unique colorings possible with any n colors on a 2x2 square.
So what was described above was the basic approach to Burnside. We did it for a simple square but the process is just as easily done for a cube. The following link has an example of how to apply this process to a cube. But for the purpose of this page, we will just show the chart they give:
Just like the square, the first step is finding the elements of G. For a cube |G|=24. You then have to find the fixed rotations. They use the same form of notation that we used in the previous example to determine the number of n-cycles. By following the same exact steps as before, one gets the Burnside equation.
Polya
At first it is not easy to see what the real difference between Poyla and Burnside is and that is because Poyla is directly from Burnside's equation.
If we use the example from the 2x2 square, we start out with the equation for the number of unique colorings:B(x)=(x14+2x41+3x22+2x12x21)/8
Polya simply takes this equation and makes it so that it tells us more information about the colorings. It gives the number of colorings and make up of each unique coloring. This sounds confusing but it will be clearer in a little bit.
To obtain Polya, we take the individual xpn from column 4 make it equal to (t1p+t2p+...+tkp)n where ti is the ith color used on the graph. For our chart, we went with a 2-coloring: (bp+wp)n. If we do this for each value in column 4 and put the obtained value in column 1 then take a summation of these vaules and again, divide by |G| then we get the following equation:
P(b,w)= b4+b3w+2b2w2+bw3+w4
This shows that there is only one graph with four vertecies of color b, there are two graphs with two verticies of color b and two verticies of color w, and so on. This result matches our original results from the pictural proof at the begining of this article.
Definitions:
- Burnside-The lemma counts the number of orbits of a set X acted upon by a group G. # of Orbits = (1/|G|) Sum over G |x^g|. Where x^g is an element of x such that g(x) = x, and |x^G| is the number of elements that fit this defintion.
- Polya-Applies this to colors.
'
References and Additional Information
For further reading on the Polya theorem:
http://arxiv.org/pdf/1001.0072.pdf
http://math.berkeley.edu/~mbaker/Tucker.pdf
http://www.whitman.edu/mathematics/SeniorProjectArchive/2012/Huisinga.pdf
http://amininima.wordpress.com/2013/07/08/orbit-stabilizer-burnside-and-polya/
Back to MA375 Spring 2014