| Line 26: | Line 26: | ||
==Introduction== | ==Introduction== | ||
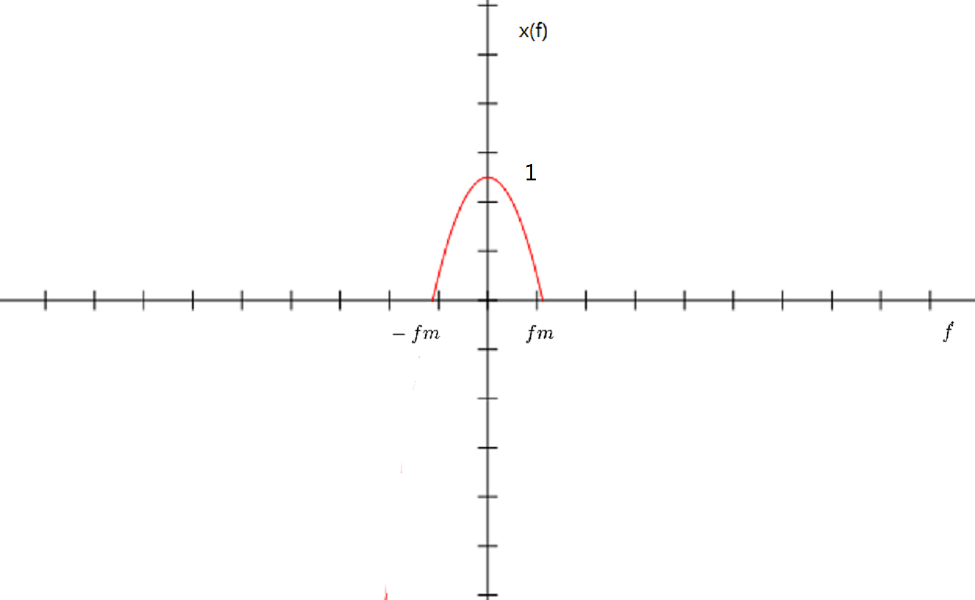
| − | + | <math> X(f) </math> (the CTFT of <math> x(t) </math> ), <math> X_s(f) </math> (the CTFT of <math> x_s(t) </math> ) <math> X_d(\omega) </math> (the DTFT of <math> x_d[n] </math> ) | |
---- | ---- | ||
==Derivation== | ==Derivation== | ||
| − | + | signal: <math> x_s(t) </math> and <math> x_d[n] </math>. <math> x_s(t) </math> <math> P_T(t) </math> with the original signal <math> x(t) </math> and actually <math> x_s(t) </math> is <math> comb_T(x(t)) </math> where T is the sampling period. | |
However the <math> x_d[n] </math> is <math> x(nT) </math> where T is the sampling period. | However the <math> x_d[n] </math> is <math> x(nT) </math> where T is the sampling period. | ||
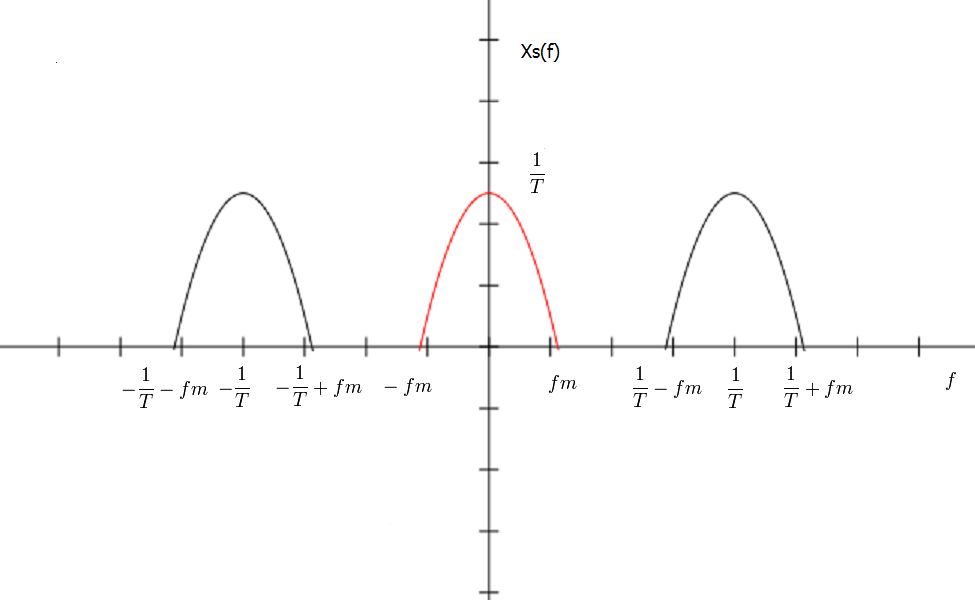
| − | + | relationship between <math> X(f) </math> and <math> X_s(f) </math>. | |
We know that <math> x_s(t) = x(t) \times P_T(t) </math>, we can derive the relationship between <math> x_s(t) </math> and <math> x(t) </math> in the following way: | We know that <math> x_s(t) = x(t) \times P_T(t) </math>, we can derive the relationship between <math> x_s(t) </math> and <math> x(t) </math> in the following way: | ||
| Line 65: | Line 65: | ||
==Derivation== | ==Derivation== | ||
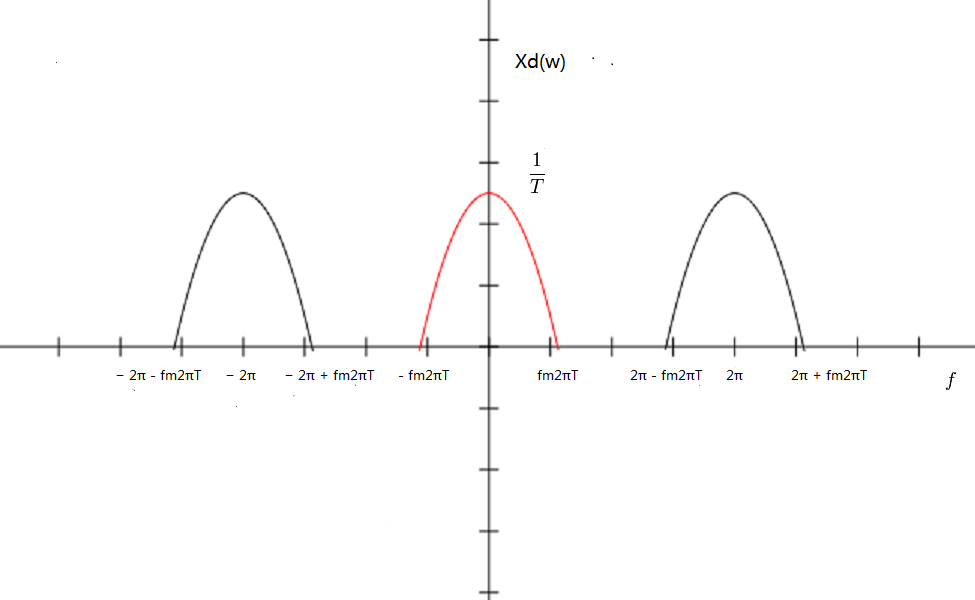
| − | + | n <math> X_s(f) </math> and <math> X_d(\omega) </math> | |
We know another way to express CTFT of <math> x_s(t) </math>: | We know another way to express CTFT of <math> x_s(t) </math>: | ||
| Line 116: | Line 116: | ||
<font size> | <font size> | ||
| − | + | ationship between <math> X_s(f) </math> and <math> X_d(\omega) </math> and the is showed in graph as below: | |
---- | ---- | ||
Revision as of 10:15, 9 October 2014
Frequency domain view of the relationship between a signal and a sampling of that signal
A slecture by ECE student Yerkebulan Yeshmukhanbetov
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Outline
- Introduction
- Derivation
- Example
- Conclusion
Introduction
$ X(f) $ (the CTFT of $ x(t) $ ), $ X_s(f) $ (the CTFT of $ x_s(t) $ ) $ X_d(\omega) $ (the DTFT of $ x_d[n] $ )
Derivation
signal: $ x_s(t) $ and $ x_d[n] $. $ x_s(t) $ $ P_T(t) $ with the original signal $ x(t) $ and actually $ x_s(t) $ is $ comb_T(x(t)) $ where T is the sampling period.
However the $ x_d[n] $ is $ x(nT) $ where T is the sampling period.
relationship between $ X(f) $ and $ X_s(f) $.
We know that $ x_s(t) = x(t) \times P_T(t) $, we can derive the relationship between $ x_s(t) $ and $ x(t) $ in the following way:
$ \begin{align} F(comb_T(x(t)) &= F(x(t) \times P_T(t))\\ &= X(f)*F(P_T(t))\\ &= X(f)*\frac{1}{T}\sum_{n = -\infty}^\infty \delta(f-\frac{n}{T})\\ &= \frac{1}{T}X(f)*P_\frac{1}{T}(f)\\ &= \frac{1}{T}rep_\frac{1}{T}X(f)\\ \end{align} $
Show this relationship in graph below:
example
Derivation
n $ X_s(f) $ and $ X_d(\omega) $
We know another way to express CTFT of $ x_s(t) $:
$ \begin{align} X_s(f) &= F(\sum_{n = -\infty}^\infty x(nT)\delta(t-nT))\\ &= \sum_{n = -\infty}^\infty x(nT)F(\delta(t-nT))\\ &= \sum_{n = -\infty}^\infty x(nT)e^{-j2\pi fnT}\\ \end{align} $
compare it with DTFT of $ x_d[n] $:
$ \begin{align} X_d(\omega) &= \sum_{n = -\infty}^\infty x_d[n]e^{-j\omega n}\\ &= \sum_{n = -\infty}^\infty x(nT)e^{-j\omega n}\\ \end{align} $
we can find that:
$ \begin{align} X_d(2\pi Tf) &= X_s(f)\\ \end{align} $
if $ f = \frac{1}{T} $
we have that:
$ \begin{align} X_d(2\pi ) &= X_s(\frac{1}{T})\\ \end{align} $
ationship between $ X_s(f) $ and $ X_d(\omega) $ and the is showed in graph as below:
example
conclusion
So the relationship between $ X(f) $ and $ X_s(f) $ is that $ X_s(f) $ is a a rep of $ X(f) $ in frequency domain with period of $ \frac{1}{T} $ and magnitude scaled by $ \frac{1}{T} $. the relationship between $ X(f) $ and $ X_d(\omega) $ is that $ X_d(\omega) $ is also a a rep of $ X(f) $ in frequency domain with period $ 2\pi $ and magnitude is also scaled by $ \frac{1}{T} $, but the frequency is scaled by $ 2\pi T $