(25 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
==Hypothesis Testing==
+
<br>
 +
<center><font size="4"></font>
 +
<font size="4">'''Neyman-Pearson: How Bayes Decision Rule Controls Error''' <br> </font> <font size="2">A [https://www.projectrhea.org/learning/slectures.php slecture] by Robert Ness </font>
  
−
'''模式识别''' 的目标是将新观察的特征向量进行分类。为了进行分类的决定，需要通过魔钟'''判决规则'''。在'''统计学模式识别'''我们假设特征向量'''是个随机变量“X”，又有个概率密度函数或者概率质量函数，并且此函数依赖其分类。如下假设有两个类型：<math>\omega_1,\omega_2</math>, 以便方便写公式也不失一般性。如此X的概率密度或概率质量函数是<math>P(X|\omega_i)</math>。每个类型的'''先验概率'''写成<math>P(\omega_i), i = 1,2</math>。
+
<font size="2">Partly based on the [[2014 Spring ECE 662 Boutin|ECE662 Spring 2014 lecture]] material of [[User:Mboutin|Prof. Mireille Boutin]]. </font>  
 +
</center>  
 +
----
  
−
统计学的主要部分之一是'''假设检验'''。下面描述假设检验在统计学模式识别的眼神。
 
  
−
Bayes Decision Rule for Minum Error
+
'''模式识别''' 的目标是将新观察的特征向量进行分类。为了进行分类的决定，需要通过魔钟'''判决规则(decision rule)'''。在 '''统计学模式识别''' 一般假设特征向量是个随机变量“X”，又有个概率密度函数或者概率质量函数，并且此函数依赖其分类。如下假设有两个类型：（<span class="texhtml">ω<sub>0</sub>,ω<sub>1</sub></span>）, 以便写公式也不失一般性。如此X的概率密度或质量函数是<span class="texhtml">''P''(''X'' | ω<sub>''i''</sub>)</span> (如下称pdf)。每个类型的'''先验概率'''写成<span class="texhtml">''P''(ω<sub>''i''</sub>)</span>。
−
假设X是个observation vector.
+
 
−
g_i(X) 是X 来自 omega_i 的 Posterior probability  
+
统计学的主要部分之一是'''假设检验'''。下面描述假设检验在统计学模式识别的眼神。
−
Decision rule: 如果 个g_1(X) > g_2(X),就选 omega1, 不然选 omega 2
+
 
−
据Bayes theorem, decision rule 可以用likelihood ratio 表示 <math> l(X) </math>
+
== 贝叶斯（Bayes)判决规则  ==
 +
 
 +
将<span class="texhtml">''g''<sub>''i''</sub>(''X'')</span> 是<span class="texhtml">ω<sub>''i''</sub></span>的'''后验概率(posterior probability)'''。选<span class="texhtml">ω<sub>1</sub></span>或<span class="texhtml">ω<sub>2</sub></span>的判决规则为: 如果<span class="texhtml">''g''<sub>0</sub>(''X'') &gt; ''g''<sub>1</sub>(''X'')</span>,就选<span class="texhtml">ω<sub>0</sub></span>, 不然选<span class="texhtml">ω<sub>1</sub></span>。据贝斯定理, 判决规则能以 '''似然比(likelihood ratio)'''<span class="texhtml">''0''(''X'')</span> 表示:
  
 
<math>\begin{align}
 
<math>\begin{align}
−
&  g_1(X) > g_2(X) \\
+
&  g_0(X) > g_1(X) \\
−
\Rightarrow & P(\omega_1|X) > P(\omega_2|X) \\
+
\Rightarrow & P(\omega_0|X) > P(\omega_1|X) \\
−
\Rightarrow &  \frac{P(X|\omega_1)P(\omega_1)}{P(X)} > \frac{P(X|\omega_2)P(\omega_2)}{P(X)} \\
+
\Rightarrow &  \frac{P(X|\omega_0)P(\omega_0)}{P(X)} > \frac{P(X|\omega_1)P(\omega_1)}{P(X)} \\
−
\Rightarrow & P(X|\omega_1)P(\omega_1) > P(X|\omega_2)P(\omega_2) \\
+
\Rightarrow & P(X|\omega_0)P(\omega_0) > P(X|\omega_1)P(\omega_1) \\
−
\Rightarrow & l(X)=\frac{P(X|\omega_1)}{P(X|\omega_2)} > \frac{P(\omega_2)}{P(\omega_1)} = k
+
\Rightarrow & l(X)=\frac{P(X|\omega_0)}{P(X|\omega_1)} > \frac{P(\omega_1)}{P(\omega_0)} = k
 
\end{align}
 
\end{align}
−
</math>
+
</math>  
  
−
k 是个constant， 而且，由于 <math> P(\omega_2) = 1 - P(\omega_1) </math>, k 可以看待是prior比值 : 。
+
k 是一位常数。贝叶斯（Bayes)判决规则就说明可以通过似然比与常数的比较进行决定。此手续叫做'''似然比检测(likelihood ratio test)'''。
 +
 
 +
== 贝叶斯错误 ==
 +
为了评估判决规则的效果，需要计算错误的概率。计算需要如下的记法定义：
 +
* <math>\epsilon_0</math> = P(错误选ω<sub>1</sub> ｜ ω<sub>0</sub>正确），<math>\epsilon_1</math> = P(错误选ω<sub>0</sub> ｜ ω<sub>1</sub>正确）
 +
* R<sub>i</sub>是选ω<sub>i</sub>的领域：<br><math>R_i=\{x\in X | choose \ \omega_i\}</math><br>
 +
* r(X)= min(g<sub>0</sub>(X),g<sub>1</sub>(X))。
 +
 
 +
 
 +
在贝叶斯决定规则下，错误几率等于'''贝叶斯错误几率(Bayes error rate)'''：
  
−
Bayes Error
 
−
为了评估我们的decision rule 的效果，需要计算probability of error
 
−
Define conditional error : <math> r(X) = min[g_1(X), g_2(X)] </math>
 
−
Define Bayes error:
 
 
<math>  
 
<math>  
−
\begin{align*}
+
\begin{align}
 
\\  
 
\\  
−
\epsilon & = E(r(X)) = \int min(P(\omega_1)P(X|\omega_1), P(\omega_2)P(X|\omega_2))dX \\
+
\epsilon_{Bayes} & = E(r(X)) = \int min(P(\omega_0)P(X|\omega_0), P(\omega_1)P(X|\omega1))dX \\
−
  &= P(\omega_1) \int_{R_2}P(X|\omega_1)dX + P(\omega_2) \int_{R_1} P(X|\omega_2)dX \\
+
  &= P(\omega_0) \int_{R_1}P(X|\omega_0)dX + P(\omega_1) \int_{R_0} P(X|\omega_1)dX \\
−
  &= P(\omega_1)\epsilon_1 + P(\omega_2)\epsilon_2
+
  &= P(\omega_0)\epsilon_0 + P(\omega_1)\epsilon_1
 
\end{align}
 
\end{align}
−
</math>
+
</math>  
−
以上的<math>R_i <\math> 定义为decision rule 决定选 <math> \omega_i <\math>的领域，然后 <math>\epsilon_i</math> 是<math>L_i<\math>选错的概率。
+
 
 +
==统计学假设检验的决定规则<br>  ==
 +
 
 +
如果你曾经上过入门的统计学课，你大概能想起传统的 '''假设检验'''. 如下为例子: <br>
 +
<blockquote>一位人类学研究者对一名太平岛部落，认为此部落预期寿命比一般人长。把 <span class="texhtml">μ</span> 定义为此部落预期寿命。全世界人口的预期寿命是67.2年。为了检验他的假设，他从公开记录随机选出了100个讣告作为随机样本,发现样本平均预期寿命是72，样本表春差是15。把 X̄ 定义为样本平均值，样本标准差 S，而且由于两都是来自随机样本，两都是随机变量。由于 然后用如下的假设检验:
 +
<br>
 +
零假设 (H0): <span class="texhtml">μ − 67.2 = 0</span>
 +
<br>
 +
对立假设(H1): <span class="texhtml">μ − 67.2 &gt; 0</span>
 +
<br>
 +
检验统计量: <math> T = \frac{\bar{X} - 67.5}{\sqrt{S^{2}/N}} \sim N(0,1) </math>.
 +
<br>
 +
决策规则: 若 <math> T < Z_{\alpha}  </math>  
 +
 
 +
则选H0不然选H1. </blockquote>
 +
 
 +
如上的H0、H1 、与α是传统的记法。α是 P(此判决规则让选H1 | H0正确)的上限。在这种检验，”H0正确但选H1“的错误叫做第一型错误。反而”H1正确但选H0“叫做第二型错误。所以 P(此判决规则让选H1 | H0正确)= P(第一型错误)。
 +
 
 +
'''这种假设检验最重要的特点是决定规则的目标是控制P(第一型错误)在α下。'''假如α＝.05。
 +
 
 +
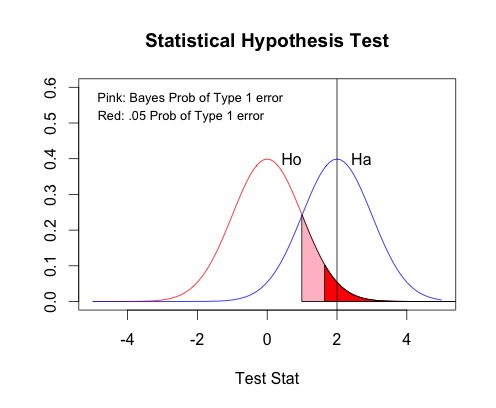
从统计学模式识别的角度上看此假设检验，H0 和 H1是两种类别 -- 可以换回原来的 “ω” 记法。随机特征向量是 T,而且条件pdf是高斯分布（标准正常密度分布）。研究者从T抽一次抽样值 t=（72 － 67.2）/(15 * 15 / 100) = 2。 各类的先验概率是平等的。如下图片显示两类的pdf。
 +
 
 +
'''[[Image:Rplot.png]]'''
 +
 
 +
粉红色的领域是在贝斯决定则下（平等先验概率）第一型错误的概率。红色的领域是固定在.05一下第一型错误的领域 -- 在标准正常分布就是高于1 - .05分位点 ＝ 高于1.644。贝斯的领域同时依赖<math> \omega_0 </math> 跟<math> \omega_1 </math>的分布 -- 具体说它依赖<math> \omega_0 </math>密度函数剪<math> \omega_1 </math>密度函数的根。但是如果只想控制第一型错误，只需要看<math> \omega_0 </math>分布。在这个检验，2 > 1.644, 决定规则让选H1.研究者大概要在他的论文宣告P值(显著性概率)为P(T>2| <math> \omega_0 </math> 正确）＝ 0.022，也就在是Ho的分布下2以上的曲线下面积。
 +
 
 +
这种检验的决定规则控制第一型错误的概率是为了避免在脆弱的证据下报道肯定的研究成果。它用如下的站落:
 +
*首先将P(第一型错误)＝ε<sub>0</sub> 固定在一定的数量α。
 +
*然后将P(第二型错误)＝ε<sub>1</sub>控制在尽可能少的数量。满足此条件的决定规则在统计学中叫做“一致最大功效检验(UMP test)”。
 +
 
 +
Neyman-Pearson引理：决定规则当UMP test的充分必要条件如下：
 +
<blockquote>
 +
<br>
 +
*ε<sub>0</sub>被固定在一位常数α然后决定规则是
 +
*如果<br>
 +
<math> l(T)=\frac{P(T| \omega_0 )}{P(T| \omega_1)} > k </math><br>
 +
    决定选<math> \omega_0 </math>
 +
*如果<br>
 +
<math> l(T)=\frac{P(T| \omega_0 )}{P(T|\omega_1 )} < k </math><br>
 +
    决定选<math> \omega_1 </math>。
 +
</blockquote>
 +
 
 +
==结论==
 +
传统的统计学假设检验的目标是将一个类别的错误概率固定在一定的水平下，然后尽可能减少另一个列别的错误概率。统计学假设检验认为一种错误要比另一种坏，但是贝叶斯决定规则给两种错误平等待遇。Neyman-Pearson 引理说明进行似然比检测是满足统计学假设检验的目标的目标的充分必要条件。不过贝叶斯决定规则毕竟就是似然比检测。所以贝叶斯决定规则的结果也就是固定一个类别的错误概率在一定的水平下，然后尽可能减少另一个列别的错误概率。
 +
 
 +
 
 +
----
 +
 
 +
== [[test_QnA|Questions and comments]]==
 +
 
 +
If you have any questions, comments, etc. please post them On [[test_QnA|this page]].
 +
 
 +
----
 +
 
  
−
Neyman-Pearson Test
+
[[2014_Spring_ECE_662_Boutin|Back to Spring 2014 ECE662 page]]
−
如果你曾经上过入门的统计学课，你大概能想起传统的 ** 假设检验 **. 如下为例子:
+
−
一位人类学研究生认为他所观察的两种部落有不同的各自高度。把<math>\mu_A <\math> 和 <math>\mu_B <\math>定义为 部落A和部落B的人均各自高度，所以等于说<math> \mu_A - \mu_B \neq 0 <\math>。为了检验他的假设，他就从不哦啰A和部落B随机性地选出了N个人的样本，然后两侧各人的各自高度，最后算了样本均值<math>\bar{X_A},\bar{X_B}<\math>和样本标准差<math>S_A^2，S_B^2</math>。然后用如下的假设检验.
+
−
零假设 (H0): <math> \mu_A - \mu_B = 0 <\math>
+
−
对立假设(Ha): <math> \mu_A - \mu_B \neq 0 <\math>
+
−
Test statistic: <math> T = \frac{\bar{X}_A - \bar{X}_B}{\sqrt{(S^2_A+S^2_B)/N}} </math>. 中心极限定理就让我们假设<math> T \sim N(0, 1) </math>.
+
−
Decision Rule: 若<math> T < Z_{\frac{\alpha}{2}} <\math> 或则 <math> T 》 Z_{\frac{1 － \alpha}{2}} <\math>，则选H0不然选Ha.
+
−
如上的<math>\alpha = P(判决规则让选Ha|H0正确)=P('''第一型錯誤''')</math>。反而'''第二型錯誤'''是判决规则让选H0|Ha正确.一般在这种假设检验，控制第一型錯誤的概率是最有限考虑。
+

Latest revision as of 19:30, 2 May 2014


Neyman-Pearson: How Bayes Decision Rule Controls Error
A slecture by Robert Ness

Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.


模式识别 的目标是将新观察的特征向量进行分类。为了进行分类的决定，需要通过魔钟判决规则(decision rule)。在 统计学模式识别 一般假设特征向量是个随机变量“X”，又有个概率密度函数或者概率质量函数，并且此函数依赖其分类。如下假设有两个类型：（ω0,ω1）, 以便写公式也不失一般性。如此X的概率密度或质量函数是P(X | ωi) (如下称pdf)。每个类型的先验概率写成P(ωi)。

统计学的主要部分之一是假设检验。下面描述假设检验在统计学模式识别的眼神。

贝叶斯（Bayes)判决规则

将gi(X) 是ωi的后验概率(posterior probability)。选ω1或ω2的判决规则为: 如果g0(X) > g1(X),就选ω0, 不然选ω1。据贝斯定理, 判决规则能以 似然比(likelihood ratio)0(X) 表示:

$ \begin{align} & g_0(X) > g_1(X) \\ \Rightarrow & P(\omega_0|X) > P(\omega_1|X) \\ \Rightarrow & \frac{P(X|\omega_0)P(\omega_0)}{P(X)} > \frac{P(X|\omega_1)P(\omega_1)}{P(X)} \\ \Rightarrow & P(X|\omega_0)P(\omega_0) > P(X|\omega_1)P(\omega_1) \\ \Rightarrow & l(X)=\frac{P(X|\omega_0)}{P(X|\omega_1)} > \frac{P(\omega_1)}{P(\omega_0)} = k \end{align} $

k 是一位常数。贝叶斯（Bayes)判决规则就说明可以通过似然比与常数的比较进行决定。此手续叫做似然比检测(likelihood ratio test)。

贝叶斯错误

为了评估判决规则的效果，需要计算错误的概率。计算需要如下的记法定义：

  • $ \epsilon_0 $ = P(错误选ω1 ｜ ω0正确），$ \epsilon_1 $ = P(错误选ω0 ｜ ω1正确）
  • Ri是选ωi的领域：
    $ R_i=\{x\in X | choose \ \omega_i\} $
  • r(X)= min(g0(X),g1(X))。


在贝叶斯决定规则下，错误几率等于贝叶斯错误几率(Bayes error rate)：

$ \begin{align} \\ \epsilon_{Bayes} & = E(r(X)) = \int min(P(\omega_0)P(X|\omega_0), P(\omega_1)P(X|\omega1))dX \\ &= P(\omega_0) \int_{R_1}P(X|\omega_0)dX + P(\omega_1) \int_{R_0} P(X|\omega_1)dX \\ &= P(\omega_0)\epsilon_0 + P(\omega_1)\epsilon_1 \end{align} $

统计学假设检验的决定规则

如果你曾经上过入门的统计学课，你大概能想起传统的 假设检验. 如下为例子:

一位人类学研究者对一名太平岛部落，认为此部落预期寿命比一般人长。把 μ 定义为此部落预期寿命。全世界人口的预期寿命是67.2年。为了检验他的假设，他从公开记录随机选出了100个讣告作为随机样本,发现样本平均预期寿命是72，样本表春差是15。把 X̄ 定义为样本平均值，样本标准差 S，而且由于两都是来自随机样本，两都是随机变量。由于 然后用如下的假设检验:


零假设 (H0): μ − 67.2 = 0
对立假设(H1): μ − 67.2 > 0
检验统计量: $ T = \frac{\bar{X} - 67.5}{\sqrt{S^{2}/N}} \sim N(0,1) $.
决策规则: 若 $ T < Z_{\alpha} $

则选H0不然选H1.

如上的H0、H1 、与α是传统的记法。α是 P(此判决规则让选H1 | H0正确)的上限。在这种检验，”H0正确但选H1“的错误叫做第一型错误。反而”H1正确但选H0“叫做第二型错误。所以 P(此判决规则让选H1 | H0正确)= P(第一型错误)。

这种假设检验最重要的特点是决定规则的目标是控制P(第一型错误)在α下。假如α＝.05。

从统计学模式识别的角度上看此假设检验，H0 和 H1是两种类别 -- 可以换回原来的 “ω” 记法。随机特征向量是 T,而且条件pdf是高斯分布（标准正常密度分布）。研究者从T抽一次抽样值 t=（72 － 67.2）/(15 * 15 / 100) = 2。 各类的先验概率是平等的。如下图片显示两类的pdf。

Rplot.png

粉红色的领域是在贝斯决定则下（平等先验概率）第一型错误的概率。红色的领域是固定在.05一下第一型错误的领域 -- 在标准正常分布就是高于1 - .05分位点 ＝ 高于1.644。贝斯的领域同时依赖$ \omega_0 $ 跟$ \omega_1 $的分布 -- 具体说它依赖$ \omega_0 $密度函数剪$ \omega_1 $密度函数的根。但是如果只想控制第一型错误，只需要看$ \omega_0 $分布。在这个检验，2 > 1.644, 决定规则让选H1.研究者大概要在他的论文宣告P值(显著性概率)为P(T>2| $ \omega_0 $ 正确）＝ 0.022，也就在是Ho的分布下2以上的曲线下面积。

这种检验的决定规则控制第一型错误的概率是为了避免在脆弱的证据下报道肯定的研究成果。它用如下的站落:

  • 首先将P(第一型错误)＝ε0 固定在一定的数量α。
  • 然后将P(第二型错误)＝ε1控制在尽可能少的数量。满足此条件的决定规则在统计学中叫做“一致最大功效检验(UMP test)”。

Neyman-Pearson引理：决定规则当UMP test的充分必要条件如下：


  • ε0被固定在一位常数α然后决定规则是
  • 如果

$ l(T)=\frac{P(T| \omega_0 )}{P(T| \omega_1)} > k $
决定选$ \omega_0 $

  • 如果

$ l(T)=\frac{P(T| \omega_0 )}{P(T|\omega_1 )} < k $
决定选$ \omega_1 $。

结论

传统的统计学假设检验的目标是将一个类别的错误概率固定在一定的水平下，然后尽可能减少另一个列别的错误概率。统计学假设检验认为一种错误要比另一种坏，但是贝叶斯决定规则给两种错误平等待遇。Neyman-Pearson 引理说明进行似然比检测是满足统计学假设检验的目标的目标的充分必要条件。不过贝叶斯决定规则毕竟就是似然比检测。所以贝叶斯决定规则的结果也就是固定一个类别的错误概率在一定的水平下，然后尽可能减少另一个列别的错误概率。


Questions and comments

If you have any questions, comments, etc. please post them On this page.


Back to Spring 2014 ECE662 page

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=NeymanPearson中文Spring2014&oldid=65226"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

has a message for current ECE438 students.

Sean Hu, ECE PhD 2009