| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 9, [[ECE662]]: Decision Theory= |
| − | [ | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. |
| − | ' | + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], |
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| − | + | '''Parametric Methods''' | |
| − | + | ||
| − | |||
| − | |||
Two applications: | Two applications: | ||
| − | + | * Parametric Density Estimation: Using sample data, we estimate probabilities <math>P(\omega_i)</math>, <math>p(\vec{X}|\omega_i) \forall i</math> etc using estimation methods like [[MLE_Old Kiwi]] and [[BPE_Old Kiwi]]. Then from these estimated probabilities (and not true probabilities, which are unknown; only their parametric form was known) we can use Bayes classification rule to build a classifier. | |
| − | + | * [[Parametric Classifiers_Old Kiwi]]: We find parametric decision boundaries to approximate true decision boundaries between classes. This is very different approach from approximating the probabilities with their estimates, as in previous method. | |
| − | Example: | + | Example: |
| + | [[Image:Lecture9_parametric_decion_boundary_Old Kiwi.JPG]] | ||
.. image:: Lecture9_parametric_decion_boundary.JPG | .. image:: Lecture9_parametric_decion_boundary.JPG | ||
| − | + | True decision boundary: <math> \{\vec{X}|P(\omega_1|\vec{X})-P(\omega_2|\vec{X})=0\}</math> can be approximated by <math>\{\vec{X}|g(\vec{X})=0\}</math>. Note that 'g' is not an estimate of the difference in probabilities as in true decision boundary, but it is just an approximate parametric form for the true decision boundary. Choice of 'g' depends on whether it is analytic, and hence easy to handle computationally. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
E.g. 'g' can be a degree-2 polynomial, or it can be a degree-1 polynomial (resulting in a linear classifier). | E.g. 'g' can be a degree-2 polynomial, or it can be a degree-1 polynomial (resulting in a linear classifier). | ||
| − | + | If 'g' is linear, it can be written as <math>g(\vec{X})=\vec{V}\cdot \vec{X}+V_0=(\vec{V},V_0)\cdot (\vec{X},1)</math> or <math>g(1,\vec{X})=\vec{c}\cdot(1,\vec{X})</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''Extension of Feature Space:''' | |
This trick justifies the importance of studying linear classifiers even though they do not occur so often in practice directly. Actually, many non-linear classifiers can be seen as linear. | This trick justifies the importance of studying linear classifiers even though they do not occur so often in practice directly. Actually, many non-linear classifiers can be seen as linear. | ||
| − | + | Example 1: Consider g to be a polynomial parametric form of a classifier in <math>\mathbb{R}^2</math>. | |
| − | + | ||
| − | + | <math> g(x,y)=c_0+c_1x+c_2y+c_3xy+c_4{x}^2+c_5{y}^2 </math> | |
| − | + | ||
| − | + | Here g is not a linear classifier in <math>\mathbb{R}^2</math>. Let us define <math>\tilde{g}:\mathbb{R}^5 \to \mathbb{R}</math> | |
| − | + | <math> \tilde{g}(u_1,u_2,u_3,u_4,u_5)=c_0+c_1u_1+c_2u_2+c_3u_3+c_4u_4+c_5u_5 </math> | |
| − | + | where <math> u_1=x; u_2=y; u_3=xy; u_4={x}^2; u_5={y}^2 </math>. Here we have defined a parametric from of the classifier in extended feature space. This form is linear. Hence "Decision boundary defined by 'g' is linear in extended feature space." | |
| − | + | ||
| − | + | Example 2: Consider another polynomial, | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math> g(x)={x}^2+{y}^2-2{y} = {x}^2+{(y-1)}^2 -1 </math> | |
| − | + | This is a circle centred at (0,1): | |
| − | + | ||
| − | + | ||
| − | This is a circle centred at (0,1): | + | |
| − | + | [[Image:Circle_Old Kiwi.jpg]] | |
This non-linear function can be transformed into linear function in extended feature space like below. | This non-linear function can be transformed into linear function in extended feature space like below. | ||
| − | + | <math> \{ (x, y, x^2, y^2) \mid (0, -2, 1, 1) \cdot (x, y, x^2, y^2) = 0 \} </math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | [[Image:lec9_embedd_Old Kiwi.jpg]] | ||
Example 3: 1D example | Example 3: 1D example | ||
| − | + | [[Image:Jinha_1D_Example01_Old Kiwi.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | As we can see from above figure, decision boundary is not linear (region is not connected). From this, we can construct an extended [feature vector] space. | |
| − | + | <math> x \rightarrow (x, x^2) \in R^2 </math> | |
| − | + | ||
| − | + | [[Image:Jinha_1D_Example02_Old Kiwi.jpg]] | |
This red line (which is a hyperplane in this case) can separate these two classes. | This red line (which is a hyperplane in this case) can separate these two classes. | ||
This can be expressed as below mathematical form. | This can be expressed as below mathematical form. | ||
| − | + | <math> p(x \mid w_1) \rightarrow p(x, x^2 \mid w_1) </math> | |
| − | + | '''Taylor Series:''' If true <math>\vec{g}</math> is analytic | |
| − | + | e.g <math> g(\vec{X})=\sum_{i=1}^{n}{\lambda}_{i}{e}^{{c}_{i}\vec{x}} </math> | |
| − | + | then, <math> g(\vec{x}) </math> = Taylor Series --> infinite polynomial in powers | |
| − | + | ||
| − | + | because we can approximate with Taylor polynomial of degree n | |
| − | + | (i.e as n get higher, approximation gets better) | |
| − | + | [[Image:poly2_Old Kiwi.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
However, there are issues on this approach. It gets complex with the increase of the dimension of the [feature vector]. | However, there are issues on this approach. It gets complex with the increase of the dimension of the [feature vector]. | ||
| − | If | + | If <math> \vec{x} = (x_1, x_2, \cdots, x_d) </math> |
| − | + | A degree 2 polynomial in <math> \vec{x} = (x_1, x_2, \cdots, x_d) </math> has <math> \frac{1}{2} (d+1) (d+2) \approx d^2 </math> monomials | |
| − | + | ||
| − | A degree | + | A degree n polynomial in <math> \vec{x} = (x_1, x_2, \cdots, x_d) </math> has <math> \approx d^n </math> monomials. |
| − | + | '''How to find decision hyperplane given training data''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
In the best of all cases, data is "linearly separable", meaning there exists a vector c such that for all y training data: | In the best of all cases, data is "linearly separable", meaning there exists a vector c such that for all y training data: | ||
| Line 152: | Line 120: | ||
c * y < 0 of u belongs to class w2. | c * y < 0 of u belongs to class w2. | ||
| − | + | '''Trick:''' replace all y's in the training data belonging to class w2 by -y, then look for vector c such that | |
c * y > 0 for all y. | c * y > 0 for all y. | ||
| − | |||
Example: 1D feature space | Example: 1D feature space | ||
| Line 160: | Line 127: | ||
x->(1,x)=:y | x->(1,x)=:y | ||
| − | + | [[Image:Lecture9_1D_yi_-yi_Old Kiwi.JPG]] | |
First component is +1 for all of class 1 training data | First component is +1 for all of class 1 training data | ||
| Line 166: | Line 133: | ||
First component is -1 for all of class 2 training data | First component is -1 for all of class 2 training data | ||
| − | + | [[Image:Lecture9_1D_yi_-yi_2_Old Kiwi.JPG]] | |
Observe: c is not unique | Observe: c is not unique | ||
| − | To make | + | To make <math> \vec{c} </math> unique, introduce 'margin' b>0 and ask that c be the minimum length vector such that <math> \vec{c} \cdot y_{i} \geq b </math>, for all i |
| − | + | '''Geometric Interpretation of margin''' | |
| − | + | ||
| − | + | If <math> \vec{c} \cdot y_{i} = b </math>, then <math> \vec{c} </math> belongs to hyperplane with normal vector <math> y_{i0} </math> which is at distance <math> \displaystyle \frac{b} {\displaystyle ||y_{i0} ||} </math> from the origin. | |
| − | + | ||
| − | |||
| − | + | <math> \vec{c} \cdot y_{i} \geq b </math>, for all i means that <math> \vec{c} </math> is always at least a distance <math> \displaystyle \frac{b} {\displaystyle ||y_{i0} ||} </math> from the origin for all i | |
| − | + | In general, it is impossible to satisfy <math>\vec{c} \cdot y_{i} \geq 0 </math>, for all i | |
| − | + | ||
| − | + | Perhaps, we could try to minimize number of misclassfied training samples | |
| − | + | ||
| − | + | Let <math> J(\vec{c})=\{ y_{i} | \vec{c} \cdot y_{i} \leq 0 \} </math> -> Too hard to minimize. | |
| − | + | ||
| − | + | '''[[Perceptron_Old Kiwi]] Criterion function''' | |
| − | + | <math> J_{p}(\vec{c})=\displaystyle \sum_{y_i, missclassified} (- \vec{c} \cdot y_{i} ) </math> | |
| − | + | [[Image:lec9_percept_Old Kiwi.JPG]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Measure how 'far away' you are from bias right. | Measure how 'far away' you are from bias right. | ||
| − | distance from |y_i| to hyperplane defined by |vec_c| is | + | distance from |y_i| to hyperplane defined by |vec_c| is <math> ||\vec{y_i} \cdot \frac{\vec{c}}{||\vec{c}||} ||=\frac{1}{|| \vec{c} ||} \vec{y_i} \cdot \vec{c} </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Since <math> \vec{c} \cdot \vec{y} </math> is proportional to distance from <math> y_{i} </math> to hyperplane | ||
| − | + | [[Category:Lecture Notes]] | |
| − | + | ||
Latest revision as of 08:48, 17 January 2013
Lecture 9, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Parametric Methods
Two applications:
- Parametric Density Estimation: Using sample data, we estimate probabilities $ P(\omega_i) $, $ p(\vec{X}|\omega_i) \forall i $ etc using estimation methods like MLE_Old Kiwi and BPE_Old Kiwi. Then from these estimated probabilities (and not true probabilities, which are unknown; only their parametric form was known) we can use Bayes classification rule to build a classifier.
- Parametric Classifiers_Old Kiwi: We find parametric decision boundaries to approximate true decision boundaries between classes. This is very different approach from approximating the probabilities with their estimates, as in previous method.
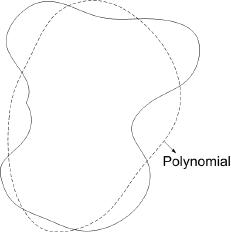
Example:
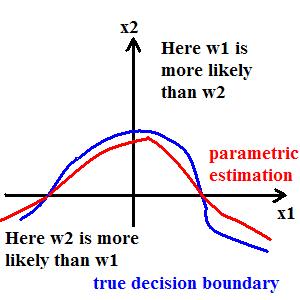
True decision boundary: $ \{\vec{X}|P(\omega_1|\vec{X})-P(\omega_2|\vec{X})=0\} $ can be approximated by $ \{\vec{X}|g(\vec{X})=0\} $. Note that 'g' is not an estimate of the difference in probabilities as in true decision boundary, but it is just an approximate parametric form for the true decision boundary. Choice of 'g' depends on whether it is analytic, and hence easy to handle computationally.
E.g. 'g' can be a degree-2 polynomial, or it can be a degree-1 polynomial (resulting in a linear classifier).
If 'g' is linear, it can be written as $ g(\vec{X})=\vec{V}\cdot \vec{X}+V_0=(\vec{V},V_0)\cdot (\vec{X},1) $ or $ g(1,\vec{X})=\vec{c}\cdot(1,\vec{X}) $.
Extension of Feature Space: This trick justifies the importance of studying linear classifiers even though they do not occur so often in practice directly. Actually, many non-linear classifiers can be seen as linear.
Example 1: Consider g to be a polynomial parametric form of a classifier in $ \mathbb{R}^2 $.
$ g(x,y)=c_0+c_1x+c_2y+c_3xy+c_4{x}^2+c_5{y}^2 $
Here g is not a linear classifier in $ \mathbb{R}^2 $. Let us define $ \tilde{g}:\mathbb{R}^5 \to \mathbb{R} $
$ \tilde{g}(u_1,u_2,u_3,u_4,u_5)=c_0+c_1u_1+c_2u_2+c_3u_3+c_4u_4+c_5u_5 $
where $ u_1=x; u_2=y; u_3=xy; u_4={x}^2; u_5={y}^2 $. Here we have defined a parametric from of the classifier in extended feature space. This form is linear. Hence "Decision boundary defined by 'g' is linear in extended feature space."
Example 2: Consider another polynomial,
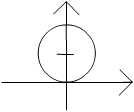
$ g(x)={x}^2+{y}^2-2{y} = {x}^2+{(y-1)}^2 -1 $
This is a circle centred at (0,1):
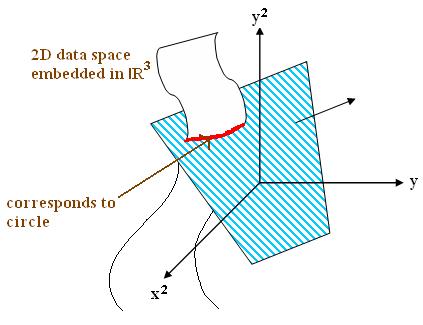
This non-linear function can be transformed into linear function in extended feature space like below.
$ \{ (x, y, x^2, y^2) \mid (0, -2, 1, 1) \cdot (x, y, x^2, y^2) = 0 \} $
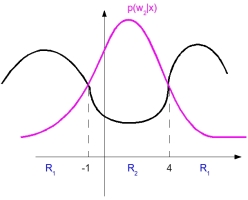
Example 3: 1D example
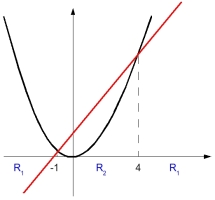
As we can see from above figure, decision boundary is not linear (region is not connected). From this, we can construct an extended [feature vector] space.
$ x \rightarrow (x, x^2) \in R^2 $
This red line (which is a hyperplane in this case) can separate these two classes. This can be expressed as below mathematical form.
$ p(x \mid w_1) \rightarrow p(x, x^2 \mid w_1) $
Taylor Series: If true $ \vec{g} $ is analytic e.g $ g(\vec{X})=\sum_{i=1}^{n}{\lambda}_{i}{e}^{{c}_{i}\vec{x}} $
then, $ g(\vec{x}) $ = Taylor Series --> infinite polynomial in powers
because we can approximate with Taylor polynomial of degree n (i.e as n get higher, approximation gets better)
However, there are issues on this approach. It gets complex with the increase of the dimension of the [feature vector].
If $ \vec{x} = (x_1, x_2, \cdots, x_d) $
A degree 2 polynomial in $ \vec{x} = (x_1, x_2, \cdots, x_d) $ has $ \frac{1}{2} (d+1) (d+2) \approx d^2 $ monomials
A degree n polynomial in $ \vec{x} = (x_1, x_2, \cdots, x_d) $ has $ \approx d^n $ monomials.
How to find decision hyperplane given training data
In the best of all cases, data is "linearly separable", meaning there exists a vector c such that for all y training data: c * y > 0 if y belongs to class w1. (where * is a dot product) c * y < 0 of u belongs to class w2.
Trick: replace all y's in the training data belonging to class w2 by -y, then look for vector c such that c * y > 0 for all y.
Example: 1D feature space
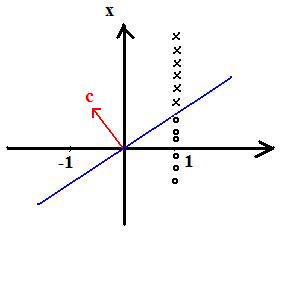
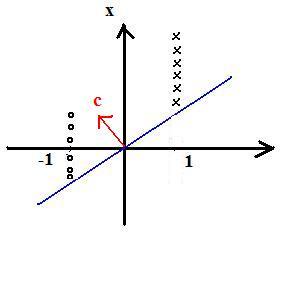
x->(1,x)=:y
First component is +1 for all of class 1 training data
First component is -1 for all of class 2 training data
Observe: c is not unique
To make $ \vec{c} $ unique, introduce 'margin' b>0 and ask that c be the minimum length vector such that $ \vec{c} \cdot y_{i} \geq b $, for all i
Geometric Interpretation of margin
If $ \vec{c} \cdot y_{i} = b $, then $ \vec{c} $ belongs to hyperplane with normal vector $ y_{i0} $ which is at distance $ \displaystyle \frac{b} {\displaystyle ||y_{i0} ||} $ from the origin.
$ \vec{c} \cdot y_{i} \geq b $, for all i means that $ \vec{c} $ is always at least a distance $ \displaystyle \frac{b} {\displaystyle ||y_{i0} ||} $ from the origin for all i
In general, it is impossible to satisfy $ \vec{c} \cdot y_{i} \geq 0 $, for all i
Perhaps, we could try to minimize number of misclassfied training samples
Let $ J(\vec{c})=\{ y_{i} | \vec{c} \cdot y_{i} \leq 0 \} $ -> Too hard to minimize.
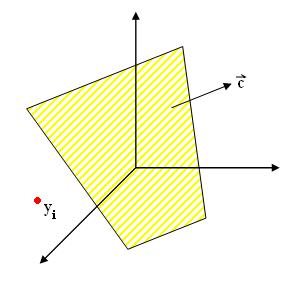
Perceptron_Old Kiwi Criterion function
$ J_{p}(\vec{c})=\displaystyle \sum_{y_i, missclassified} (- \vec{c} \cdot y_{i} ) $
Measure how 'far away' you are from bias right. distance from |y_i| to hyperplane defined by |vec_c| is $ ||\vec{y_i} \cdot \frac{\vec{c}}{||\vec{c}||} ||=\frac{1}{|| \vec{c} ||} \vec{y_i} \cdot \vec{c} $
Since $ \vec{c} \cdot \vec{y} $ is proportional to distance from $ y_{i} $ to hyperplane