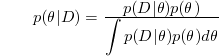| (17 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 7, [[ECE662]]: Decision Theory= |
| − | [ | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. |
| − | == Lecture | + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], |
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| + | == Lecture Content == | ||
* Maximum Likelihood Estimation and Bayesian Parameter Estimation | * Maximum Likelihood Estimation and Bayesian Parameter Estimation | ||
* Parametric Estimation of Class Conditional Density | * Parametric Estimation of Class Conditional Density | ||
| − | + | == Relevant Links== | |
| − | + | *MLE: [[Maximum Likelihood Estimation_Old Kiwi| Maximum Likelihood Estimation]] | |
| + | **[[MLE Examples: Exponential and Geometric Distributions_Old Kiwi|Examples of MLE: Exponential and Geometric Distributions ]] | ||
| + | **[[MLE Examples: Binomial and Poisson Distributions_Old Kiwi|Examples of MLE: Binomial and Poisson Distributions]] | ||
| + | *BPE: [[Bayesian Parameter Estimation_Old Kiwi|Bayesian Parameter Estimation]] | ||
| + | *[[Comparison of MLE and Bayesian Parameter Estimation_Old Kiwi|Comparison of MLE and Bayesian Parameter Estimation]] | ||
| + | *[[Parametric Estimators_Old Kiwi|Parametric Estimators]] | ||
| + | ---- | ||
| + | ----- | ||
The class conditional density <math>p(\vec{x}|w_i)</math> can be estimated using training data. We denote the parameter of estimation as <math>\vec{\theta}</math>. There are two methods of estimation discussed. | The class conditional density <math>p(\vec{x}|w_i)</math> can be estimated using training data. We denote the parameter of estimation as <math>\vec{\theta}</math>. There are two methods of estimation discussed. | ||
| − | MLE | + | MLE: [[Maximum Likelihood Estimation_Old Kiwi| Maximum Likelihood Estimation]] |
| − | BPE | + | BPE: [[Bayesian Parameter Estimation_Old Kiwi|Bayesian Parameter Estimation]] |
| Line 29: | Line 66: | ||
<math>p(\vec{X}|\omega_i,\vec{\theta_i})</math> equals <math>p(\vec{X}|\vec{\theta})</math> for a single class. | <math>p(\vec{X}|\omega_i,\vec{\theta_i})</math> equals <math>p(\vec{X}|\vec{\theta})</math> for a single class. | ||
| − | The | + | The ''Likelihood Function'' is, then, defined as <math>p(D|\vec{\theta})=\displaystyle \prod_{k=1}^n p(\vec{X_k}|\vec{\theta})</math>, |
which needs to be maximized for obtaining the parameter. | which needs to be maximized for obtaining the parameter. | ||
| − | |||
| − | |||
Since logarithm is a monotonic function, maximizing the Likelihood is same as maximizing log of Likelihood which is defined as | Since logarithm is a monotonic function, maximizing the Likelihood is same as maximizing log of Likelihood which is defined as | ||
| Line 48: | Line 83: | ||
Let <math>\vec{\theta} = \left[ \theta_1, \theta_2, \cdots , \theta_p \right]</math> be 1 by p vector, then | Let <math>\vec{\theta} = \left[ \theta_1, \theta_2, \cdots , \theta_p \right]</math> be 1 by p vector, then | ||
| − | <math>\nabla_{\vec{\theta}} = \left[ \frac{\partial}{\partial\theta_1} | + | <math>\nabla_{\vec{\theta}} = \left[ \frac{\partial}{\partial\theta_1} \frac{\partial}{\partial\theta_2} \cdots \frac{\partial}{\partial\theta_p} \right]^{t}</math> |
Then, we can compute the first derivatives of log likelyhood function, | Then, we can compute the first derivatives of log likelyhood function, | ||
| Line 57: | Line 92: | ||
<math>\rightarrow \nabla_{\vec{\theta}} ( l (\vec{\theta}) ) = 0</math> | <math>\rightarrow \nabla_{\vec{\theta}} ( l (\vec{\theta}) ) = 0</math> | ||
| − | |||
== Example of Guassian case == | == Example of Guassian case == | ||
| − | Assume that covariance matrix are | + | Assume that covariance matrix are known. |
<math>p(\vec{x_k} | \vec{\mu}) = \frac{1}{ \left( (2\pi)^{d} |\Sigma| \right)^{\frac{1}{2}}} exp \left[ - \frac{1}{2} (\vec{x_k} - \vec{\mu})^{t} \Sigma^{-1} (\vec{x_k} - \vec{\mu}) \right]</math> | <math>p(\vec{x_k} | \vec{\mu}) = \frac{1}{ \left( (2\pi)^{d} |\Sigma| \right)^{\frac{1}{2}}} exp \left[ - \frac{1}{2} (\vec{x_k} - \vec{\mu})^{t} \Sigma^{-1} (\vec{x_k} - \vec{\mu}) \right]</math> | ||
| Line 85: | Line 119: | ||
This is the sample mean for a sample size n. | This is the sample mean for a sample size n. | ||
| − | [[MLE Examples: Exponential and Geometric Distributions_Old Kiwi]] | + | [[MLE Examples: Exponential and Geometric Distributions_Old Kiwi|Examples of MLE: Exponential and Geometric Distributions ]] |
| − | [[MLE Examples: Binomial and Poisson Distributions_Old Kiwi]] | + | [[MLE Examples: Binomial and Poisson Distributions_Old Kiwi|Examples of MLE: Binomial and Poisson Distributions]] |
'''Advantages of MLE:''' | '''Advantages of MLE:''' | ||
| Line 93: | Line 127: | ||
* Converges | * Converges | ||
* Asymptotically unbiased (though biased for small N) | * Asymptotically unbiased (though biased for small N) | ||
| − | |||
== Bayesian Parameter Estimation == | == Bayesian Parameter Estimation == | ||
For a given class, | For a given class, | ||
| − | let <math> | + | let <b><math>x</math></b> be feature vector of the class and <b><math>\theta</math></b> be parameter of pdf of <b><math>x</math></b> to be estimated. |
| − | And let <math>D= \{ | + | And let <b><math>D= \{ x_1, x_2, \cdots, x_n \} </math></b> |
| − | , where <math> | + | , where <b><math>x</math></b> are training samples of the class |
| − | Note that <math> | + | Note that <b><math>\theta</math></b> is random variable with probability density <b><math>p(\theta)</math></b> |
| − | + | [[Image:Equation1_Old Kiwi.png]] | |
where | where | ||
| − | + | [[Image:Equation2_Old Kiwi.png]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== EXAMPLE: Bayesian Inference for Gaussian Mean == | == EXAMPLE: Bayesian Inference for Gaussian Mean == | ||
| Line 145: | Line 173: | ||
The above figure illustrates the Bayesian inference for the mean of a Gaussian distribution, for which the variance is assumed to be known. The curves show the prior distribution over 'mu' (the curve labeled N=0), which in this case is itself Gaussian, along with the posterior distributions for increasing number N of data points. The figure makes clear that as the number of data points increase, the posterior distribution peaks around the true value of the mean. This phenomenon is known as *Bayesian learning*. | The above figure illustrates the Bayesian inference for the mean of a Gaussian distribution, for which the variance is assumed to be known. The curves show the prior distribution over 'mu' (the curve labeled N=0), which in this case is itself Gaussian, along with the posterior distributions for increasing number N of data points. The figure makes clear that as the number of data points increase, the posterior distribution peaks around the true value of the mean. This phenomenon is known as *Bayesian learning*. | ||
| + | ---- | ||
| + | ---- | ||
| + | ==For more information== | ||
| − | + | *MLE: [[Maximum Likelihood Estimation_Old Kiwi| Maximum Likelihood Estimation]] | |
| + | **[[MLE Examples: Exponential and Geometric Distributions_Old Kiwi|Examples of MLE: Exponential and Geometric Distributions ]] | ||
| + | **[[MLE Examples: Binomial and Poisson Distributions_Old Kiwi|Examples of MLE: Binomial and Poisson Distributions]] | ||
| + | *BPE: [[Bayesian Parameter Estimation_Old Kiwi|Bayesian Parameter Estimation]] | ||
| + | *[[Comparison of MLE and Bayesian Parameter Estimation_Old Kiwi|Comparison of MLE and Bayesian Parameter Estimation]] | ||
| + | *[[Parametric Estimators_Old Kiwi|Parametric Estimators]] | ||
| + | ---- | ||
| + | [[ECE662:BoutinSpring08_Old_Kiwi|Back to ECE662, Spring 2008, Prof. Boutin]] | ||
| − | [[ | + | [[Category:lecture notes]] |
Latest revision as of 10:16, 20 May 2013
Contents
Lecture 7, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Lecture Content
- Maximum Likelihood Estimation and Bayesian Parameter Estimation
- Parametric Estimation of Class Conditional Density
Relevant Links
- MLE: Maximum Likelihood Estimation
- BPE: Bayesian Parameter Estimation
- Comparison of MLE and Bayesian Parameter Estimation
- Parametric Estimators
The class conditional density $ p(\vec{x}|w_i) $ can be estimated using training data. We denote the parameter of estimation as $ \vec{\theta} $. There are two methods of estimation discussed.
MLE: Maximum Likelihood Estimation
BPE: Bayesian Parameter Estimation
Maximum Likelihood Estimation
Let "c" denote the number of classes. D, the entire collection of sample data. $ D_1, \ldots, D_c $ represent the classification of data into classes $ \omega_1, \ldots, \omega_c $. It is assumed that: - Samples in $ D_i $ give no information about the samples in $ D_j, i \neq j $, and - Each sample is drawn independently.
Example: The class conditional density $ p(\vec{x}|w_i) $ depends on parameter $ \vec{\theta_i} $. If $ X ~ N(\mu,\sigma^2) $ denotes the class conditional density; then $ \vec{\theta}=[\mu,\sigma^2] $.
Let n be the size of training sample, and $ D=\{\vec{X_1}, \ldots, \vec{X_n}\} $. Then,
$ p(\vec{X}|\omega_i,\vec{\theta_i}) $ equals $ p(\vec{X}|\vec{\theta}) $ for a single class.
The Likelihood Function is, then, defined as $ p(D|\vec{\theta})=\displaystyle \prod_{k=1}^n p(\vec{X_k}|\vec{\theta}) $, which needs to be maximized for obtaining the parameter.
Since logarithm is a monotonic function, maximizing the Likelihood is same as maximizing log of Likelihood which is defined as
$ l(\vec{\theta})=log p(D|\vec{\theta})=\displaystyle log(\prod_{k=1}^n p(\vec{X_k}|\vec{\theta}))=\displaystyle \sum_{k=1}^n log(p(\vec{X_k}|\vec{\theta})) $.
"l" is the log likelihood function.
Maximize log likelyhood function with respect to $ \vec{\theta} $
$ \rightarrow \hat{\theta} = argmax \left( l (\vec{\theta}) \right) $
If $ l(\vec{\theta}) $ is a differentiable function
Let $ \vec{\theta} = \left[ \theta_1, \theta_2, \cdots , \theta_p \right] $ be 1 by p vector, then
$ \nabla_{\vec{\theta}} = \left[ \frac{\partial}{\partial\theta_1} \frac{\partial}{\partial\theta_2} \cdots \frac{\partial}{\partial\theta_p} \right]^{t} $
Then, we can compute the first derivatives of log likelyhood function,
$ \rightarrow \nabla_{\vec{\theta}} ( l (\vec{\theta}) ) = \sum_{k=1}^{n} \nabla_{\vec{\theta}} \left[ log(p(\vec{x_k} | \vec{\theta})) \right] $
and equate this first derivative to be zero
$ \rightarrow \nabla_{\vec{\theta}} ( l (\vec{\theta}) ) = 0 $
Example of Guassian case
Assume that covariance matrix are known.
$ p(\vec{x_k} | \vec{\mu}) = \frac{1}{ \left( (2\pi)^{d} |\Sigma| \right)^{\frac{1}{2}}} exp \left[ - \frac{1}{2} (\vec{x_k} - \vec{\mu})^{t} \Sigma^{-1} (\vec{x_k} - \vec{\mu}) \right] $
Step 1: Take log
$ log p(\vec{x_k} | \vec{\mu}) = -\frac{1}{2} log \left( (2\pi)^d |\Sigma| \right) - \frac{1}{2} (\vec{x_k} - \vec{\mu})^{t} \Sigma^{-1} (\vec{x_k} - \vec{\mu}) $
Step 2: Take derivative
$ \frac{\partial}{\partial\vec{\mu}} \left( log p(\vec{x_k} | \vec{\mu}) \right) = \frac{1}{2} \left[ (\vec{x_k} - \vec{\mu})^t \Sigma^{-1}\right]^t + \frac{1}{2} \left[ \Sigma^{-1} (\vec{x_k} - \vec{\mu}) \right] = \Sigma^{-1} (\vec{x_k} - \vec{\mu}) $
Step 3: Equate to 0
$ \sum_{k=1}^{n} \Sigma^{-1} (\vec{x_k} - \vec{\mu}) = 0 $
$ \rightarrow \Sigma^{-1} \sum_{k=1}^{n} (\vec{x_k} - \vec{\mu}) = 0 $
$ \rightarrow \Sigma^{-1} \left[ \sum_{k=1}^{n} \vec{x_k} - n \vec{\mu}\right] = 0 $
$ \Longrightarrow \hat{\vec{\mu}} = \frac{1}{n} \sum_{k=1}^{n} \vec{x_k} $
This is the sample mean for a sample size n.
Examples of MLE: Exponential and Geometric Distributions
Examples of MLE: Binomial and Poisson Distributions
Advantages of MLE:
- Simple
- Converges
- Asymptotically unbiased (though biased for small N)
Bayesian Parameter Estimation
For a given class, let $ x $ be feature vector of the class and $ \theta $ be parameter of pdf of $ x $ to be estimated.
And let $ D= \{ x_1, x_2, \cdots, x_n \} $ , where $ x $ are training samples of the class
Note that $ \theta $ is random variable with probability density $ p(\theta) $
where
EXAMPLE: Bayesian Inference for Gaussian Mean
The univariate case. The variance is assumed to be known.
Here's a summary of results:
- Univariate Gaussian density $ p(x|\mu)\sim N(\mu,\sigma^{2}) $
- Prior density of the mean $ p(\mu)\sim N(\mu_{0},\sigma_{0}^{2}) $
- Posterior density of the mean $ p(\mu|D)\sim N(\mu_{n},\sigma_{n}^{2}) $
where
- $ \mu_{n}=\left(\frac{n\sigma_{0}^{2}}{n\sigma_{0}^{2}+\sigma^{2}}\right)\hat{\mu}_{n}+\frac{\sigma^{2}}{n\sigma_{0}^{2}+\sigma^{2}}\mu_{0} $
- $ \sigma_{n}^{2}=\frac{\sigma_{0}^{2}\sigma^{2}}{n\sigma_{0}^{2}+\sigma^{2}} $
- $ \hat{\mu}_{n}=\frac{1}{n}\sum_{k=1}^{n}x_{k} $
Finally, the class conditional density is given by $ p(x|D)\sim N(\mu_{n},\sigma^{2}+\sigma_{n}^{2}) $
The above formulas can be interpreted as: in making prediction for a single new observation, the variance of the estimate will have two components: 1) $ \sigma^{2} $ - the inherent variance within the distribution of x, i.e. the variance that would never be eliminated even with perfect information about the underlying distribution model; 2) $ \sigma_{n}^{2} $ - the variance introduced from the estimation of the mean vector "mu", this component can be eliminated given exact prior information or very large training set ( N goes to infinity);
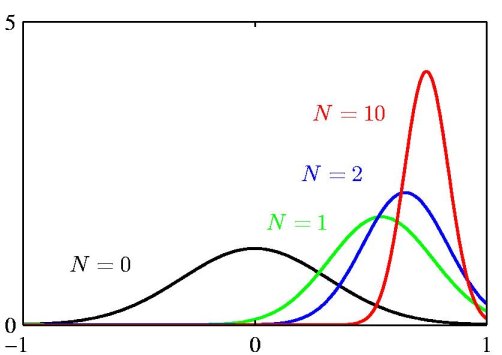
The above figure illustrates the Bayesian inference for the mean of a Gaussian distribution, for which the variance is assumed to be known. The curves show the prior distribution over 'mu' (the curve labeled N=0), which in this case is itself Gaussian, along with the posterior distributions for increasing number N of data points. The figure makes clear that as the number of data points increase, the posterior distribution peaks around the true value of the mean. This phenomenon is known as *Bayesian learning*.
For more information
- MLE: Maximum Likelihood Estimation
- BPE: Bayesian Parameter Estimation
- Comparison of MLE and Bayesian Parameter Estimation
- Parametric Estimators