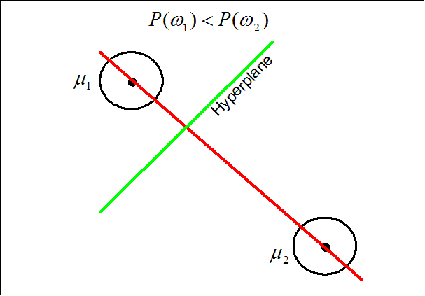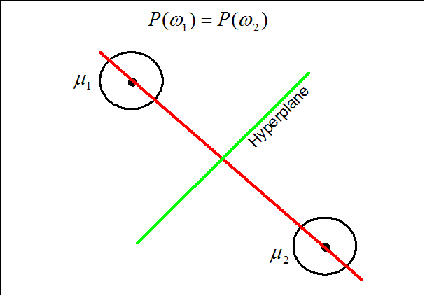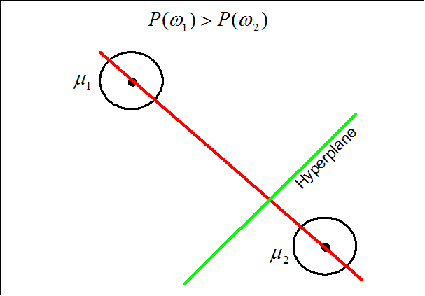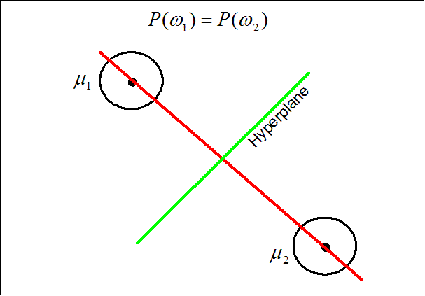| Line 1: | Line 1: | ||
| − | =Lecture notes for [[ECE662]], | + | =Lecture 6, [[ECE662]]: Decision Theory= |
| + | |||
| + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. | ||
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
---- | ---- | ||
| + | ---- | ||
| + | |||
=Lecture 6- Discriminant Functions= | =Lecture 6- Discriminant Functions= | ||
Latest revision as of 08:47, 17 January 2013
Lecture 6, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Lecture 6- Discriminant Functions
LECTURE THEME : - Discriminant Functions
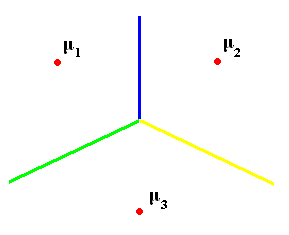
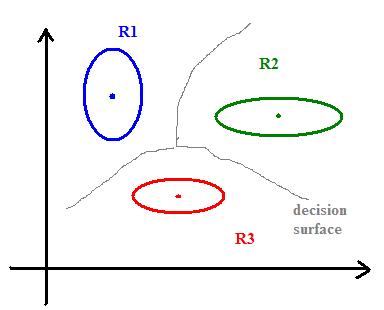
To separate several classes, we can draw the "skeleton" (Blum) of shape defined by mean vectors:
skeleton= set of points whose distance to the set $ \mu_1, ..., \mu_k $ is achieved by at least two different $ \mu_{i}'s $, i.e., we have $ dist(x,set)=min \{dist(x,\mu_i)\} $
and want $ \exists i_1 \neq i_2 $ such that $ dist(x,set)=dist(x,\mu_i1) =dist(x,\mu_i2) $
The skeleton is a decision boundary defining regions (chambers) $ R_i $ where we should decide $ w_i $.
What is the equation of these hyperplanes?
Recall the hyperplane equation: $ \{ \vec{x} | \vec{n} \cdot \vec{x} = const \} $
$ \vec{n} $ is a normal vector to the plane. Because if $ \vec{x_1} $ and $ \vec{x_2} $ are in this plane,
$ \Longrightarrow \vec{n} \cdot \vec{x_1} = const, \vec{n} \cdot \vec{x_2} = const $
$ \Longrightarrow \vec{n} \cdot (\vec{x_1} - \vec{x_2}) = const - const = 0 $
$ \therefore \vec{n} \bot ( \vec{x_1} - \vec{x_2}) $
Any linear structure can be written as
$ \sum_{i=1}^{n} c_i x_i + const = 0 $
Ex. of planes in $ \Re^{2} $
Example: for two classes $ w_1 $, $ w_2 $ hyperplane is defined by
$ \{ \vec{x} | g_1(\vec{x}) - g_2(\vec{x}) = 0 \} $
where, $ g_i(\vec{x})=-\frac{1}{2\sigma^2} \|\vec{x}-\mu_i\|_{L_2}^2+ \ln P(w_i) $
$ -\frac{1}{2\sigma^2} ((\vec{x}-\mu_i)^{\top}(\vec{x}-\mu_i)) + \ln P(w_i) $
$ -\frac{1}{2\sigma^2} (\vec{x}^{\top}\vec{x} - \vec{x}^{\top}\mu_i -\mu_i^{\top}\vec{x} + \mu_i^{\top}\mu_i ) + \ln P(w_i) $
but $ \vec{x}^{\top}\vec{\mu_i} $ is scalar $ \Longrightarrow \left( \vec{x}^{\top} \vec{\mu_i}\right)^{\top} = \vec{\mu_i}^{\top}\vec{x} = \vec{x}^{\top}\vec{\mu_i} $
$ \Longrightarrow g_i(\vec{x}) = -\frac{1}{2\sigma^2} \|\vec{x}\|^2 + \frac{1}{\sigma^2} \vec{x} \cdot \vec{\mu_i} - \frac{\mu_i^{\top}\mu_i}{2\sigma^2} + \ln P(w_i) $
First term is independent of $ i $, therefore we can remove first term from $ g_i\left( \vec{x}\right) $
$ \Longrightarrow g_i(\vec{x}) = \frac{1}{\sigma^2} \vec{x} \cdot \vec{\mu_i} - \frac{\vec{\mu_i} \cdot \vec{\mu_i}}{2 \sigma^2} + \ln P(w_i) $
which is a degree one polynomial in $ \vec{x} $.
A classifier that uses a linear discriminant function is called "linear machine".
The hyperplane between two classes is defined by
$ g_1(\vec{x}) - g_2(\vec{x}) = 0 $
$ \Leftrightarrow \frac{1}{\sigma^2} \vec{x}^{\top}\mu_1 - \frac{\mu_1^{\top}\mu_1}{2\sigma^2} + \ln P(w_1) $
$ - \frac{1}{\sigma^2} \vec{x}^{\top}\mu_2 + \frac{\mu_2^{\top}\mu_2}{2\sigma^2} - \ln P(w_2) = 0 $
$ \Leftrightarrow \frac{1}{\sigma^2} \vec{x} \cdot (\vec{\mu_1} - \vec{\mu_2}) =\frac{ \|\vec{\mu_1} \|^2}{2\sigma^2} - \frac{ \|\vec{\mu_2} \|^2}{2\sigma^2} + \ln P(w_2) -\ln P(w_1) $
Case 1: When $ P(w_1)=P(w_2) $
The hyperplane (black line) in this case goes through the middle line of the vector (gray line).
Case 2: $ \Sigma_i = \Sigma $ for all i's:
Recall: we can take $ g_i(\vec{x}) = -\frac{1}{2}\left( \vec{x}-\vec{\mu_i} \right)^{\top} \Sigma^{-1}\left(\vec{x}-\vec{\mu_i}\right) - \frac{n}{2}\ln 2\pi - \frac{1}{2} \ln |\Sigma| + \ln P(w_i) $
but $ \Sigma_i = \Sigma, - \frac{1}{2} \ln{2\pi} $ are independent of $ i $
Therefore, we remove these terms from $ g_i(\vec{x}) $, then new $ g_i(\vec{x}) $ will look like
$ \Longrightarrow g_i\left( \vec{x} \right) = - \frac{1}{2} \left( \vec{x} - \vec{\mu_i} \right)^{\top} \Sigma^{-1} \left( \vec{x} - \vec{\mu_i} \right) + \ln{P(w_i)} $
So, if all $ P\left( w_i \right) $'s are the same, assign $ \vec{x} $ to the class with the "nearest" mean.
Rewriting $ g_i(\vec{x}) $,
$ g_i(\vec{x}) = - \frac{1}{2} ( \vec{x}^{\top} \Sigma^{-1}\vec{x} - 2 \vec{\mu_i}^{\top} \Sigma^{-1}\vec{x} + \vec{\mu_i}^{\top}\Sigma^{-1}\vec{\mu_i}) + \ln{P(w_i)} $
Here we know that $ \vec{x}^{\top} \Sigma^{-1}\vec{x} $ is independent of $ i $, therefore we can remove this term from $ g_i(\vec{x}) $
$ \Longrightarrow g_i(\vec{x}) = \vec{\mu_i}^{\top} \Sigma^{-1}\vec{x} - \frac{1}{2} \vec{\mu_i}^{\top}\Sigma^{-1}\vec{\mu_i} + \ln{P(w_i)} $
Again this is a linear function of $ \vec{x} $
The equation of the hyperplane: $ (\vec{\mu_1}-\vec{\mu_2})^{\top}\Sigma^{-1}\vec{x} = \frac{1}{2} \vec{\mu_2}^{\top}\Sigma^{-1}\vec{\mu_2} - \frac{1}{2}\vec{\mu_1}^{\top}\Sigma^{-1}\vec{\mu_1} + \ln P(w_1) - \ln P(w_2) $
In sum, whatever the covariance structures are, as long as they are the same for all classes, the final discriminant functions would be linear (square terms dropped).
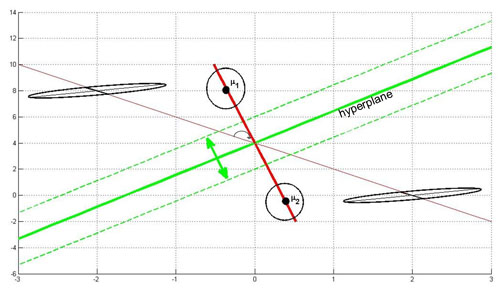
Below, you see an illustration of this case. If you have ellipses that have the same length and direction of the principal axis, you can modify them simultaneously to use Case 1.
The hyperplane (green line) is perpendicular to the red line conecting the two means. It moves along the red line depending on the value of $ P(w_1) $ and $ P(w_2) $. If $ P(w_1)=P(w_2) $ the hyperplane is located on the middle of the distance between the means.
Here's an animated version of the above figure:
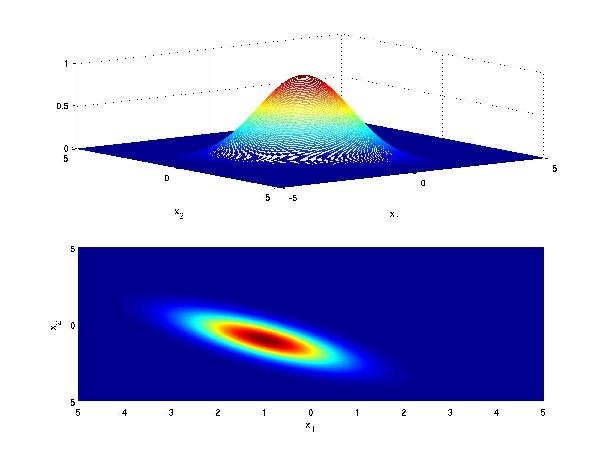
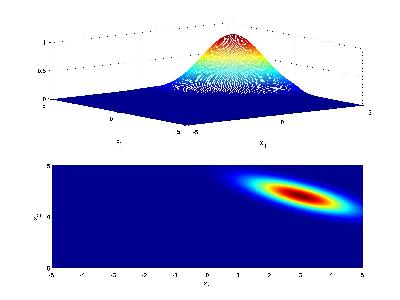
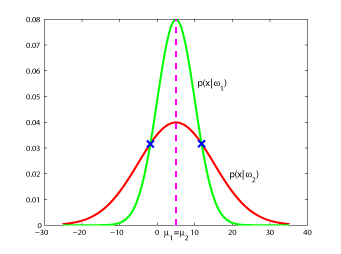
Another visualization for Case 2 is as follows: Consider class 1 which provides a multivariate Gaussian density on a 2D feature vector, when conditioned on that class.
Now consider class 2 with a similar Gaussian conditional density, but with different mean
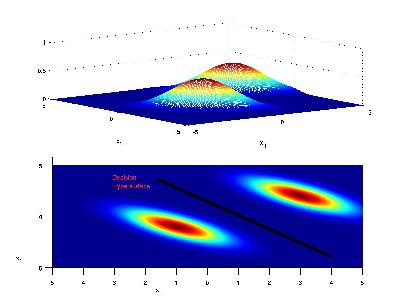
If the priors for each class are the same (i.e. 0.5), we have that the decision hypersurface cuts directly between the two means, with a direction parallel to the eliptical shape of the modes of the Gaussian densities shaped by their (identical) covariance matrices.
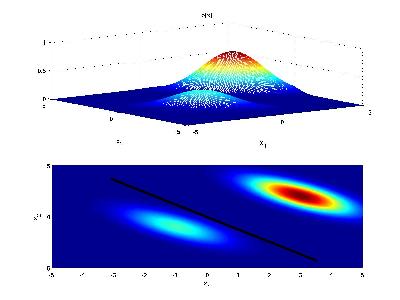
Now if the priors for each class are unequal, we have that the decision hypersurface cuts between the two means with a direction as before, but now will be located further from the more likely class. This biases the estimator in favor of the more likely class.
A video to visualize the decision hypersurface with changes to the Gaussian parameters is shown on the [Bayes Decision Rule] page.
Case 3: When $ \Sigma_i^{-1} $ is arbitrary
We can take
$ g_i(\vec{x}) = - \frac{1}{2} ( \vec{x} - \vec{\mu_i})^{\top}\Sigma_i^{-1}(\vec{x}-\vec{\mu_i})-\frac{1}{2} \ln \|\Sigma_i\|+ \ln P(w_i) $
the decision surface between $ w_1 $ and $ w_2 $:
is a degree 2 polynom in $ \vec{x} $
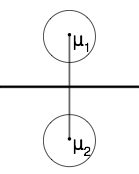
Note: decision boundaries must not be connected if $ P(w_1)=P(w_2) $ decision boundary has two disconnected points.
Class =w1, when -5<x<15
Class=w2, when x<-5 or x>15
For difference cases and their figures, refer to page 42 and 43 of DHS.