| (11 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 3, [[ECE662]]: Decision Theory= |
| + | |||
| + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. | ||
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| − | |||
LECTURE THEME : | LECTURE THEME : | ||
| Line 18: | Line 50: | ||
To find building blocks "g" or hypersurfaces of a classifier there are two approaches: | To find building blocks "g" or hypersurfaces of a classifier there are two approaches: | ||
| − | + | # Supervised Learning: Somebody provides a category label in a training set. This collection of examples is used to infer the rules to categorize other examples. | |
| − | + | # Unsupervised Learning: Very related to "Clustering", or the "Discovery of groupings". These groupings become the unknown classes that we want to discover in the measurements. Nobody places labels in the training set. In many cases Supervised methods are applied within Unsupervised method to separate known classes within clusters. | |
| − | * | + | ==== See Also ==== |
| + | * Zoubin Ghahramani's tutorial on Supervised, Reinforcement and Unsupervised Learning http://www.inf.ed.ac.uk/teaching/courses/pmr/docs/ul.pdf | ||
| − | High Dimensional | + | ===High Dimensional Issues=== |
| + | The [[curse of dimensionality_Old Kiwi]] starts at d>17-23. There are no clusters or groupings of data points when d>17. In practice each point turns to be a cluster on its own and as a result this explodes into a high dimensional feature vectors which are impossible to handle in computation. | ||
| − | + | == Bayes rule == | |
Bayes rule addresses the predefined classes classification problem. | Bayes rule addresses the predefined classes classification problem. | ||
| Line 61: | Line 95: | ||
<math>p(x|w_1)P(w_1) \geq p(x|w_2)P(w_2), {\forall j}</math><br> | <math>p(x|w_1)P(w_1) \geq p(x|w_2)P(w_2), {\forall j}</math><br> | ||
<math>P(w_1) \geq P(w_2)</math> decision is based on the prior<br> | <math>P(w_1) \geq P(w_2)</math> decision is based on the prior<br> | ||
| + | ---- | ||
| + | [[ECE662:BoutinSpring08_Old_Kiwi|Back to ECE662, Spring 2008, Prof. Boutin]] | ||
| + | [[Category:Lecture Notes]] | ||
| + | [[Category:ECE662]] | ||
Latest revision as of 08:46, 17 January 2013
Contents
Lecture 3, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
LECTURE THEME :
Bayes classification
Topics:
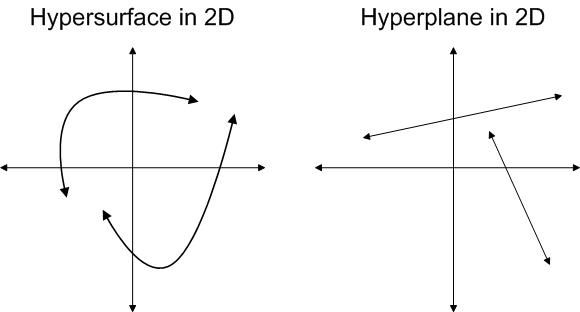
Clarification 1 - Difference between Hyperplane and Hypersurface: In simple terms, a hypersurface is any n-1 dimensional surface in n-dimensional space, while hyperplane is a flat hypersurface.
Clarification 2 - All classifiers are defined by hypersurfaces. - Consider a Nearest Neighbor classification problem: The classification of any query is decided by the label of its nearest neighbor. It may not be clear how this classifier can be defined by hypersurface. But we can define separating hypersurfaces which pass mid-way between points of different classes. In the extreme case, there can be a hypersurface for each data point enveloping all queries that will be classified with the label of that data point.
To find building blocks "g" or hypersurfaces of a classifier there are two approaches:
- Supervised Learning: Somebody provides a category label in a training set. This collection of examples is used to infer the rules to categorize other examples.
- Unsupervised Learning: Very related to "Clustering", or the "Discovery of groupings". These groupings become the unknown classes that we want to discover in the measurements. Nobody places labels in the training set. In many cases Supervised methods are applied within Unsupervised method to separate known classes within clusters.
See Also
- Zoubin Ghahramani's tutorial on Supervised, Reinforcement and Unsupervised Learning http://www.inf.ed.ac.uk/teaching/courses/pmr/docs/ul.pdf
High Dimensional Issues
The curse of dimensionality_Old Kiwi starts at d>17-23. There are no clusters or groupings of data points when d>17. In practice each point turns to be a cluster on its own and as a result this explodes into a high dimensional feature vectors which are impossible to handle in computation.
Bayes rule
Bayes rule addresses the predefined classes classification problem. Given value of X for an object, assign one of the k classes to the object
Bayes rule for discrete feature vector Bayes rule is to do the following: Given x=x, choose the most likely class $ E{\lbrace}w_1,...,w_k{\rbrace} $
$ w: E{\lbrace}w_1,...,w_k{\rbrace} $ ie. choose $ w_i $ such that the $ P(w_i|x) \geq P(w_j|x), {\forall}j $
$ posterior = \frac{(likelihood)(prior)}{(evidence)} $
$ posterior = P(w_i|x)= \frac{p(x|w_i)P(w_i)}{P(x)} $
Bayes rule: choose the class $ w_i $ that maximizes the $ p(x|w_i)P(w_i) $
Example: Given 2 class decision problems $ w_1 = $ women & $ w_2 $= men, $ L = hair length $ choose $ w_1 $, if $ P(w_1|L) \geq P(w_2|L) $ else choose $ w_2 $ or
choose $ w_1 $ if $ p(L|w_1)P(w_1)>p(L|w_2)P(w_2) $
else choose $ w_2 $
Minimum probability of error is the error made when $ w = w_2 $ and decided $ w_1 $
Special cases
If $ P(w_1) = P(w_2) $
$ p(x|w_1)P(w_1) \geq p(x|w_2)P(w_2), {\forall j} $
$ p(x|w_1) \geq p(x|w_2) $ decision is based on the likelihood
-If $ p(x|w_1)=p(x|w_2) $
$ p(x|w_1)P(w_1) \geq p(x|w_2)P(w_2), {\forall j} $
$ P(w_1) \geq P(w_2) $ decision is based on the prior