m (Translated some Zwiki tex references to mediawiki <math></math> blocks) |
|||
| (11 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[ECE662 | + | =Lecture 2, [[ECE662]]: Decision Theory= |
| − | [[ | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. |
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
== Lecture Theme == | == Lecture Theme == | ||
| Line 46: | Line 77: | ||
====Note==== | ====Note==== | ||
| − | If the cost function | + | If the cost function <math>c(x)</math> from '''Meaning 2''' is defined to be 1 for an error, and 0 otherwise, then <math>E[c(x)] = P[error]</math>, so that '''Meaning 1''' is a special case of '''Meaning 2'''. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
====Illustration==== | ====Illustration==== | ||
| Line 59: | Line 84: | ||
Use hairlength as the single feature. | Use hairlength as the single feature. | ||
| − | + | [[image:hairlength.jpg]] | |
Histogram represents the actual numbers. | Histogram represents the actual numbers. | ||
| − | Decision hypersurface: | + | Decision hypersurface: <math>l-6=0</math>. |
This is the best decision rule in the sense that it minimizes the probability of error. Can not do better than this for the scenario where only hairlength is used as the feature. | This is the best decision rule in the sense that it minimizes the probability of error. Can not do better than this for the scenario where only hairlength is used as the feature. | ||
| − | |||
| − | |||
| − | |||
====Remember==== | ====Remember==== | ||
| Line 76: | Line 98: | ||
===Work in low dimensionality as far as possible=== | ===Work in low dimensionality as far as possible=== | ||
| − | Why? This is typically explained as the [[curse of dimensionality_Old Kiwi]]. For more, this term can be googled. There is a nice | + | Why? This is typically explained as the [[curse of dimensionality_Old Kiwi]]. For more, this term can be googled. There is a nice [http://citeseer.ist.psu.edu/cache/papers/cs/25919/http:zSzzSzwww.informatik.uni-halle.dezSz~keimzSzPSzSzvldb2000.pdf/hinneburg00what.pdfciteseer| paper] in VLDB 2000 that discusses the notion of nearest-neighbors in high dimensional spaces. |
| − | Let | + | Let <math>x_{1},x_{2},\ldots,x_{N}</math> be features. Suppose we use a large number of features to come up with a decision hypersurface <math>g(x_{1},x_{2},\ldots,x_{N})=0</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Then g is the single feature we need. | Then g is the single feature we need. | ||
| Line 90: | Line 106: | ||
Previous: [[Lecture 1-Introduction_Old Kiwi]] | Previous: [[Lecture 1-Introduction_Old Kiwi]] | ||
Next: [[Lecture 3_Old Kiwi]] | Next: [[Lecture 3_Old Kiwi]] | ||
| + | |||
| + | [[Category:Lecture Notes]] | ||
Latest revision as of 08:45, 17 January 2013
Lecture 2, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Lecture Theme
Decision hypersurfaces
Actual Lecture
Making decisions is the art of drawing hypersurfaces.
Hypersurfaces_Old Kiwi discussed in this lecture
These Hypersurfaces_Old Kiwi are discussed in this lecture:
- Linear Separations
- Straight lines in 2D $ ax+by+c=0 $
- Planes in 3D $ ax+by+cx+d=0 $
- Hyperplanes in nD $ \sum a_i x_i = \textrm{constant} $
- Union of linear separations
- Tree-based separation
Combining Hypersurfaces
Main article: Combining Hypersurfaces_Old Kiwi
Hypersurfaces are combined by multiplication of the functions which define them, not by intersection.
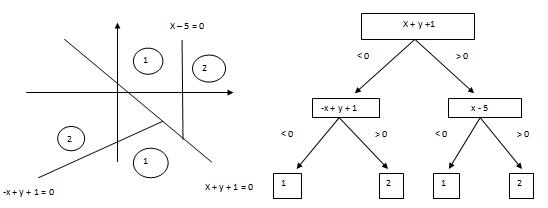
Tree Based Separation
By using union of hypersurfaces, classes can be separated by a tree based structure. Tree based separation is harder, and obtaining an optimum decision tree is another difficult problem in pattern recognition.
Example:
Question: What do we mean by good separation?
Question: What do we mean by good separation?
Meaning 1: One that will make few mistakes when used to classify actual data. In statistical language: small probability of error.
Meaning 2: One that will make mistakes that will not be too costly. In statistical language: small expected cost of errors.
Note
If the cost function $ c(x) $ from Meaning 2 is defined to be 1 for an error, and 0 otherwise, then $ E[c(x)] = P[error] $, so that Meaning 1 is a special case of Meaning 2.
Illustration
Take 50,000 people in an airport. We want to be able to distinguish men from women among these 50,000 people.
Use hairlength as the single feature.
Histogram represents the actual numbers.
Decision hypersurface: $ l-6=0 $. This is the best decision rule in the sense that it minimizes the probability of error. Can not do better than this for the scenario where only hairlength is used as the feature.
Remember
- Good features produce distinct bumps. That is try to choose features that have a natural grouping for a particular class. For example, hair-length is a good feature to separate men from women as more most men are likely to have short hair-length.
- Bad features (e.g. background color) produce overlapping bumps.
- In order to get a good decision algorithm, we need to have good features (and good separation too).
Work in low dimensionality as far as possible
Why? This is typically explained as the curse of dimensionality_Old Kiwi. For more, this term can be googled. There is a nice paper in VLDB 2000 that discusses the notion of nearest-neighbors in high dimensional spaces.
Let $ x_{1},x_{2},\ldots,x_{N} $ be features. Suppose we use a large number of features to come up with a decision hypersurface $ g(x_{1},x_{2},\ldots,x_{N})=0 $
Then g is the single feature we need.
Previous: Lecture 1-Introduction_Old Kiwi Next: Lecture 3_Old Kiwi