(→=) |
|||
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 13, [[ECE662]]: Decision Theory= |
| − | [ | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. |
| − | + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | |
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| − | |||
| − | |||
| − | |||
| − | + | [[Kernel Functions_Old Kiwi|Why kernel functions?]] | |
| − | =============== | + | == Kernel Functions == |
| + | Last class introduced kernel functions trick as a key to make SVM an effective tool for classifying linearly separable data. Here we see some examples of kernel functions, and the condition that determined if these functions correspond to dot product in some feature space. | ||
| + | |||
| + | Note that | ||
| + | <math> \varphi</math>can be a mapping as | ||
| + | <math>\varphi:\Re^k\rightarrow\mathbb{H} | ||
| + | </math> | ||
| + | |||
| + | where <math>\mathbb{H}</math> can be <math>\infty</math> dimensional. | ||
| + | |||
| + | Here is the example of a "Gaussian Kernel" with <math> \varphi</math> as <math>\infty</math> dimensional. | ||
| + | <math>k(\vec{x},\vec{x'})=e^{-\frac{||\vec{x}-\vec{x}||^2}{2\sigma^2}}</math>, <math>\sigma</math> parameter. | ||
| + | |||
| + | It is easier to work with <math>k(\vec{x},\vec{x'})</math> than with <math>\varphi(\vec{x})</math>. | ||
| + | |||
| + | |||
| + | In this example, computation of the dot product <math> \varphi(\vec{x}) \cdot \varphi(\vec{x'}) </math>requires infinite summation. Kernel function allows us to compute distance to hyperplane with same computational cost as training SVM in initial data space. | ||
| + | |||
| + | |||
| + | '''For which kernel does there exist a mapping to a higher dimensional space?''' | ||
| + | |||
| + | |||
| + | The answer lies in Mercer's Condition (Covrant and Hilbert in '53; Vapnik in '95) | ||
| + | |||
| + | |||
| + | Given a kernel <math>K:\Re ^k \times \Re ^k \rightarrow \Re</math>, there exists a <math>\varphi | ||
| + | </math> and an expansion | ||
| + | |||
| + | <math> k(\vec{x},\vec{x'})=\sum_{i}\varphi(\vec{x})_{i}\varphi(\vec{x'})_{i}</math>, where i could range in infinite space | ||
| + | |||
| + | <math> \Longleftrightarrow \forall g(\vec{x}) </math> | ||
| + | <math>\int [g(\vec{x})]^{2}d\vec{x}<\infty</math> | ||
| + | |||
| + | <math>\int\int k(\vec{x},\vec{x'})g(\vec{x})g(\vec{x'})d\vec{x}d\vec{x'}\geq 0</math> | ||
| + | |||
| + | This condition is satisfied for | ||
| + | <math>k(\vec{x},\vec{x'})=||\vec{x}-\vec{x'}||^p</math> | ||
| + | for any <math>p\in \mathbb{N}</math> | ||
| + | |||
| + | |||
| + | In this case, <math> \varphi</math> is a polynomial mapping, homogeneous with degree p in each component. | ||
| + | |||
| + | e.g. <math>\varphi(\vec{x})=(\varphi_{r_1r_2\ldots r_{d_L}}(\vec{x})) | ||
| + | </math> where <math>\varphi_{r_1r_2\ldots r_{d_L}}(\vec{x})=(\sqrt{\frac{p!}{r_{1}!\ldots r_{d_L}!}}){x_1}^{r_1}\ldots {x_{d_L}}^{r_{d_L}}</math> | ||
| + | |||
| + | and | ||
| + | |||
| + | <math>\sum_{i=1}^{d_L}r_i=p</math>, <math>r_i\geq 0</math> | ||
| + | |||
| + | '''Example''' : <math>p(x,y)=7x^2-14y^2+3xy</math> | ||
| + | |||
| + | |||
| + | To visualize the separation surface we need to find x and y such that: | ||
| + | |||
| + | <math> p(x,y)=0</math> | ||
| + | |||
| + | To solve such equation, we could take a segment of y and divide it on intervals. On each interval we fix a value of y and solve the quadratic function for x. Then, we connect the resulting points to see the surface. This example is illustrated on the figure below this paragraph. | ||
| + | |||
| + | .. image:: mortiz_lec13.gif | ||
| + | :align: center | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Artificial Neural Networks == | ||
What is a Neural Network? | What is a Neural Network? | ||
------------------------------------------ | ------------------------------------------ | ||
| − | An [Artificial Neural Network] is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information. The key element of this paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning in biological systems involves adjustments to the synaptic connections that exist between the neurones. This is true of ANNs as well. | + | An [Artificial Neural Network] is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information. The key element of this paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning in biological systems involves adjustments to the synaptic connections that exist between the neurones. This is true of ANNs as well. |
General Properties: | General Properties: | ||
| Line 23: | Line 113: | ||
Other advantages include: | Other advantages include: | ||
| − | + | 1. Adaptive learning: An ability to learn how to do tasks based on the data given for training or initial experience. | |
| − | + | 2. Self-Organization: An ANN can create its own organization or representation of the information it receives during learning time. | |
Neural networks are a family of function approximation techniques, when the function is approximated, | Neural networks are a family of function approximation techniques, when the function is approximated, | ||
| − | + | <math>f:x \rightarrow z</math> (1) | |
| − | is modeled as a composition of simple functions | + | is modeled as a composition of simple functions <math>f_i's</math> |
| − | + | <math>f=f_n\bullet f_{n-1}\cdot\cdot\cdot f_1</math> (2) | |
The composition model is represented by a network | The composition model is represented by a network | ||
| − | Several | + | Several <math>f_i's</math> are taken to be linear functions |
The parameters of the linear functions are optimized to best fit the data | The parameters of the linear functions are optimized to best fit the data | ||
| Line 42: | Line 132: | ||
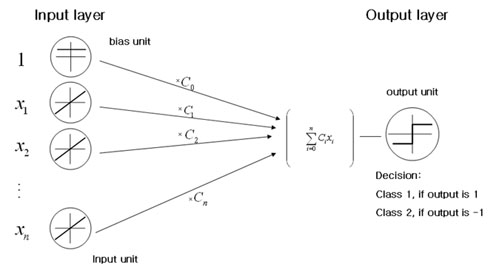
Example) [Linear Discriminant Functions] can be seen as a two layer Neural Network(NN) | Example) [Linear Discriminant Functions] can be seen as a two layer Neural Network(NN) | ||
| − | recall | + | recall <math>g(\vec{x})=\vec{c}\cdot (1,\vec{x})</math> (3) |
| − | + | <math>g(\vec{x}) > 0 \Rightarrow class 1 , < 0 \Rightarrow class 2</math> (4) | |
| − | write | + | write |
| − | + | <math>\vec{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{pmatrix}</math> (5) | |
| − | + | [[Image:NN_2layer_2_Old Kiwi.jpg]] | |
| − | + | ||
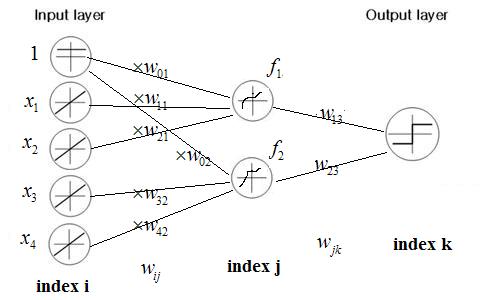
Example of three layer NN | Example of three layer NN | ||
| − | + | [[Image:NN_3layer_Old Kiwi.jpg]] | |
Common types of function fi's | Common types of function fi's | ||
| − | linear: | + | linear: <math>f(\vec x)=\vec c^T\vec x+c_0</math> (6) |
| − | + | logistic: <math>f(x)=\frac{e^x}{1+e^x}</math> (7) | |
| − | + | ||
| − | + | threshold: <math>f(x)=1,x>0;f(x)=0,else</math> (8) | |
| − | + | hyperbolic tangent: <math>f(x)=\frac{e^x-1}{e^x+1}</math> (9) | |
| − | + | ||
| − | + | sign function: <math>f(x)=1,x>0;f(x)=-1,else</math> (10) | |
| − | + | any continuous <math>g(\vec x):[0,1]*[0,1]*...*[0,1]\rightarrow\Re</math> (11) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | any continuous | + | |
| − | + | ||
| − | + | ||
| − | + | ||
can be written as : | can be written as : | ||
| − | + | <math>g(\vec{x})=\sum _{j=1}^{2n+1} G_j(\sum _{i} \psi _{ij} (x_i))</math> (12) | |
| − | + | ||
| − | + | ||
| − | + | ||
Training Neural Networks - "Back-Propagation Algorithm" | Training Neural Networks - "Back-Propagation Algorithm" | ||
--------------------------------------------------------- | --------------------------------------------------------- | ||
| − | + | First define a cost function to measure the error of the neural network with weights <math>\vec{w}</math>, say we have training input values <math>\vec{x_k}</math> => output <math>z_k</math>, but desire output <math>t_k</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | First define a cost function to measure the error of the neural network with weights | + | |
This cost function can be written as below | This cost function can be written as below | ||
| − | + | <math>J(\vec{w}) = \frac{1}{2} \sum_{k} (t_k - z_k)^2 = \frac{1}{2} \mid \vec{t} - \vec{k} \mid ^2</math> (13) | |
| − | + | ||
| − | + | ||
| − | + | ||
Then, we can optimize this cost function using gradient descent method | Then, we can optimize this cost function using gradient descent method | ||
| − | + | new <math>\vec{w}=</math> old <math>\vec{w}+ \Delta \vec{w}</math> (14) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math>\rightarrow \vec{w}(k+1) = \vec{w}(k) - \eta(k) \left( \frac{\partial J}{\partial w_1}, \frac{\partial J}{\partial w_2}, \cdots , \frac{\partial J}{\partial w_{last}} \right)</math> (15) | |
| − | |||
| − | |||
| + | Previous: [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi]]; Next: [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen_Window)_Old Kiwi]] | ||
| − | + | [[Category:Lecture Notes]] | |
Latest revision as of 08:51, 17 January 2013
Lecture 13, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Kernel Functions
Last class introduced kernel functions trick as a key to make SVM an effective tool for classifying linearly separable data. Here we see some examples of kernel functions, and the condition that determined if these functions correspond to dot product in some feature space.
Note that $ \varphi $can be a mapping as $ \varphi:\Re^k\rightarrow\mathbb{H} $
where $ \mathbb{H} $ can be $ \infty $ dimensional.
Here is the example of a "Gaussian Kernel" with $ \varphi $ as $ \infty $ dimensional. $ k(\vec{x},\vec{x'})=e^{-\frac{||\vec{x}-\vec{x}||^2}{2\sigma^2}} $, $ \sigma $ parameter.
It is easier to work with $ k(\vec{x},\vec{x'}) $ than with $ \varphi(\vec{x}) $.
In this example, computation of the dot product $ \varphi(\vec{x}) \cdot \varphi(\vec{x'}) $requires infinite summation. Kernel function allows us to compute distance to hyperplane with same computational cost as training SVM in initial data space.
For which kernel does there exist a mapping to a higher dimensional space?
The answer lies in Mercer's Condition (Covrant and Hilbert in '53; Vapnik in '95)
Given a kernel $ K:\Re ^k \times \Re ^k \rightarrow \Re $, there exists a $ \varphi $ and an expansion
$ k(\vec{x},\vec{x'})=\sum_{i}\varphi(\vec{x})_{i}\varphi(\vec{x'})_{i} $, where i could range in infinite space
$ \Longleftrightarrow \forall g(\vec{x}) $ $ \int [g(\vec{x})]^{2}d\vec{x}<\infty $
$ \int\int k(\vec{x},\vec{x'})g(\vec{x})g(\vec{x'})d\vec{x}d\vec{x'}\geq 0 $
This condition is satisfied for $ k(\vec{x},\vec{x'})=||\vec{x}-\vec{x'}||^p $ for any $ p\in \mathbb{N} $
In this case, $ \varphi $ is a polynomial mapping, homogeneous with degree p in each component.
e.g. $ \varphi(\vec{x})=(\varphi_{r_1r_2\ldots r_{d_L}}(\vec{x})) $ where $ \varphi_{r_1r_2\ldots r_{d_L}}(\vec{x})=(\sqrt{\frac{p!}{r_{1}!\ldots r_{d_L}!}}){x_1}^{r_1}\ldots {x_{d_L}}^{r_{d_L}} $
and
$ \sum_{i=1}^{d_L}r_i=p $, $ r_i\geq 0 $
Example : $ p(x,y)=7x^2-14y^2+3xy $
To visualize the separation surface we need to find x and y such that:
$ p(x,y)=0 $
To solve such equation, we could take a segment of y and divide it on intervals. On each interval we fix a value of y and solve the quadratic function for x. Then, we connect the resulting points to see the surface. This example is illustrated on the figure below this paragraph.
.. image:: mortiz_lec13.gif
- align: center
Artificial Neural Networks
What is a Neural Network?
An [Artificial Neural Network] is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information. The key element of this paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning in biological systems involves adjustments to the synaptic connections that exist between the neurones. This is true of ANNs as well.
General Properties:
Neural networks, with their remarkable ability to derive meaning from complicated or imprecise data, can be used to extract patterns and detect trends that are too complex to be noticed by either humans or other computer techniques. A trained neural network can be thought of as an "expert" in the category of information it has been given to analyze. This expert can then be used to provide projections given new situations of interest and answer "what if" questions. Other advantages include:
1. Adaptive learning: An ability to learn how to do tasks based on the data given for training or initial experience. 2. Self-Organization: An ANN can create its own organization or representation of the information it receives during learning time.
Neural networks are a family of function approximation techniques, when the function is approximated,
$ f:x \rightarrow z $ (1)
is modeled as a composition of simple functions $ f_i's $
$ f=f_n\bullet f_{n-1}\cdot\cdot\cdot f_1 $ (2)
The composition model is represented by a network
Several $ f_i's $ are taken to be linear functions
The parameters of the linear functions are optimized to best fit the data
Example) [Linear Discriminant Functions] can be seen as a two layer Neural Network(NN)
recall $ g(\vec{x})=\vec{c}\cdot (1,\vec{x}) $ (3)
$ g(\vec{x}) > 0 \Rightarrow class 1 , < 0 \Rightarrow class 2 $ (4)
write
$ \vec{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{pmatrix} $ (5)
Example of three layer NN
Common types of function fi's
linear: $ f(\vec x)=\vec c^T\vec x+c_0 $ (6)
logistic: $ f(x)=\frac{e^x}{1+e^x} $ (7)
threshold: $ f(x)=1,x>0;f(x)=0,else $ (8)
hyperbolic tangent: $ f(x)=\frac{e^x-1}{e^x+1} $ (9)
sign function: $ f(x)=1,x>0;f(x)=-1,else $ (10)
any continuous $ g(\vec x):[0,1]*[0,1]*...*[0,1]\rightarrow\Re $ (11)
can be written as :
$ g(\vec{x})=\sum _{j=1}^{2n+1} G_j(\sum _{i} \psi _{ij} (x_i)) $ (12)
Training Neural Networks - "Back-Propagation Algorithm"
First define a cost function to measure the error of the neural network with weights $ \vec{w} $, say we have training input values $ \vec{x_k} $ => output $ z_k $, but desire output $ t_k $.
This cost function can be written as below
$ J(\vec{w}) = \frac{1}{2} \sum_{k} (t_k - z_k)^2 = \frac{1}{2} \mid \vec{t} - \vec{k} \mid ^2 $ (13)
Then, we can optimize this cost function using gradient descent method
new $ \vec{w}= $ old $ \vec{w}+ \Delta \vec{w} $ (14)
$ \rightarrow \vec{w}(k+1) = \vec{w}(k) - \eta(k) \left( \frac{\partial J}{\partial w_1}, \frac{\partial J}{\partial w_2}, \cdots , \frac{\partial J}{\partial w_{last}} \right) $ (15)
Previous: Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi; Next: Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen_Window)_Old Kiwi