| (25 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 11, [[ECE662]]: Decision Theory= |
| − | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. | |
| − | == | + | |
| − | Main article: [Derivation of Fisher's Linear | + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], |
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
| + | |||
| + | == Derivation of Fischer's Linear Discriminant == | ||
| + | |||
| + | Main article: [[Derivation of Fisher's Linear Discriminant_Old Kiwi]] | ||
The derivation was completed in this lecture. | The derivation was completed in this lecture. | ||
| − | Recall from last lecture | + | == Recall from last lecture == |
| − | + | ||
Last time, we considered | Last time, we considered | ||
| Line 15: | Line 47: | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
which is explicit function of <math>\vec{w}</math> | which is explicit function of <math>\vec{w}</math> | ||
| − | |||
| − | |||
| − | |||
One can do this because numerator of <math>J(\vec{w})</math> can be written as | One can do this because numerator of <math>J(\vec{w})</math> can be written as | ||
| Line 31: | Line 56: | ||
<math>\rightarrow S_B = (m_1 - m_2) (m_1^t - m_2^t)</math> | <math>\rightarrow S_B = (m_1 - m_2) (m_1^t - m_2^t)</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
In a same way, denominator can be written as | In a same way, denominator can be written as | ||
| Line 50: | Line 66: | ||
| − | Fisher Linear Discriminant | + | == Fisher Linear Discriminant == |
| − | + | ||
| + | It is a known result that J is maximum at <math>\omega_0</math> such that <math>S_B\omega_0=\lambda S_W\omega_0</math>. This is the "Generalized eigenvalue problem. | ||
| − | + | Note that if <math>|S_W|\neq 0</math>, then <math>{S_W}^{-1}S_B\omega_0=\lambda\omega_0</math>. It can be written as the "Standard eigenvalue problem". The only difficulty (which is a big difficulty when the feature space dimension is large) is that matrix inversion is very unstable. | |
| − | + | ||
| − | |||
| − | |||
| + | Observe that <math>S_B\omega_0=(\vec{m_1}-\vec{m_2})(\vec{m_1}-\vec{m_2})^T\omega_0=cst.(\vec{m_1}-\vec{m_2})</math>. Therefore the standard eigenvalue problem as presented above becomes <math>{S_W}^{-1}cst.(\vec{m_1}-\vec{m_2})=\lambda\omega_0</math>. From this equation, value of <math>\omega_0</math> can easily be obtained, as <math>\omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2})</math> or any constant multiple of this. Note that magnitude of <math>\omega_0</math> is not important, the direction it represents is important. | ||
| − | + | == Fischer's Linear Discriminant in Projected Coordinates == | |
| − | + | ||
| + | ===Claim=== | ||
| − | + | <math>\vec{c}=\omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2}) | |
| − | + | </math> | |
| − | + | is the solution to <math>\mathbf{Y}\vec{c}=\vec{b}</math> with <math>\vec{b}=(d/d_1, \cdots, <d_1 times>, d/(d-d_1), \cdots, <(d-d_1) times>)^T</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Here is an animation of the 1D example given in class on projections | Here is an animation of the 1D example given in class on projections | ||
| − | + | [[Image:lecture11-1_Old Kiwi.gif]] | |
| − | + | ===Explanation=== | |
| − | + | ||
| − | + | starts with <math>\vec{\omega} \cdot y_i + \omega_0 > 0</math> for class 1 and <math>\vec{\omega} \cdot y_i + \omega_0 < 0</math> for class 2 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
the data points are then projected onto an axis at 1 which results in | the data points are then projected onto an axis at 1 which results in | ||
| − | + | <math>\vec{\omega} \cdot y_i > 0</math> for class 1 and <math>\vec{\omega} \cdot y_i < 0</math> for class 2 | |
one class is then projected onto an axis at -1 which results in | one class is then projected onto an axis at -1 which results in | ||
| − | + | <math>\vec{\omega} \cdot y_i > 0</math> for all <math>y_i</math> | |
| + | == Support Vector Machines (SVM) == | ||
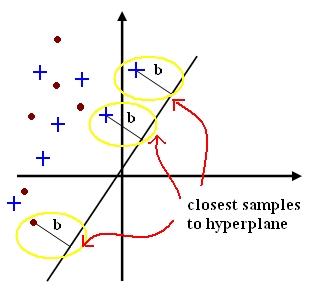
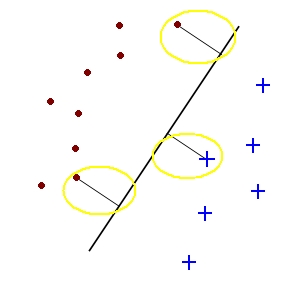
| − | + | A support vector for a hyperplane <math>\vec{c}</math> with margin <math>b_i \geq b</math> is a sample <math>y_{io}</math> such that <math>c\cdot{y_{io}} = b</math>. | |
| − | + | [[Image:lec11_sv_pic1_Old Kiwi.jpg]] | |
| − | + | [[Image:lec11_sv_pic2_Old Kiwi.jpg]] | |
| − | + | ||
Support Vector Machines are a two step process: | Support Vector Machines are a two step process: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 1) Preprocessing - X1,...,Xd features in kth dimensional real space is mapped to features in n dimensional real space where n>>k. | ||
| − | + | 2) Linear Classifier - separates classes in n dimensional real space via hyperplane. | |
| − | + | - Support Vectors - for finding the hyperplane with the biggest margins. | |
| − | + | - Kernel - to simplify computation (This is key for real world applications) | |
| + | ---- | ||
| − | [ | + | [[ECE662:BoutinSpring08_Old_Kiwi|Back to ECE662, Spring 2008, Prof. Boutin]] |
| + | [[Category:Lecture Notes]] | ||
Latest revision as of 08:49, 17 January 2013
Contents
Lecture 11, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
Derivation of Fischer's Linear Discriminant
Main article: Derivation of Fisher's Linear Discriminant_Old Kiwi
The derivation was completed in this lecture.
Recall from last lecture
Last time, we considered
$ J(\vec{w}) = \frac{\vec{w}^t S_B \vec{w}}{\vec{w}^t S_W \vec{w}} $
which is explicit function of $ \vec{w} $
One can do this because numerator of $ J(\vec{w}) $ can be written as
$ \mid \tilde m_1 - \tilde m_2 \mid^2 = \mid w \cdot (m_1 - m_2) \mid^2 = w^t (m_1 - m_2) (m_1^t - m_2^t) w $
$ \rightarrow S_B = (m_1 - m_2) (m_1^t - m_2^t) $
In a same way, denominator can be written as
$ \tilde s_1^2 + \tilde s_2^2 = \sum_{y_i \in class \ i} (w \cdot y_i - \tilde m_1)^2 = \sum w^t (y_i - m_i)(y_i^t - m_i^t) w $
$ = w^t \left[ \sum (y_i - m_i)(y_i^t - m_i^t) \right] w $
$ \rightarrow S_W = \sum_{y_i \in class \ i} (y_i - m_i)(y_i^t - m_i^t) $
Fisher Linear Discriminant
It is a known result that J is maximum at $ \omega_0 $ such that $ S_B\omega_0=\lambda S_W\omega_0 $. This is the "Generalized eigenvalue problem.
Note that if $ |S_W|\neq 0 $, then $ {S_W}^{-1}S_B\omega_0=\lambda\omega_0 $. It can be written as the "Standard eigenvalue problem". The only difficulty (which is a big difficulty when the feature space dimension is large) is that matrix inversion is very unstable.
Observe that $ S_B\omega_0=(\vec{m_1}-\vec{m_2})(\vec{m_1}-\vec{m_2})^T\omega_0=cst.(\vec{m_1}-\vec{m_2}) $. Therefore the standard eigenvalue problem as presented above becomes $ {S_W}^{-1}cst.(\vec{m_1}-\vec{m_2})=\lambda\omega_0 $. From this equation, value of $ \omega_0 $ can easily be obtained, as $ \omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2}) $ or any constant multiple of this. Note that magnitude of $ \omega_0 $ is not important, the direction it represents is important.
Fischer's Linear Discriminant in Projected Coordinates
Claim
$ \vec{c}=\omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2}) $
is the solution to $ \mathbf{Y}\vec{c}=\vec{b} $ with $ \vec{b}=(d/d_1, \cdots, <d_1 times>, d/(d-d_1), \cdots, <(d-d_1) times>)^T $
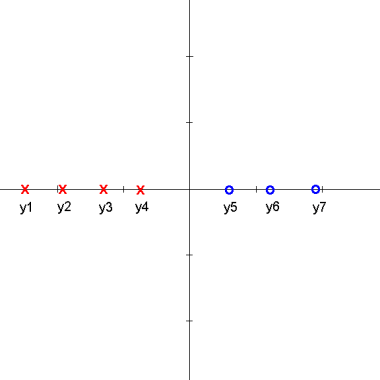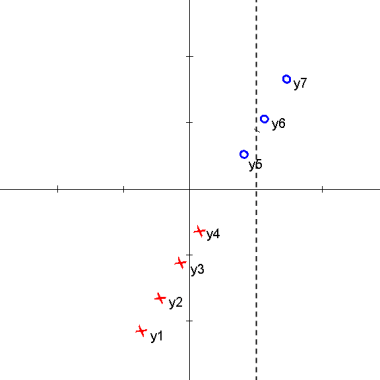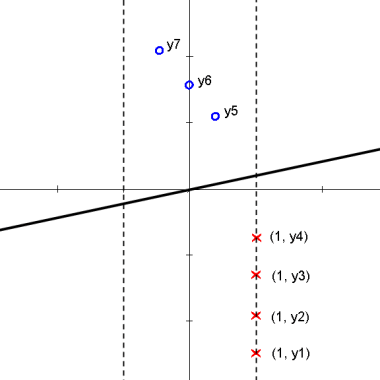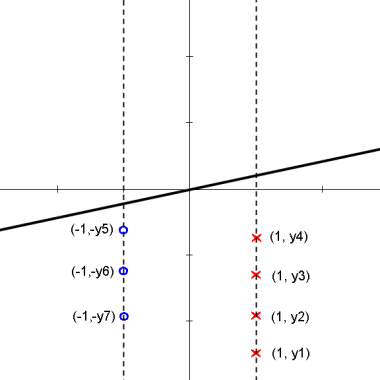
Here is an animation of the 1D example given in class on projections
Explanation
starts with $ \vec{\omega} \cdot y_i + \omega_0 > 0 $ for class 1 and $ \vec{\omega} \cdot y_i + \omega_0 < 0 $ for class 2
the data points are then projected onto an axis at 1 which results in
$ \vec{\omega} \cdot y_i > 0 $ for class 1 and $ \vec{\omega} \cdot y_i < 0 $ for class 2
one class is then projected onto an axis at -1 which results in
$ \vec{\omega} \cdot y_i > 0 $ for all $ y_i $
Support Vector Machines (SVM)
A support vector for a hyperplane $ \vec{c} $ with margin $ b_i \geq b $ is a sample $ y_{io} $ such that $ c\cdot{y_{io}} = b $.
Support Vector Machines are a two step process:
1) Preprocessing - X1,...,Xd features in kth dimensional real space is mapped to features in n dimensional real space where n>>k.
2) Linear Classifier - separates classes in n dimensional real space via hyperplane. - Support Vectors - for finding the hyperplane with the biggest margins. - Kernel - to simplify computation (This is key for real world applications)