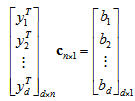| (4 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | =Lecture 10, [[ECE662]]: Decision Theory= |
| − | [ | + | Lecture notes for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662 Spring 2008]], Prof. [[user:mboutin|Boutin]]. |
| + | |||
| + | Other lectures: [[Lecture 1 - Introduction_Old Kiwi|1]], | ||
| + | [[Lecture 2 - Decision Hypersurfaces_Old Kiwi|2]], | ||
| + | [[Lecture 3 - Bayes classification_Old Kiwi|3]], | ||
| + | [[Lecture 4 - Bayes Classification_Old Kiwi|4]], | ||
| + | [[Lecture 5 - Discriminant Functions_Old Kiwi|5]], | ||
| + | [[Lecture 6 - Discriminant Functions_Old Kiwi|6]], | ||
| + | [[Lecture 7 - MLE and BPE_Old Kiwi|7]], | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_Old Kiwi|8]], | ||
| + | [[Lecture 9 - Linear Discriminant Functions_Old Kiwi|9]], | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_Old Kiwi|10]], | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_Old Kiwi|11]], | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_Old Kiwi|12]], | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_Old Kiwi|13]], | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_Old Kiwi|14]], | ||
| + | [[Lecture 15 - Parzen Window Method_Old Kiwi|15]], | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_Old Kiwi|16]], | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_Old Kiwi|17]], | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_Old Kiwi|18]], | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_Old Kiwi|19]], | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_Old Kiwi|20]], | ||
| + | [[Lecture 21 - Decision Trees(Continued)_Old Kiwi|21]], | ||
| + | [[Lecture 22 - Decision Trees and Clustering_Old Kiwi|22]], | ||
| + | [[Lecture 23 - Spanning Trees_Old Kiwi|23]], | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_Old Kiwi|24]], | ||
| + | [[Lecture 25 - Clustering Algorithms_Old Kiwi|25]], | ||
| + | [[Lecture 26 - Statistical Clustering Methods_Old Kiwi|26]], | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_Old Kiwi|27]], | ||
| + | [[Lecture 28 - Final lecture_Old Kiwi|28]], | ||
| + | ---- | ||
| + | ---- | ||
The perceptron algorithm maps an input to a single binary output value. For a proof of the Perceptron convergence theorem, see [PerceptronConvergenceTheorem] | The perceptron algorithm maps an input to a single binary output value. For a proof of the Perceptron convergence theorem, see [PerceptronConvergenceTheorem] | ||
First introduced in [Lecture 9]. The gradient descent algorithm used is discussed in [Lecture 10]. | First introduced in [Lecture 9]. The gradient descent algorithm used is discussed in [Lecture 10]. | ||
| + | |||
| + | __TOC__ | ||
== Gradient Descent == | == Gradient Descent == | ||
| Line 57: | Line 90: | ||
Main article: [[Fisher Linear Discriminant_Old Kiwi]] | Main article: [[Fisher Linear Discriminant_Old Kiwi]] | ||
| − | |||
| − | |||
| − | |||
Fischer's Linear Discriminant solves a dual problem: Traditionally, we have defined a separating hyperplane. Fischer's linear discriminant defines a projection which reduced the data to a single dimension. | Fischer's Linear Discriminant solves a dual problem: Traditionally, we have defined a separating hyperplane. Fischer's linear discriminant defines a projection which reduced the data to a single dimension. | ||
Fischer's Linear Discriminant optimizes the between class-spread. | Fischer's Linear Discriminant optimizes the between class-spread. | ||
| − | + | ---- | |
| − | + | [[ECE662:BoutinSpring08_Old_Kiwi|Back to ECE662, Spring 2008, Prof. Boutin]] | |
| − | + | [[Category:Lecture Notes]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [ | + | |
Latest revision as of 08:48, 17 January 2013
Lecture 10, ECE662: Decision Theory
Lecture notes for ECE662 Spring 2008, Prof. Boutin.
Other lectures: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
The perceptron algorithm maps an input to a single binary output value. For a proof of the Perceptron convergence theorem, see [PerceptronConvergenceTheorem]
First introduced in [Lecture 9]. The gradient descent algorithm used is discussed in [Lecture 10].
Contents
Gradient Descent
Main article: Gradient Descent_Old Kiwi
Consider the cost function $ J_p(\vec{c}) = \sum -\vec{c}y_i $, where $ y_i $ is the misclassified data.
We use the gradient descent procedure to minimize $ J_p(\vec{c}) $.
Compute $ \nabla J_p(\vec{c}) = ... = - \sum y_i $.
Follow basic gradient descent procedure:
- Initial guess $ \vec{c_1} $
- Then, update $ \vec{c_2} = \vec{c_1} - \eta(1) \nabla J_p(\vec{c}) $, where $ \eta(1) $ is the step size
- Iterate $ \vec{c_{k+1}} = \vec{c_{k}} - \eta(k) \nabla J_p(\vec{c}) $until it "converges"
( e.g when $ \eta(k) \nabla J_p(\vec{c}) $< threshold )
Gradient Descent in the Perceptron Algorithm
- Theorem: If samples are linearly separable, then the "batch [perceptron]" iterative algorithm. The proof of this theorem, PerceptronConvergenceTheorem, is due to Novikoff (1962).
$ \vec{c_{k+1}} = \vec{c_k} + cst \sum y_i $, where $ y_i $ is the misclassified data, terminates after a finite number of steps.
But, in practice, we do not have linear separable data. So instead, we use the Least Squares Procedure.
We want $ \vec{c} \cdot y_i > 0 $, for all samples $ y_i $. This is a linear inequality problem which is usually hard to solve. Therefore, we need to convert this problem into a linear equality problem.
We choose $ b_i $ > 0 and solve $ \vec{c} \cdot y_i = b_i $, for all i
The matrix equation has the following form:
This can also be written as $ \vec{Y} \cdot \vec{c} = \vec{b} $
If d=n, and $ \vec{y_1} $,..., $ \vec{y_d} $ are "generic" ( i.e. determinant of $ \vec{Y} $ is not 0), then we "can" solve by matrix inversion.
If d > n, over-constrained system (there is no solution in the generic case). This is the case where there is more data than you need, and the information is contradictory. In this case, we seek to minimize $ || Y \vec{c} - \vec{b} ||_{L_2} $. The solution is given by $ \vec{c} = (Y^{\top}Y)^{-1}Y^{\top}b $, if $ |Y^{\top}y| \ne 0 $.
If $ |Y^{\top}y| = 0 $, $ \vec{c} = lim (Y^{\top}Y + \epsilon1)^{-1}Y^{\top}b $ always exists!
Fischer's Linear Discriminant
Main article: Fisher Linear Discriminant_Old Kiwi
Fischer's Linear Discriminant solves a dual problem: Traditionally, we have defined a separating hyperplane. Fischer's linear discriminant defines a projection which reduced the data to a single dimension.
Fischer's Linear Discriminant optimizes the between class-spread.