Homework 6, ECE438, Fall 2011, Prof. Boutin

Question 1

a)

$y[n]= \frac{x[n]+x[n-1]}{2}$

Applying Z-transform on both sides and grouping terms, we can obtain the transfer function

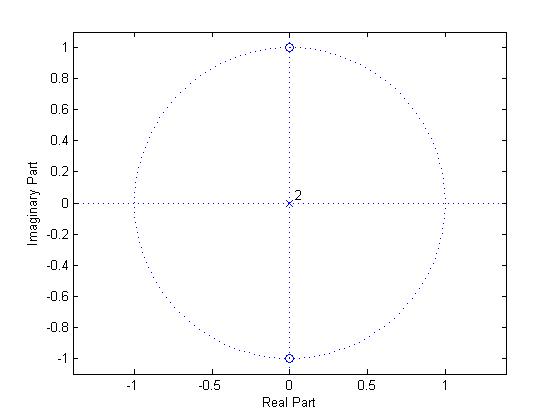
$\begin{align} Y[z]&= \frac{X[z]+X[z].z^{-1}}{2} \\ \frac{Y[z]}{X[z]}&= \frac{1+z^{-1}}{2} \\ H[z] &= \frac{1+z^{-1}}{2} \\ \end{align}$

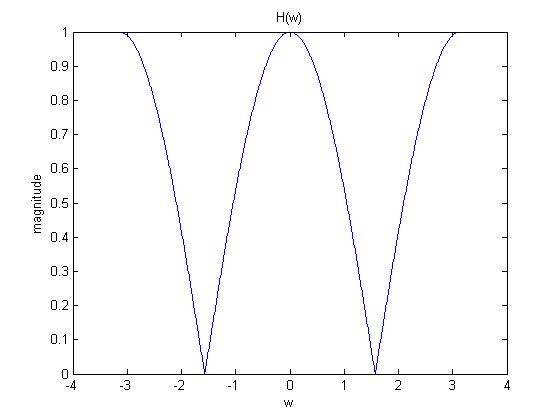
Frequency Response $H(\omega)$ $\begin{align} H[e^{j\omega }] &= \frac{1+e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}+e^{-j\frac{\omega }{2}}}{2} \right) \\ &= e^{-j\frac{\omega }{2}} cos \left( \frac{\omega }{2} \right) \\ \end{align}$

b)

$y[n]= \frac{x[n]-x[n-1]}{2}$

Applying Z-transform on both sides and grouping terms, we can obtain the transfer function

$\begin{align} Y[z]&= \frac{X[z]-X[z].z^{-1}}{2} \\ \frac{Y_2[z]}{X[z]}&= \frac{1-z^{-1}}{2} \\ H[z] &= \frac{1-z^{-1}}{2} \\ \end{align}$

Frequency Response $H(\omega)$ $\begin{align} H[e^{j\omega }] &= \frac{1-e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2} \right) \\ &= je^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2j} \right) \\ &= je^{-j\frac{\omega }{2}} sin \left( \frac{\omega }{2} \right) \\ \end{align}$