| Line 5: | Line 5: | ||
==Question 1== | ==Question 1== | ||
| − | Pick a note frequency <span class="texhtml">''f''<sub>0</sub> = 392''H | + | Pick a note frequency <span class="texhtml">''f''<sub>0</sub> = 392''H'''z''</span> |
{| | {| | ||
|- | |- | ||
| − | | <span class="texhtml">''x''(''t'') = | + | | <span class="texhtml">''x''(''t'') = 'c''o''s'(2π''f''<sub>0</sub>''t'') = 'c''o''s'(2π * 392''t'')</span> |
|- | |- | ||
| <math>a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000}</math> | | <math>a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000}</math> | ||
| Line 99: | Line 99: | ||
(1) <math>x[n]=a^{n+1}u[n-1],\ a>0</math> | (1) <math>x[n]=a^{n+1}u[n-1],\ a>0</math> | ||
| + | |||
| + | Compute Z transform | ||
<math>\begin{align} | <math>\begin{align} | ||
| Line 107: | Line 109: | ||
\end{align}</math> | \end{align}</math> | ||
| + | with ROC: <math>|z|>a</math> | ||
| + | |||
| + | Compute Inverse Z transform | ||
| + | |||
| + | The power series expansion of the given function is | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X(z) &= a^2 z^{-1}\sum_{n=0}^{\infty} a^n z^{-n} \\ | ||
| + | &= a\sum_{n=0}^{\infty} a^{n+1}z^{-n-1} | ||
| + | \end{align}</math> | ||
| + | |||
| + | Substitute n=m-1 | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X(z) &= a\sum_{m=1}^{\infty} a^{m}z^{-m} \\ | ||
| + | &= \sum_{m=-\infty}^{\infty} a^{m+1}u[m-1]z^{-m},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} | ||
| + | \end{align}</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | x[n] &= a^{n+1} u[n-1] | ||
| + | \end{align}</math> | ||
---- | ---- | ||
[[Hw2_ECE438F11|Back to Homework2]] | [[Hw2_ECE438F11|Back to Homework2]] | ||
[[2011_Fall_ECE_438_Boutin|Back to ECE438, Fall 2011, Prof. Boutin]] | [[2011_Fall_ECE_438_Boutin|Back to ECE438, Fall 2011, Prof. Boutin]] | ||
Revision as of 16:55, 13 September 2011
Homework 2, ECE438, Fall 2011, Prof. Boutin
Question 1
Pick a note frequency f0 = 392Hz
| x(t) = 'cos'(2πf0t) = 'cos'(2π * 392t) |
| $ a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000} $ |
| $ 2f_0<\frac{1}{T_1}, \ No\ aliasing\ occurs. $ |
$ \begin{align} x_1(n) &=x(nT_1)=cos(2\pi *392nT_1)=cos(2\pi *\frac{392}{1000}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{1000}n} + e^{j2\pi *\frac{392}{1000}n} \right) \\ \end{align} $
| $ 0<2\pi *\frac{392}{1000}<\pi $ |
| $ -\pi<-2\pi *\frac{392}{1000}<0 $ |
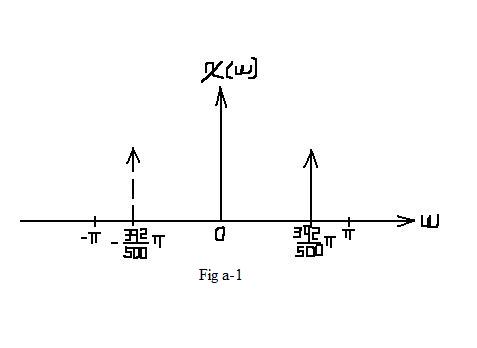
$ \begin{align} \mathcal{X}_1(\omega) &=2\pi *\frac{1}{2} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ &=\pi \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ \end{align} $
| $ for\ all\ \omega $ |
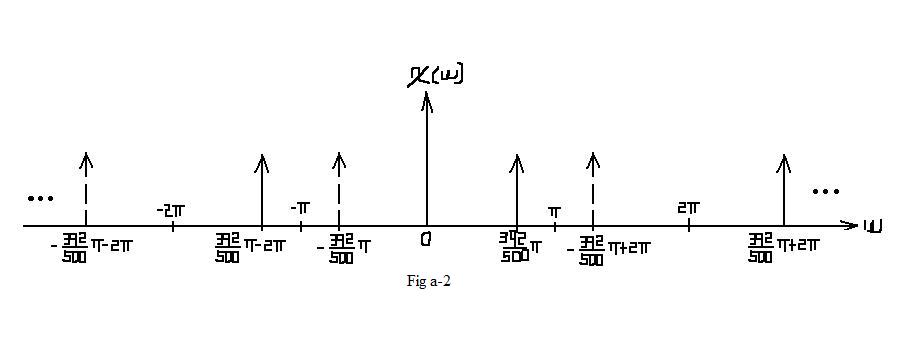
| $ \mathcal{X}_1(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] $ |
| In this situation, no aliasing occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum remains the same as Fig a-1. |
| $ b.\ Assign\ sampling\ period\ T_2=\frac{1}{500} $ |
| $ 2f_0>\frac{1}{T_2}, \ Aliasing\ occurs. $ |
$ \begin{align} x_2(n) &=x(nT_2)=cos(2\pi *392nT_2)=cos(2\pi *\frac{392}{500}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{500}n} + e^{j2\pi *\frac{392}{500}n} \right) \\ \end{align} $
| $ \pi<2\pi *\frac{392}{500}<2\pi $ |
| $ -2\pi<-2\pi *\frac{392}{500}<\pi $ |
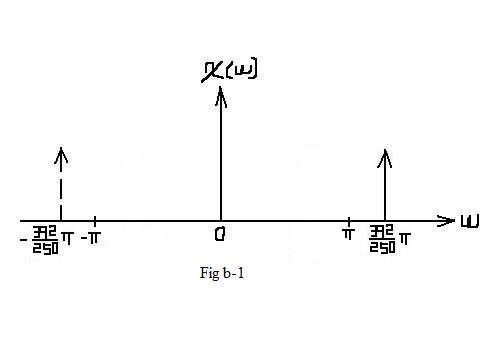
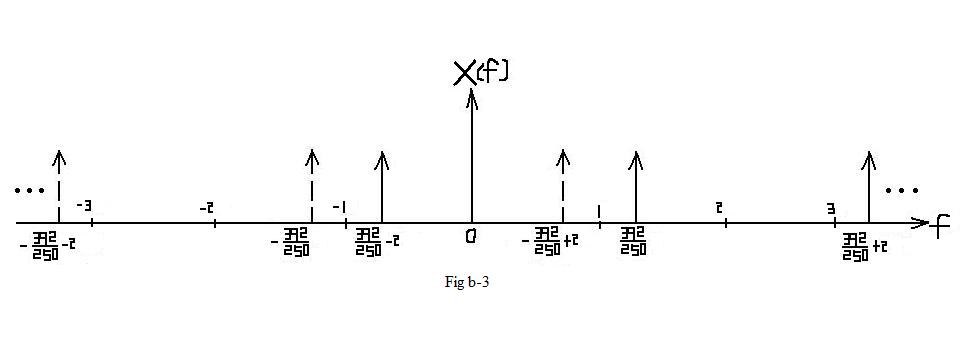
| $ \mathcal{X}_2(\omega)=\pi \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
| $ X_2(f)=\frac{1}{2}\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
| $ for\ all\ \omega $ |
| $ \mathcal{X}_2(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
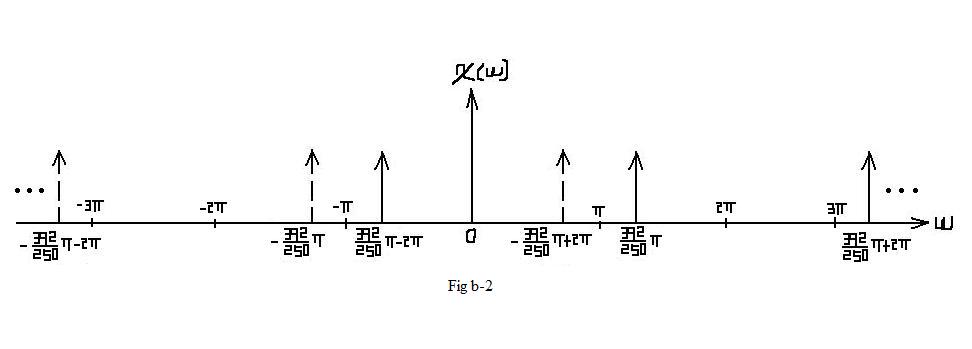
| $ X_2(f)=\frac{1}{2}rep_2\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
| In this situation, aliasing DO occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum is different from Fig b-1. |
Question 2
(1) $ x[n]=a^{n+1}u[n-1],\ a>0 $
Compute Z transform
$ \begin{align} X(z) &= \sum_{n=-\infty}^{\infty} x[n]z^{-n} \\ &= \sum_{n=-\infty}^{\infty} a^{n+1} u[n-1]z^{-n} \\ &= a\sum_{n=1}^{\infty} a^{n}z^{-n} \\ &= \frac{a^2z^{-1}}{1-az^{-1}} \end{align} $
with ROC: $ |z|>a $
Compute Inverse Z transform
The power series expansion of the given function is
$ \begin{align} X(z) &= a^2 z^{-1}\sum_{n=0}^{\infty} a^n z^{-n} \\ &= a\sum_{n=0}^{\infty} a^{n+1}z^{-n-1} \end{align} $
Substitute n=m-1
$ \begin{align} X(z) &= a\sum_{m=1}^{\infty} a^{m}z^{-m} \\ &= \sum_{m=-\infty}^{\infty} a^{m+1}u[m-1]z^{-m},\ \text{and by comparison with } X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} \end{align} $
$ \begin{align} x[n] &= a^{n+1} u[n-1] \end{align} $