| Line 17: | Line 17: | ||
=Coordinate Rotation= | =Coordinate Rotation= | ||
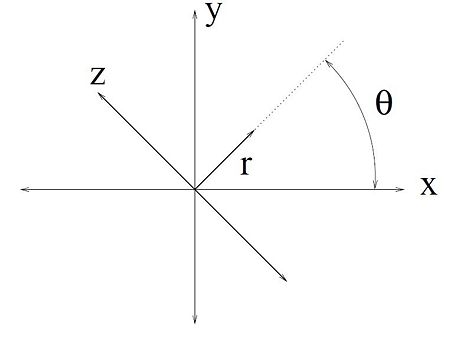
| − | To accommodate the multitude of angles that scans will we taken at, we will introduce a new coordinate system to work with, <math>(r,z)</math>. The relationship between <math>(x,y)</math> and <math>(r,z)</math> is shown below. The geometric meaning of <math>(r,z)</math> is shown in Figure 1. <br /> | + | To accommodate the multitude of angles that scans will we taken at, we will introduce a new coordinate system to work with, <math>(r,z)</math>. The relationship between <math>(x,y)</math> and <math>(r,z)</math> is shown below. The <math>(r,z)</math> axes are rotated counterclockwise by <math>\theta</math> relative to the <math>(x,y)</math> axes. The geometric meaning of <math>(r,z)</math> is shown in Figure 1. <br /> |
<math>\begin{bmatrix} | <math>\begin{bmatrix} | ||
x \\ | x \\ | ||
| Line 30: | Line 30: | ||
\sin(\theta) & \cos(\theta) | \sin(\theta) & \cos(\theta) | ||
\end{bmatrix}</math><br/> | \end{bmatrix}</math><br/> | ||
| + | [[Image:GeometricInterpretation.jpg|450px|thumb|left|Fig 1: Geometric Interpretation of Rotated Coordinate System]] | ||
| + | |||
| + | |||
---- | ---- | ||
Revision as of 19:24, 17 December 2014
Coordinate Rotation and the Radon Transform
A slecture by ECE student Sahil Sanghani
Partly based on the ECE 637 material of Professor Bouman.
Introduction
A Radon Transform is an integral that allows the calculation of the projections of an object as it is scanned. Since the scanner rotates as it takes data, the projections will have to be calculated at various angles. Thus coordinate rotation is an essential topic for tomographic reconstruction because it allows the calculation of the Radon Transform.
Coordinate Rotation
To accommodate the multitude of angles that scans will we taken at, we will introduce a new coordinate system to work with, $ (r,z) $. The relationship between $ (x,y) $ and $ (r,z) $ is shown below. The $ (r,z) $ axes are rotated counterclockwise by $ \theta $ relative to the $ (x,y) $ axes. The geometric meaning of $ (r,z) $ is shown in Figure 1.
$ \begin{bmatrix} x \\ y \end{bmatrix} = \mathbf{A_{\theta}}\begin{bmatrix} r \\ z \end{bmatrix} $
Where $ A_\theta $ is the counterclockwise rotation matrix
$ \mathbf{A_{\theta}}=\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} $
References:
[1] C. A. Bouman. ECE 637. Class Lecture. Digital Image Processing I. Faculty of Electrical Engineering, Purdue University. Spring 2013.