| Line 33: | Line 33: | ||
Above equation, however, becomes trivial since <math>p(x|x')</math> forms a delta function centered at x. This condition gives out the positive number <math>P_s</math> which is the probability that any sample falls within a hypersphere <math>\mathbb{S}</math> centered about x | Above equation, however, becomes trivial since <math>p(x|x')</math> forms a delta function centered at x. This condition gives out the positive number <math>P_s</math> which is the probability that any sample falls within a hypersphere <math>\mathbb{S}</math> centered about x | ||
<center><math>P_s = \int_{x'\in \mathbb{S}}p(x')dx'</math></center> | <center><math>P_s = \int_{x'\in \mathbb{S}}p(x')dx'</math></center> | ||
| − | This means that the probability that independently drawn samples fall outside of hypersphere <math>\mathbb{S}</math> is <math>(1-P_s)^n</math>. This equation will approach zero as n goes to infinity. This proves that x' converges to x with infinite number of samples. | + | This means that the probability that independently drawn samples fall outside of hypersphere <math>\mathbb{S}</math> is <math>(1-P_s)^n</math>. This equation will approach zero as n goes to infinity. This proves that x' converges to x with infinite number of samples.<br> |
| + | asdf | ||
---- | ---- | ||
=='''Metrics Type'''== | =='''Metrics Type'''== | ||
Revision as of 08:51, 30 April 2014
Nearest Neighbor Method (Still working on it. Please do not put any comments yet. Thank you)
A slecture by Sang Ho Yoon
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
Contents
Introduction
In this slecture, basic principles of implementing nearest neighbor rule will be covered. The error related to the nearest neighbor rule will be discussed in detail including convergence, error rate, and error bound. Since the nearest neighbor rule relies on metric function between patterns, the properties of metrics will be studied in detail. Example of different metrics will be introduced with its characteristics. The representative of real application such as body posture recognition using Procrustes metric could be a good example to understand the nearest neighbor rule.----
Nearest Neighbor Basic Principle
Let's consider a testing sample x. Based on labeled training sample $ D^n = x_{1},... ,x_{n}, $ the nearest neighbor technique will find the closest point x' to x. Then we assign the class of x' to x. This is how the classification based on the nearest neighbor rule is processed. Although this rule is very simple, it is also reasonable. The label $ \theta' $ used in the nearest neighbor is random variable which means $\theta' = w_{i}$ is same as a posteriori probability $P(w_{i}|x').$ If sample sizes are big enough, it could be assumed that x' is sufficiently close to x that $ P(w_{i}|x') = P(w_{i}|x). $ Using the nearest neighbor rule, we could get high accuracy classification if sample sizes are guaranteed. In other words, the nearest neighbor rule is matching perfectly with probabilities in nature.
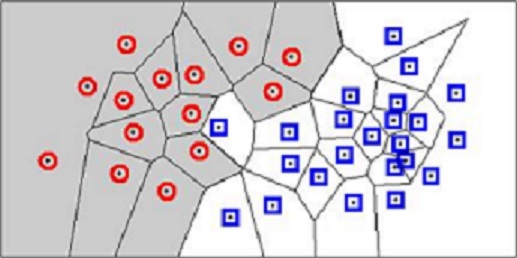
Error Rate & Bound using NN
In order to find the error rate and bound related to the nearest neighbor rule, we need to confirm the convergence of the nearest neighbor as sample increases to the infinity. We set $ P = \lim_{n \to \infty}P_n(e) $. Then, we set infinite sample conditional average probability of error as $ P(e|x) $. Using this the unconditional average probability of error which indicates the average error according to training samples can be shown as
Since minimum error caused by the nearest neighbor cannot be lower than error from Bayes decision rule, the minimum possible value of the error $ P^*(e|x) $ can be represented as
In real application, we cannot guarantee that sufficient number of samples are used for training. In some cases, small sample sizes could lead to an accidental characteristics where it will eventually lead to an error. The decision will be made on based on this nearest neighbor which introduces a conditional probability error $ P(e|x,x') $. Again, averaging over x', we will get
Above equation, however, becomes trivial since $ p(x|x') $ forms a delta function centered at x. This condition gives out the positive number $ P_s $ which is the probability that any sample falls within a hypersphere $ \mathbb{S} $ centered about x
This means that the probability that independently drawn samples fall outside of hypersphere $ \mathbb{S} $ is $ (1-P_s)^n $. This equation will approach zero as n goes to infinity. This proves that x' converges to x with infinite number of samples.
asdf
Metrics Type
However, the closest distance between x' and x is determined by which metrics are used for feature space. A "metric" on a space S is a function $ D: S\times S\rightarrow \mathbb{R} $ which has following 4 properties:
- Non-negativity : $ D(\vec{x_{1}},\vec{x_{2}}) \geq 0, \forall \vec{x_{1}},\vec{x_{2}} \in S $
- Symmetry : $ D(\vec{x_{1}},\vec{x_{2}}) = D(\vec{x_{2}},\vec{x_{1}}), \forall \vec{x_{1}},\vec{x_{2}} \in S $
- Reflexivity : $ D(\vec{x},\vec{x}) = 0, \forall \vec{x} \in S $
- Triangle Inequality : $ D(\vec{x_{1}},\vec{x_{2}}) + D(\vec{x_{2}},\vec{x_{3}}) \geq D(\vec{x_{1}},\vec{x_{3}}), \forall \vec{x_{1}},\vec{x_{2}},\vec{x_{3}} \in S $
Real Application
References
Questions and comments
If you have any questions, comments, etc. please post them on this page.

