Difference between revisions of "ECE600 F13 set theory review mhossain" - Rhea

Revision as of 22:12, 23 September 2013

Random Variables and Signals

Subtopic 1: Set Theory Review

Definitions and Notation

Definition $\qquad$ A set is a collection of objects called elements, numbers or points.

Notation $\qquad$ $\omega$ ∈ $$ A $$ means $\omega$ is an element of the set $$ A $$ . $\omega$ ∉ $$ A $$ means $\omega$ is not in the set $$ A $$ .

There are two common ways to specify a set:

Explicitly list all elements, e.g. $\{1,2,3,4,5,6\}$
Specify a rule for membership, e.g. $A=\{\omega$ ∈ $$ Z:1 $$ ≤ $\omega$ ≤ $6\}$ , i.e. the set of all integers between 1 and 6 inclusive. I prefer this notation for large or infinite sets.

Note that there is always a set that contains every possible element of interest. This set, along with some structure imposed upon the set, is called a space, denoted

\mathcal{S}

\qquad

or

\qquad

\Omega .\

Definition $\qquad$ Let $$ A $$ and $$ B $$ be two sets. Then,

\begin{align} A = B &\Longleftrightarrow \omega \in A \Rightarrow \omega \in B \;\and\; \omega \in B \Rightarrow \omega \in A \\ &\Longleftrightarrow A \subset B \;\and\; B \subset A \end{align}

The proof that the second statement is equivalent is trivial and follows from the definition of the term subset, which is presented shortly.

If $$ A $$ and $$ B $$ are not equal, we write

A\neq B

Definition $\qquad$ If $\omega$ ∈ $$ A $$ ⇒ $\omega$ ∈ $$ B $$ , then $$ A $$ is said to be a subset of $$ B $$ . if If $$ B $$ contains atleast one element that is not in $$ A $$ , then $$ A $$ is a proper subset of $$ B $$ . We will simply call $$ A $$ a subset of $$ B $$ in either case, and write $$ A $$ ⊂ $$ B $$ .

Definition $\qquad$ the set with not elements is called the empty set, or null set and is denoted Ø or {}.

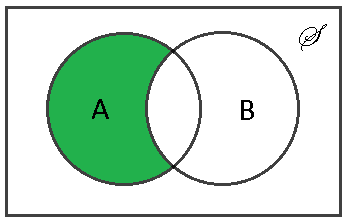
Venn Diagrams

A Venn diagram is a graphical representation of sets. It can be useful to gain insight into a problem, but cannot be used as a proof.

Fig 1: An example of a Venn diagram

Set Operations

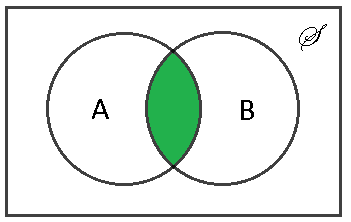
Definition $\qquad$ The intersection of sets $$ A $$ and is defined as

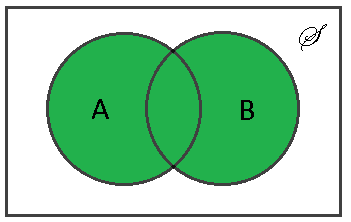
A\cap B \equiv \{\omega \in \mathcal{S}: \omega \in A \and \omega \in B\}

Fig 2: A∩B is shown in green

Definition $\qquad$ The union of sets $$ A $$ and is defined as

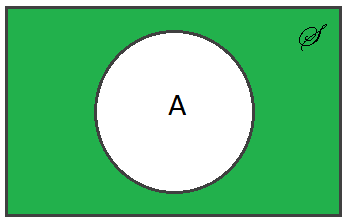
A\cup B \equiv \{\omega \in \mathcal{S}: \omega \in A \or \omega \in B \; or\; both\}

Fig 3: A∪B is shown in green

Definition $\qquad$ The complement of a set $$ A $$ , denoted $$ A^c $$ , Ā, or A' is defined as

A^c \equiv \{\omega \in \mathcal{S}: \omega \notin A\}

Fig 4:

$ A^c $

is shown in green

Definition $\qquad$ The set difference $$ A-B $$ or A\B is defined as

A-B \equiv \{\omega \in \mathcal{S}: \omega \in A\and \omega \notin B\}

Note that

A-B=A\cap B^c

Fig 5:

$ A-B $

is shown in green

Definition $\qquad$ Sets $$ A $$ and $$ B $$ are disjoint if $$ A $$ and $$ B $$ have not elements in common ie

A\cap B = \varnothing

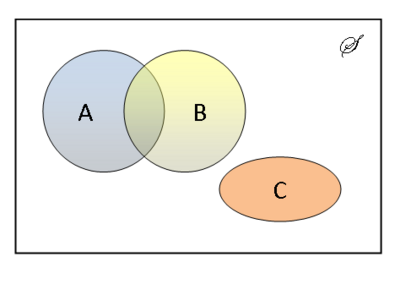
In figure 1, A and C are disjoint. B and C are also disjoint.

Algebra of Sets

Union is commutative ⇔ A ∪ B = B ∪ A
Intersection is commutative ⇔ A ∩ B = B ∩ A
Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C
Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C
Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(A')' = A
DeMorgan's Law: (A ∩ B)' = A' ∪ B'
DeMorgan's Law: (A ∪ B)' = A' ∩ B'
S' = Ø, where S is the sample space
A ∩ S = A
A ∩ Ø = Ø
A ∪ S = S
A ∪ Ø = A
A ∪ A' = S
A ∩ A' = Ø

A Note on Sets of Different Sizes

We can categorize the sets we encounter three ways:

A set $$ A $$ is finite if it contains an finite number of elements, i.e. the number of elements in the set is some natural number $$ n $$ . Then we can list the elements in $$ A $$ ; e.g. $A = \{x_1,...,x_n\}$ .

A set is countable if its elements can be put into a one-to-one correspondence (a bijection) with the integers. In this course when, we say countable, we mean countably infinite. We may write $A=\{x_1,x_2,...\}$ . The set of rationals is a countable set.

A set is uncountable if it is not finite or countable. A set that is uncountable cannot be written as $\{x_1,x_2,...\}$ . Note that the set of reals as well as any interval in R is uncountable.

If you are interested to learn more about countable and uncountable sets, you may find this Math Squad tutorial useful.

We will often consider indexed collections of sets such as

\{A_i, i\in I\}

where $$ I $$ is called the index set.

The index set can be

finite: $I=\{1,...,n\}$ for some finite natural number n so that the collection of sets is $I=\{A_1,...,A_n\}$

countable: $$ I $$ is the set of natural numbers i.e. $I=\{1,2,3,...\}$ , so the collection is $\{A)_1,A_2,A_3,...\}$

uncountable: so the collection is $\{A_{\alpha}, \alpha$ ∈ $I\}$ cfor an uncountable set $$ I $$ . If $$ I=R $$ , the set of reals, then the set in the collection can be written as $A_{\alpha}$ for some real number $\alpha$

Definition $\qquad$ The union of an indexed family of sets is defined as

\bigcup_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; for \; at \; least \; one \; i\in I \}

Note that if $$ I $$ is finite, we can write the union as

\bigcup_{i \in I}^n A_i

If $$ I $$ is countable, we can write the union as

\bigcup_{i \in I}^{\infty} A_i

If $$ I $$ is uncountable, we can write the union as

\bigcup_{i \in I} A_i

as in the definition.

Definition $\qquad$ The intersection of an indexed family of sets is defined as

\bigcap_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; \forall \; i\in I \}

Note that if $$ I $$ is finite, we can write the intersection as

\bigcap_{i \in I}^n A_i

If $$ I $$ is countable, we can write the intersection as

\bigcap_{i \in I}^{\infty} A_i

If $$ I $$ is uncountable, we can write the intersection as

\bigcap_{i \in I} A_i

.

Definition $\qquad$ $\{A_i, i$ ∈ $$ I $$ is disjoint if $$ A_i $$ ∩ $$ A_j $$ = Ø ∀ i,j∈I, i≠j.

Definition $\qquad$ the collection $\{A_i, i$ ∈ $$ I $$ is a \partition of S, the sample space, if it is disjoint and if

\bigcup_{i \in I} A_i = \mathcal{S}

References

M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

@@ Line 95: / Line 95: @@
 ==Algebra of Sets==
+# Union is commutative ⇔ A ∪ B = B ∪ A
+# Intersection is commutative ⇔ A ∩ B = B ∩ A
+# Union is associative ⇔ A ∪ (B ∪ C) = (A ∪ B) ∪ C
+# Intersection is associative ⇔ A ∩ (B ∩ C) = (A ∩ B) ∩ C
+# Intersection is distributive over union ⇔ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
+# Union is distributive over intersection ⇔ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
+# (A')' = A
+# DeMorgan's Law: (A ∩ B)' = A' ∪ B'
+# DeMorgan's Law: (A ∪ B)' = A' ∩ B'
+# ''S''' = Ø, where ''S'' is the sample space
+# A ∩ S = A
+# A ∩ Ø = Ø
+# A ∪ S = S
+# A ∪ Ø = A
+# A ∪ A' = S
+# A ∩ A' = Ø
+----
+==A Note on Sets of Different Sizes==
+We can categorize the sets we encounter three ways:
+* A set <math>A</math> is '''finite''' if it contains an finite number of elements, i.e. the number of elements in the set is some natural number <math>n</math>. Then we can list the elements in <math>A</math>; e.g. <math>A = \{x_1,...,x_n\}</math>.
+* A set is '''countable''' if its elements can be put into a one-to-one correspondence (a [[Math_Squad_infinity_review_of_set_theory_function_mhossain_S13|bijection]]) with the integers. In this course when, we say countable, we mean countably infinite. We may write <math>A=\{x_1,x_2,...\}</math>. The set of rationals is a countable set.
+* A set is '''uncountable''' if it is not finite or countable. A set that is uncountable cannot be written as <math>\{x_1,x_2,...\}</math>. Note that the set of reals as well as any interval in R is uncountable.
+If you are interested to learn more about countable and uncountable sets, you may find this [[Math_Squad_infinity_review_of_set_theory_countablity_mhossain_S13|Math Squad tutorial]] useful.
+We will often consider indexed collections of sets such as <br/>
+<center><math>\{A_i, i\in I\}</math></center>
+where <math>I</math> is called the index set.
+The index set can be
+* finite: <math>I=\{1,...,n\}</math> for some finite natural number n so that the collection of sets is <math>I=\{A_1,...,A_n\}</math>
+* countable: <math>I</math> is the set of natural numbers i.e. <math>I=\{1,2,3,...\}</math>, so the collection is <math>\{A)_1,A_2,A_3,...\}</math>
+*uncountable: so the collection is <math>\{A_{\alpha}, \alpha</math>∈<math>I\}</math>cfor an uncountable set <math>I</math>. If <math>I=R</math>, the set of reals, then the set in the collection can be written as <math>A_{\alpha}</math> for some real number <math>
+\alpha</math>
+'''Definition''' <math>\qquad</math> '''The union of an indexed family of sets''' is defined as <br/>
+<center><math>\bigcup_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; for \; at \; least \; one \; i\in I \}</math></center><br/>
+Note that if <math>I</math> is finite, we can write the union as <br/>
+<center><math>\bigcup_{i \in I}^n A_i</math></center>
+If <math>I</math> is countable, we can write the union as <br/>
+<center><math>\bigcup_{i \in I}^{\infty} A_i</math></center>
+If <math>I</math> is uncountable, we can write the union as <br/>
+<center><math>\bigcup_{i \in I} A_i</math></center> as in the definition.
+'''Definition''' <math>\qquad</math> '''The intersection of an indexed family of sets''' is defined as <br/>
+<center><math>\bigcap_{i \in I} A_i = \{\omega \in \mathcal{S}:\omega\in A_i \; \forall \; i\in I \}</math></center><br/>
+Note that if <math>I</math> is finite, we can write the intersection as <br/>
+<center><math>\bigcap_{i \in I}^n A_i</math></center>
+If <math>I</math> is countable, we can write the intersection as <br/>
+<center><math>\bigcap_{i \in I}^{\infty} A_i</math></center>
+If <math>I</math> is uncountable, we can write the intersection as <br/>
+<center><math>\bigcap_{i \in I} A_i</math></center>.
+'''Definition''' <math>\qquad</math> <math>\{A_i, i</math>∈<math>I</math> is '''disjoint''' if <math>A_i</math>∩<math>A_j</math> = Ø ∀ i,j∈I, i≠j.
+'''Definition''' <math>\qquad</math> the collection <math>\{A_i, i</math>∈<math>I</math> is a \'''partition''' of ''S'', the sample space, if it is disjoint and if
+<center><math>\bigcup_{i \in I} A_i = \mathcal{S}</math></center>