Difference between revisions of "ECE600 F13 Expectation mhossain" - Rhea

Latest revision as of 12:12, 21 May 2014

Topic 9: Expectation

Thus far, we have learned how to represent the probabilistic behavior of a random variable X using the density function f $$ _X $$ or the mass function p $$ _X $$ .
Sometimes, we want to describe X probabilistically using only a small number of parameters. The expectation is often used to do this.

Definition $\qquad$ the expected value of continuous random variable X is defined as

E[X] = \int_{-\infty}^{\infty}xf_X(x)dx

Definition $\qquad$ the expected value of discrete random variable X is defined as

E[X] = \sum_{x\in\mathcal R_X}xp_X(x)

where $$ R_X $$ is the range space of X.

Note:

E[X] is also known as the mean of X. Other notation for E[X] include:

EX,\;\overline{X},\;m_X,\;\mu_X

The equation defining E[X] for discrete X could have been derived from that for continuous X, using the density function f $$ _X $$ containing $\delta$ -functions.

Example $\qquad$ X is an exponential random variable. find E[X].

f_X(x) = \lambda e^{-\lambda x}u(x) \

\begin{align} E[X] &= \int_{-\infty}^{\infty}xf_X(x)dx \\ &= \int_{0}^{\infty}x\lambda e^{-\lambda x}dx \\ &= \frac{1}{\lambda} \end{align}

Let $\mu = 1/\lambda$ . We often write

f_X(x) = \frac{1}{\mu} e^{-\frac{1}{\mu}x}u(x) \

Example $\qquad$ X is a uniform discrete random varibable with $$ R_X $$ = {1,...,n}. Then,

\begin{align} E[X]&=\sum_{k=1}^n\frac{k}{n} \\ &=\frac{1}{n}\sum_{k=1}^n k \\ \\ &= \frac{1}{n}\left(\frac{1}{2}\right)(n)(n+1) \\ \\ &=\frac{n+1}{2} \end{align}

Having defined E[X], we will now consider more general E[g(X)] for a function g:R → R.

Let Y = g(X). What is E[Y]? From previous definitions:

E[Y]=\int_{-\infty}^{\infty}yf_Y(y)dy

or

E[Y] = \sum_{y\in\mathcal R_Y}yp_Y(y)

We can find the expectation of Y by first finding f $$ _Y $$ or p $$ _Y $$ in terms of g and f $$ _X $$ or p $$ _X $$ . Alternatively, it can be shown that

E[Y]=E[g(X)]=\int_{-\infty}^{\infty}g(x)f_X(x)dx

or

E[Y] = E[g(X)]=\sum_{y\in\mathcal R_X}g(x)p_X(x)

See Papoulis for a proof of the above.

Two important cases or functions g:

g(x) = x. Then E[g(X)] = E[X]
g(x) = (x - $\mu_X)^2$ . Then E[g(X)] = E[(X - $\mu_X)^2$ ]

E[g(X)] = \int_{-\infty}^{\infty}(x-\mu_X)^2f_X(x)dx

or

E[g(X)] = \sum_{x\in\mathcal R_x}(x-\mu_X)^2p_X(x)

Note: $\qquad$ E[(X - $\mu_X)^2$ ] is called the variance of X and is often denoted $\sigma_X$ $$ ^2 $$ . The positive square root, denoted $\sigma_X$ , is called the standard deviation of X.

Important property of E[]:
Let g $$ _1 $$ :R → R; g $$ _2 $$ :R → R; $\alpha,\beta$ ∈ R. Then

E[\alpha g_1(X) +\beta g_2(X)] = \alpha E[g_1(X)]+\beta E[g_2(X)] \

So E[] is a linear operator. The proof follows from the linearity of integration.

Important property of Var():

Var(X) = E[X^2]-\mu_X^2

Proof:

\begin{align} E[(X-\mu_X)^2]&=E[X^2-2X\mu_X+\mu_X^2] \\ &=E[X^2]-2\mu_XE[X]+E[\mu_X^2] \\ &=E[X^2]-2\mu_X^2+\mu_X^2 \\ &=E[X^2]-\mu_X^2 \end{align}

Example $\qquad$ X is Gaussian N( $\mu,\sigma^2$ ). Find E[X] and Var(X).

E[X] = \int_{-\infty}^{\infty}\frac{x}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx

Let r = x - $\mu$ . Then

E[X] = \int_{-\infty}^{\infty}\frac{r}{\sqrt{2\pi}\sigma}e^{-\frac{r^2}{2\sigma^2}}dr\;+\; \mu\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{r^2}{2\sigma^2}}dr

First term: Integrating an odd function over (-∞,∞) ⇒ first term is 0.
Second term: Integrating a Gaussian pdf over (-∞,∞) gives one ⇒ second term is $\mu$ .
So E[X] = $\mu$

E[X^2] = \int_{-\infty}^{\infty}\frac{x^2}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx

Using integration by parts (proof), we see that this integral evaluates to $\sigma^2+\mu^2$ . So,

Var(X) = \sigma^2+\mu^2-\mu^2 = \sigma^2

Example $\qquad$ X is Poisson with parameter $\lambda$ . Find E[X] and Var(X).

\begin{align} E[X] &= \sum_{k=0}^{\infty}k\frac{e^{-\lambda}\lambda^k}{k!} \\ &= \sum_{k=1}^{\infty}\frac{e^{-\lambda}\lambda^k}{(k-1)!} \\ &= \lambda\sum_{k=0}^{\infty}e^{-\lambda}\frac{\lambda^k}{k!} \\ &= \lambda \end{align}

\begin{align} E[X^2] &= \sum_{k=0}^{\infty}k^2\frac{e^{-\lambda}\lambda^k}{k!} \\ &= \sum_{k=0}^{\infty}(k+1)\frac{e^{-\lambda}\lambda^{k+1}}{k!} \\ &= \lambda\sum_{k=0}^{\infty}\frac{ke^{-\lambda}\lambda^k}{k!}\;+\;\lambda\sum_{k=0}^{\infty}\frac{e^{-\lambda}\lambda^k}{k!} \\ \\ &= \lambda E[X] + \lambda(1) \\ &= \lambda^2+\lambda \end{align}

So,
$E[X^2] = \lambda^2 +\lambda \$
$\Rightarrow Var(X) = \lambda^2 +\lambda - \lambda^2 = \lambda \$

Moments

Moments generalize mean and variance to nth order expectations.

Definition $\qquad$ the nth moment of random variable X is

\mu_n\equiv E[X^n]=\int_{-\infty}^{\infty}x^nf_X(x)dx\quad n=1,2,...

and the nth central moment of X is

v_n\equiv E[(X-\mu_X)^n] = \int_{-\infty}^{\infty}(x-\mu_X)^nf_X(x)dx\qquad n = 2,3,...

So

$\mu_1$ = E[X] mean
$\mu_2$ = E[X $$ ^2 $$ ] mean-square
v $$ _2 $$ = Var(X) variance

Conditional Expectation

For an event M ∈ F with P(M) > 0.

E[g(X)|M] = \int_{-\infty}^{\infty}g(x)f_X(x|M)dx

or

E[g(X)|M] = \sum_{x\in\mathcal R_x}g(x)p_X(x|M)dx

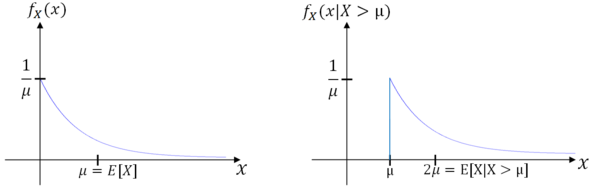
Example $\qquad$ X is an exponential random variable. Let M = {X > $\mu$ }. Find E[X|M]. Note that P(M) = P(X > $\mu$ ) and since $\mu$ > 0,

P(M) = P(X>\mu) =\int_{\mu}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}dx \;>\;0

It can be shown that

f_X(x|X>\mu) = \frac{1}{\mu}e^{-\frac{x-\mu}{\mu}}u(x-\mu)

Then,

\begin{align} E[X|X>\mu] &=\int_{\mu}^{\infty}\frac{x}{\mu}e^{-\frac{x-\mu}{\mu}} \\ &=2\mu \end{align}

Fig 1: Conditional Expectation; X is exponential.

References

M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.

Questions and comments

If you have any questions, comments, etc. please post them on this page

Back to all ECE 600 notes
Previous Topic: Functions of a Random Variable
Next Topic: Characteristic Functions

@@ Line 1: / Line 1: @@
 [[Category:ECE600]]
 [[Category:Lecture notes]]
+[[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]]<br/>
+[[ECE600_F13_rv_Functions_of_random_variable_mhossain|Previous Topic: Functions of a Random Variable]]<br/>
+[[ECE600_F13_Characteristic_Functions_mhossain|Next Topic: Characteristic Functions]]
+----
+[[Category:ECE600]]
+[[Category:probability]]
+[[Category:lecture notes]]
+[[Category:slecture]]
 <center><font size= 4>
-'''Random Variables and Signals'''
+[[ECE600_F13_notes_mhossain|'''The Comer Lectures on Random Variables and Signals''']]
 </font size>
+[https://www.projectrhea.org/learning/slectures.php Slectures] by [[user:Mhossain | Maliha Hossain]]
 <font size= 3> Topic 9: Expectation</font size>
 </center>
+----
 ----
+Thus far, we have learned how to represent the probabilistic behavior of a random variable X using the density function f<math>_X</math> or the mass function p<math>_X</math>. <br/>
-Thus far, we have learned how to represent the probabilistic behavior or random variables X using the density function f<math>_X</math> or the mass function p<math>_X</math>. <br/>
 Sometimes, we want to describe X probabilistically using only a small number of parameters. The expectation is often used to do this.
 '''Definition''' <math>\qquad</math> the '''expected value''' of continuous random variable X is defined as <br/>
-<center><math>E[X) = \int_{-\infty}^{\infty}xf_X(x)dx</math></center>
+<center><math>E[X] = \int_{-\infty}^{\infty}xf_X(x)dx</math></center>
@@ Line 27: / Line 38: @@
 *E[X] is also known as the mean of X. Other notation for E[X] include:<br/>
 <center><math> EX,\;\overline{X},\;m_X,\;\mu_X</math></center>
-*The equation defining E[X] for discrete X could have been derived from the continuous X, using the density function f<math>_X</math> containing <math>\delta</math>-functions.
+*The equation defining E[X] for discrete X could have been derived from that for continuous X, using the density function f<math>_X</math> containing <math>\delta</math>-functions.
 '''Example''' <math>\qquad</math> X is an exponential random variable. find E[X].<br/>
@@ Line 46: / Line 57: @@
 &=\frac{1}{n}\sum_{k=1}^n k \\
 \\
-&= \frac{1}{n}(\frac{1}{2})(n)(n+1) \\
+&= \frac{1}{n}\left(\frac{1}{2}\right)(n)(n+1) \\
 \\
 &=\frac{n+1}{2}
@@ Line 59: / Line 70: @@
 <math>E[Y] = \sum_{y\in\mathcal R_Y}yp_Y(y)</math></center>
-We can find this by first finding f<math>_Y</math> or p<math>_Y</math> in terms of g and f<math>_X,/math> or p<math>_X</math>. Alternatively, it can be shown that <br/>
+We can find the expectation of Y by first finding f<math>_Y</math> or p<math>_Y</math> in terms of g and f<math>_X</math> or p<math>_X</math>. Alternatively, it can be shown that <br/>
 <center><math>E[Y]=E[g(X)]=\int_{-\infty}^{\infty}g(x)f_X(x)dx</math><br/>
 or<br/>
 <math>E[Y] = E[g(X)]=\sum_{y\in\mathcal R_X}g(x)p_X(x)</math></center>
-See Papoulis for the proof of the above.
+See Papoulis for a proof of the above.
 Two important cases or functions g:
@@ Line 73: / Line 84: @@
 <math> E[g(X)] = \sum_{x\in\mathcal R_x}(x-\mu_X)^2p_X(x)</math></center>
-'''Note:''' <math>\qquad</math> E[(X - <math>\mu_X)^2</math>] is called the '''variance''' of X and is often denoted <math>\sigma_X</math><math>^2</math>. <math>\sigma_X</math> is called the standard deviation of X.
+'''Note:''' <math>\qquad</math> E[(X - <math>\mu_X)^2</math>] is called the '''variance''' of X and is often denoted <math>\sigma_X</math><math>^2</math>. The positive square root, denoted <math>\sigma_X</math>, is called the standard deviation of X.
 Important property of E[]:<br/>
-Let g<math>_1</math>:'''R''' → '''R'''; g<math>_2</math>:'''R''' → '''R'''; <math>\alpha,\beta</math> ∈ '''R''', Then <br/>
+Let g<math>_1</math>:'''R''' → '''R'''; g<math>_2</math>:'''R''' → '''R'''; <math>\alpha,\beta</math> ∈ '''R'''. Then <br/>
 <center><math>E[\alpha g_1(X) +\beta g_2(X)] = \alpha E[g_1(X)]+\beta E[g_2(X)] \ </math></center>
 So E[] is a linear operator. The [[Lineariy_of_expectation_proof_mhossain|proof]] follows from the linearity of integration.
@@ Line 84: / Line 95: @@
 Proof:
 <center><math>\begin{align}
-E[(X-\mu)^2]&=E[X^2-2X\mu_X+\mu_X^2] \\
+E[(X-\mu_X)^2]&=E[X^2-2X\mu_X+\mu_X^2] \\
 &=E[X^2]-2\mu_XE[X]+E[\mu_X^2] \\
 &=E[X^2]-2\mu_X^2+\mu_X^2 \\
@@ Line 91: / Line 102: @@
-'''Example''' <math>\qquad</math> X is Gaussian N(<math>\mu,\sigma^2</math>). Find E[X} and Var(X).<br/>
+'''Example''' <math>\qquad</math> X is Gaussian N(<math>\mu,\sigma^2</math>). Find E[X] and Var(X).<br/>
 <center><math>E[X] =  \int_{-\infty}^{\infty}\frac{x}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx</math></center>
 Let r = x - <math>\mu</math>. Then <br/>
@@ Line 100: / Line 111: @@
 <center><math>E[X^2] =  \int_{-\infty}^{\infty}\frac{x^2}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx</math></center>
-Using integration by parts, we see that this integral evaluates to <math>\sigma^2+\mu^2</math>. So, <br/>
+Using integration by parts (proof), we see that this integral evaluates to <math>\sigma^2+\mu^2</math>. So, <br/>
 <center><math>Var(X) = \sigma^2+\mu^2-\mu^2 = \sigma^2</math></center>
@@ Line 133: / Line 144: @@
 Moments generalize mean and variance to nth order expectations.
-'''Definition''' <math>\qquad</math> the '''nth order moment''' of random variable X is<br/>
+'''Definition''' <math>\qquad</math> the '''nth moment''' of random variable X is<br/>
 <center><math>\mu_n\equiv E[X^n]=\int_{-\infty}^{\infty}x^nf_X(x)dx\quad n=1,2,...</math></center>
@@ Line 186: / Line 197: @@
 ----
-[[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]]
+[[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]]<br/>
+[[ECE600_F13_rv_Functions_of_random_variable_mhossain|Previous Topic: Functions of a Random Variable]]<br/>
+[[ECE600_F13_Characteristic_Functions_mhossain|Next Topic: Characteristic Functions]]