(New page: Category:slecture Category:ECE438Fall2014Boutin Category:ECE Category:ECE438 Category:signal processing <center><font size= 4> Discrete-time Fourier transform (DTF...) |
|||
| Line 15: | Line 15: | ||
---- | ---- | ||
---- | ---- | ||
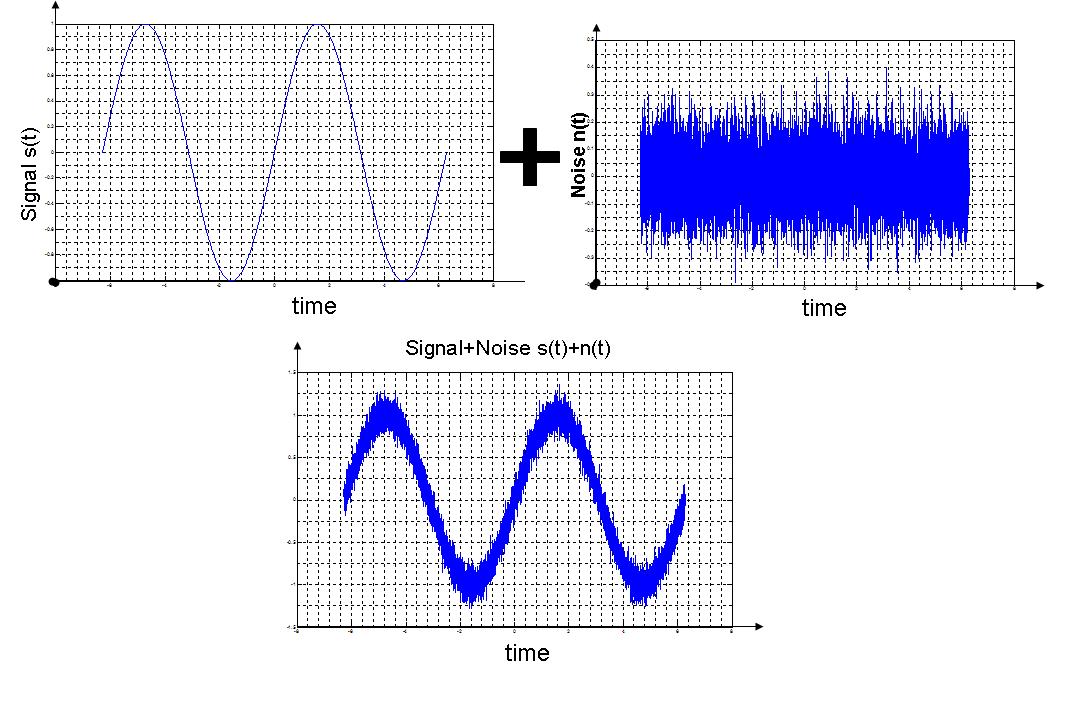
| − | A cosine wave with frequency f can be written as <math>cos(2 \pi f t)</math>. When sampling this cosine with period T, the sampled signal <math>x[n]</math> can be written as <math>x[n]=cos(\frac{2 \pi f n}{T})</math>. | + | A cosine wave with frequency f can be written as <math>cos(2 \pi f t)</math>. When sampling this cosine with period T (frequency <math>f_{s}=1/T</math>, the sampled signal <math>x[n]</math> can be written as <math>x[n]=cos(\frac{2 \pi f n}{T})</math>. |
| + | |||
| + | The nyquist rate for a given signal is given as <math>f_{s} = 2 f_{m}</math>, where <math>f_{m}</math> is the highest frequency in the signal. Since a cosine has only one positive frequency, for a cosine <math>f_{m}=f</math> and the nyquist rate is <math>f_{s}=2 f \ Hz</math>. | ||
| + | |||
| + | For demonstration, consider a cosine with frequency 880 Hz. This represents a pure A note. This signal can be written as: | ||
| + | <math>x(t)=cos(2 \pi 880 t)</math> | ||
| + | |||
| + | In continuous time, the signal looks like this: | ||
| + | |||
| + | [[Image:Example.jpg]] | ||
| + | |||
| + | Using the continuous time signal, it is possible to sample the signal. Due to the Nyquist Theorem, <math>f_{s}>1760\ Hz</math>. To demonstrate sampling above the Nyquist Rate, a <math>f_{s}</math> of 2000 Hz will be used. The sampling points are shown in red on top of the original signal below | ||
| + | |||
| + | [[Image:Example.jpg]] | ||
| + | |||
| + | In order to understand what is happening in the frequency domain, we can compare the CTFT of the cosine to the DTFT of the sampled cosine. | ||
| + | |||
| + | From [[CT_Fourier_Transform_(frequency_in_hertz)|the CTFT table]], the CTFT of a Cosine is | ||
| + | |||
| + | <math>X(f)=\frac{\delta(f-880)+\delta(f+880)}{2}</math> | ||
| + | |||
Revision as of 04:21, 3 October 2014
Discrete-time Fourier transform (DTFT) of a sampled cosine
A slecture by ECE student Sutton Hathorn
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
A cosine wave with frequency f can be written as $ cos(2 \pi f t) $. When sampling this cosine with period T (frequency $ f_{s}=1/T $, the sampled signal $ x[n] $ can be written as $ x[n]=cos(\frac{2 \pi f n}{T}) $.
The nyquist rate for a given signal is given as $ f_{s} = 2 f_{m} $, where $ f_{m} $ is the highest frequency in the signal. Since a cosine has only one positive frequency, for a cosine $ f_{m}=f $ and the nyquist rate is $ f_{s}=2 f \ Hz $.
For demonstration, consider a cosine with frequency 880 Hz. This represents a pure A note. This signal can be written as: $ x(t)=cos(2 \pi 880 t) $
In continuous time, the signal looks like this:
Using the continuous time signal, it is possible to sample the signal. Due to the Nyquist Theorem, $ f_{s}>1760\ Hz $. To demonstrate sampling above the Nyquist Rate, a $ f_{s} $ of 2000 Hz will be used. The sampling points are shown in red on top of the original signal below
In order to understand what is happening in the frequency domain, we can compare the CTFT of the cosine to the DTFT of the sampled cosine.
From the CTFT table, the CTFT of a Cosine is
$ X(f)=\frac{\delta(f-880)+\delta(f+880)}{2} $
(create a question page and put a link below)
Questions and comments
If you have any questions, comments, etc. please post them on this page.