| Line 38: | Line 38: | ||
'''DEFINITION.''' Let <math>F</math> be a function from <math>\mathbb{R}</math> to <math>\mathbb{R}</math>. Then <math>F</math> is continuous at a point <math>c</math> if for every <math>\varepsilon>0</math>, there is a <math>\displaystyle\delta>0</math> such that <math>|F(x)-F(c)|<\varepsilon</math> for any <math>x</math> that satisfies <math>\displaystyle|x-c|<\delta</math>. | '''DEFINITION.''' Let <math>F</math> be a function from <math>\mathbb{R}</math> to <math>\mathbb{R}</math>. Then <math>F</math> is continuous at a point <math>c</math> if for every <math>\varepsilon>0</math>, there is a <math>\displaystyle\delta>0</math> such that <math>|F(x)-F(c)|<\varepsilon</math> for any <math>x</math> that satisfies <math>\displaystyle|x-c|<\delta</math>. | ||
| − | In our language above, <math>\varepsilon</math> is the error bound, and <math>\displaystyle\delta | + | In our language above, <math>\varepsilon</math> is the error bound, and <math>\displaystyle\delta</math> is our measure of "close enough (to <math>c</math>)." |
---- | ---- | ||
| − | == | + | == The Limit of a Function at a Point == |
| − | + | It is a short journey from continuity at a point to the limit of a function at a point. | |
---- | ---- | ||
Revision as of 15:58, 11 May 2014
Contents
[hide]Limit of a Function at a Point
by: Michael Yeh, proud Member of the Math Squad.
keyword: tutorial, limit, function, sequence
INTRODUCTION
Provided here is a brief introduction to the concept of "limit," which features prominently in calculus. We first discuss the limit of a function at a point; to help motivate the definition, we first consider continuity at a point. Unless otherwise mentioned, all functions here will have domain and range $ \mathbb{R} $, the real numbers. Words such as "all," "every," "each," "some," and "there is/are" are quite important here; read carefully!
Continuity at a point
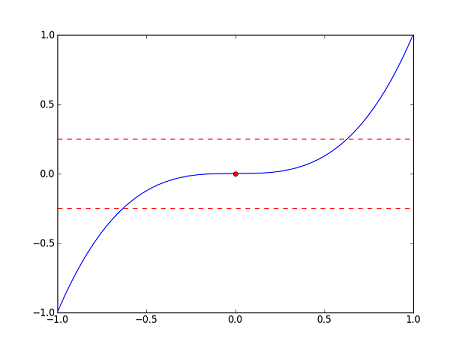
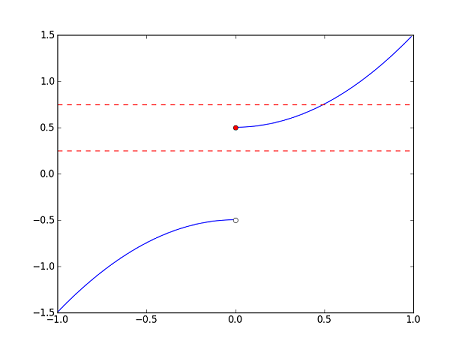
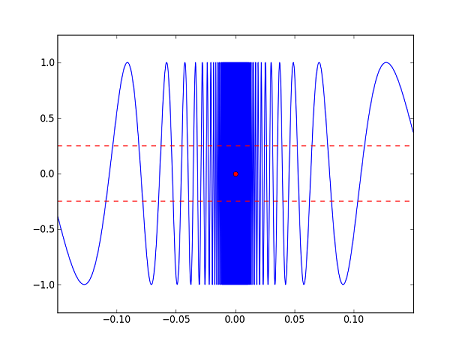
Let's consider the the following three functions along with their graphs (in blue). The red dots in each correspond to $ x=0 $, e.g. for $ f $, the red dot is the point $ (0,f(0))=(0,0) $. Ignore the red dashed lines for now; we will explain them later.
- $ \displaystyle f(x)=x^3 $
- $ g(x)=\begin{cases}-x^2-\frac{1}{2} &\text{if}~x<0\\ x^2+\frac{1}{2} &\text{if}~x\geq 0\end{cases} $
- $ h(x)=\begin{cases} \sin\left(\frac{1}{x}\right) &\text{if}~x\neq 0\\ 0 &\text{if}~x=0\end{cases} $
We can see from the graphs that $ f $ is "continuous" at $ 0 $, and that $ g $ and $ h $ are "discontinuous" at 0. But, what exactly do we mean? Intuitively, $ f $ seems to be continuous at $ 0 $ because $ f(x) $ is close to $ f(0) $ whenever $ x $ is close to $ 0 $. On the other hand, $ g $ appears to be discontinuous at $ 0 $ because there are points $ x $ which are close to $ 0 $ but such that $ g(x) $ is far away from $ g(0) $. The same observation applies to $ h $.
Let's make these observations more precise. First, we will try to estimate $ f(0) $ with error at most $ 0.25 $, say. In the graph of $ f $, we have marked off a band of width $ 0.5 $ about $ f(0) $. So, any point in the band will provide a good approximation here. As a first try, we might think that if $ x $ is close enough to $ 0 $, then $ f(x) $ will be a good estimate of $ f(0) $. Indeed, we see from the graph that for any $ x $ in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $, $ f(x) $ lies in the band (or if we wish to be more pedantic, we would say that $ (x,f(x)) $ lies in the band). So, "close enough to $ 0 $" here means in the interval $ (-\sqrt[3]{0.25},\sqrt[3]{0.25}) $; note that any point which is close enough to $ 0 $ provides a good approximation of $ f(0) $.
There is nothing special about our error bound $ 0.25 $. Choose a positive number $ \varepsilon $, and suppose we would like to estimate $ f(0) $ with error at most $ \varepsilon $. Then, as above, we can find some interval $ \displaystyle(-\delta,\delta) $ about $ 0 $ (if you like to be concrete, any $ \displaystyle\delta $ such that $ 0<\delta<\sqrt[3]{\varepsilon} $ will do) such that $ f(x) $ is a good estimate for $ f(0) $ for any $ x $ in $ \displaystyle(-\delta,\delta) $. In other words, for any $ x $ which is close enough to $ 0 $, $ f(x) $ will be no more than $ \varepsilon $ away from $ f(0) $.
Can we do the same for $ g $? That is, if $ x $ is close enough to $ 0 $, then will $ g(x) $ be a good estimate of $ g(0) $? Well, we see from the graph that $ g(0.25) $ provides a good approximation to $ g(0) $. But if $ 0.25 $ is close enough to $ 0 $, then certainly $ -0.25 $ should be too; however, the graph shows that $ g(-0.25) $ is not a good estimate of $ g(0) $. In fact, for any $ x>0 $, $ g(-x) $ will never be a good approximation for $ g(0) $, even though $ x $ and $ -x $ are the same distance from $ 0 $.
In contrast to $ f $, we see that for any interval $ \displaystyle(-\delta,\delta) $ about $ 0 $, we can always find an $ x $ in $ \displaystyle(-\delta,\delta) $ such that $ g(x) $ is more than $ 0.25 $ away from $ g(0) $.
We see that the same is true for $ h $. Whenever we find an $ x_1 $ such that $ h(x_1) $ lies in the band, we can always find a point $ x_2 $ such that 1) $ x_2 $ is just as close or closer to $ 0 $ and 2) $ h(x_2) $ lies outside the band. So, it is not true that if $ x $ is close enough to $ 0 $, then $ h(x) $ will be a good estimate for $ h(0) $.
Let's summarize what we have found. For $ f $, we saw that for each $ \varepsilon>0 $, there is an interval $ \displaystyle(-\delta,\delta) $ about $ 0 $ (note that $ \displaystyle\delta $ depends on $ \varepsilon $) such that for every $ x $ in $ \displaystyle(-\delta,\delta) $, $ f(x) $ is in $ (f(0)-\varepsilon,f(0)+\varepsilon) $. However, $ g $ does not satisfy this property. More specifically, there is an $ \varepsilon>0 $ such that for each interval $ \displaystyle(-\delta,\delta) $ about $ 0 $, we can find an $ x $ in $ \displaystyle(-\delta,\delta) $ with the property that $ f(x) $ is not in $ (g(0)-\varepsilon,g(0)+\varepsilon) $. The same is true of $ h $.
Now we state the formal definition of continuity at a point. Compare this carefully with the previous paragraph.
DEFINITION. Let $ F $ be a function from $ \mathbb{R} $ to $ \mathbb{R} $. Then $ F $ is continuous at a point $ c $ if for every $ \varepsilon>0 $, there is a $ \displaystyle\delta>0 $ such that $ |F(x)-F(c)|<\varepsilon $ for any $ x $ that satisfies $ \displaystyle|x-c|<\delta $.
In our language above, $ \varepsilon $ is the error bound, and $ \displaystyle\delta $ is our measure of "close enough (to $ c $)."
The Limit of a Function at a Point
It is a short journey from continuity at a point to the limit of a function at a point.
REFERENCES
[1] "Lorem Ipsum" <http://www.lipsum.com/>.
Questions and comments
If you have any questions, comments, etc. please, please please post them below:
- Comment / question 1
- Comment / question 2
The Spring 2014 Math Squad was supported by an anonymous gift to Project Rhea. If you enjoyed reading these tutorials, please help Rhea "help students learn" with a donation to this project. Your contribution is greatly appreciated.