| Line 60: | Line 60: | ||
Using "decimation by two" FFT algorithm, the total number of multiplications is <math>2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503</math> and the total number of additions is <math>2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442</math> | Using "decimation by two" FFT algorithm, the total number of multiplications is <math>2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503</math> and the total number of additions is <math>2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442</math> | ||
| + | ---- | ||
| + | ==Question 5== | ||
| + | |||
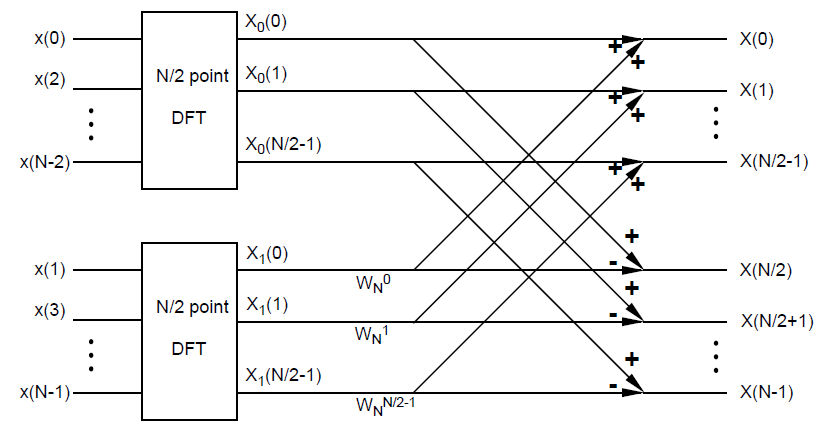
| + | Flow Diagram: | ||
| + | |||
| + | [[Image:HW5Q5fig1.jpg]] | ||
| + | |||
| + | <math>5120=5*1024=5*2^{10}</math> So we can split the 5120-point DFT into 5 1024-point DFTs using decimation-in-time and compute the 1024-point DFT using the subroutine of radix 2 FFT. | ||
| + | |||
| + | Analytical expression: | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | X^{(5120)}(k)&=\sum_{n=0}^{5119} x(n)e^{-\frac{j2\pi kn}{5120}} \\ | ||
| + | &\text{Change variable n=5m+l, m=0,1,...,1023; l=0,1,...,4 } \\ | ||
| + | X^{(5120)}(k)&=\sum_{l=0}^{4}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi k(5m+l)}{5120}} \\ | ||
| + | &=\sum_{l=0}^{4}e^{-\frac{j2\pi kl}{5120}}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi km}{1024}} \\ | ||
| + | &=\sum_{l=0}^{4}W_{5120}^{kl}X_l^{(1024)}(k) \text{ ,k=0,1,...,5119 } | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Direct computation requires N*N=5120*5120=26214400 times of complex multiplications and N*(N-1)=5120*5119=26209280 times of complex additions. | ||
| + | |||
| + | Using FFT we first perform five 1024-point FFTs, which each require <math>\frac{N}{2}log_2 N=512*10=5120</math> complex multiplications and <math>Nlog_2 N=1024*10=10240</math> complex additions. | ||
| + | |||
| + | To calculate each of the 5120 final output of the 5120 DFT, we have to perform 5 complex multiplications and 4 complex additions. | ||
| + | So we need 5120*5= 25600 times of complex multiplications and 5120*4=20480 times of complex additions. | ||
| + | |||
| + | For the FFT based method we have a total of 5120+25600=30720 complex multiplications and 10240+20480=30720 complex addtions. | ||
| + | |||
| + | By compare the two methods, we see that FFT based method is far more efficient than the direct computation. | ||
---- | ---- | ||
Revision as of 17:00, 23 October 2011
Contents
Homework 5, ECE438, Fall 2011, Prof. Boutin
Question 1
Diagram of "decimation by two" FFT computing N-pt DFT. N=8 in this question.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $.
For each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need $ N^2 = 64 $ times of complex multiplications and $ N^2-N = 56 $ times of complex additions.
Using "decimation by two" FFT algorithm, the DFT is computed in two steps. For the first step, two N/2-pt DFT are computed with $ 2\cdot (\frac{N}{2})^2 $ multiplications and $ 2((\frac{N}{2})^2-\frac{N}{2}) $. For the second step, $ \frac{N}{2} $ multiplications and $ N $ additions are needed.
When $ N=8 $, the total numbers of complex operations are
multiplications: $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 36 $
additions: $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 32 $
Question 2
Diagram of "radix-2" FFT computing 8-pt DFT.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)
Question 3
The diagram is identical to the diagram in Question 1 except N=122.
By similar argument presented in Question 1, a direct computation of DFT requires $ N^2 = 14884 $ times of complex multiplications and $ N^2-N = 14762 $ times of complex additions.
Using "decimation by two" FFT algorithm, the total number of multiplications is $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503 $ and the total number of additions is $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442 $
Question 5
Flow Diagram:
$ 5120=5*1024=5*2^{10} $ So we can split the 5120-point DFT into 5 1024-point DFTs using decimation-in-time and compute the 1024-point DFT using the subroutine of radix 2 FFT.
Analytical expression:
$ \begin{align} X^{(5120)}(k)&=\sum_{n=0}^{5119} x(n)e^{-\frac{j2\pi kn}{5120}} \\ &\text{Change variable n=5m+l, m=0,1,...,1023; l=0,1,...,4 } \\ X^{(5120)}(k)&=\sum_{l=0}^{4}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi k(5m+l)}{5120}} \\ &=\sum_{l=0}^{4}e^{-\frac{j2\pi kl}{5120}}\sum_{m=0}^{1023}x(5m+l)e^{-\frac{j2\pi km}{1024}} \\ &=\sum_{l=0}^{4}W_{5120}^{kl}X_l^{(1024)}(k) \text{ ,k=0,1,...,5119 } \end{align} $
Direct computation requires N*N=5120*5120=26214400 times of complex multiplications and N*(N-1)=5120*5119=26209280 times of complex additions.
Using FFT we first perform five 1024-point FFTs, which each require $ \frac{N}{2}log_2 N=512*10=5120 $ complex multiplications and $ Nlog_2 N=1024*10=10240 $ complex additions.
To calculate each of the 5120 final output of the 5120 DFT, we have to perform 5 complex multiplications and 4 complex additions. So we need 5120*5= 25600 times of complex multiplications and 5120*4=20480 times of complex additions.
For the FFT based method we have a total of 5120+25600=30720 complex multiplications and 10240+20480=30720 complex addtions.
By compare the two methods, we see that FFT based method is far more efficient than the direct computation.
Back to Homework 5
Back to ECE 438 Fall 2011