| Line 13: | Line 13: | ||
*<span style="color:red"> Instructor's comment: Actually, strictly speaking, it should be '''greater''' than 5000HZ. -pm</span> | *<span style="color:red"> Instructor's comment: Actually, strictly speaking, it should be '''greater''' than 5000HZ. -pm</span> | ||
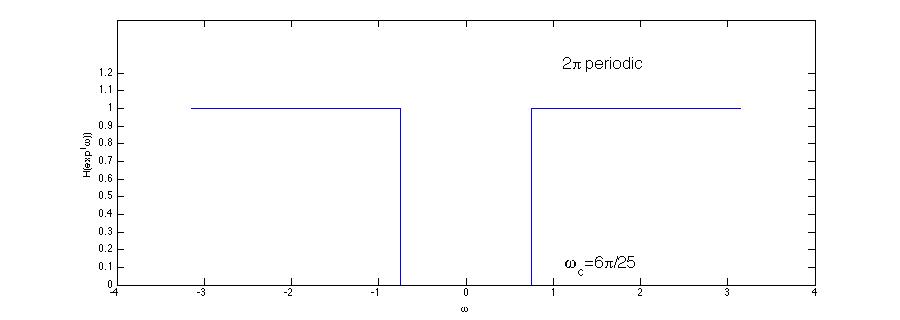
| − | We | + | We need a high pass filter that filters our everything below 60 Hz. |
<math>\begin{align} | <math>\begin{align} | ||
Latest revision as of 12:18, 30 September 2013
Contents
Homework 6, ECE438, Fall 2013, Prof. Boutin
Please leave all mistakes and instructor's comments as is, unless otherwise noted by Prof. Mimi.
Question 1
The sampling rate should be at least twice of the highest frequency of the signal to avoid aliasing. Let's make it just twice of the highest frequency for illustration.
$ \begin{align} f_s=2 \cdot 2500=5000Hz \end{align} $
- Instructor's comment: Actually, strictly speaking, it should be greater than 5000HZ. -pm
We need a high pass filter that filters our everything below 60 Hz.
$ \begin{align} \omega_c=\frac{2\pi \cdot f_c }{f_s}=\frac{2\pi \cdot 60 }{5000} \end{align} $
Question 2
We can think of the long term trend as low frequency component and annual cycle as high frequency component. In order to remove the annual cycle, we need a low pass filter. The sampling rate $ f_s=12 $samples/year. The periodic component has frequency of $ f_c=1 $cycle/year.
\\ So the low pass filter has cutoff frequency of $ \omega_c=\frac{2\pi \cdot 1}{12}=\frac{\pi}{6} $
Question 3
$ \text{a)} \;\; \text{General Relation for the decimation with a factor of } D \,\! $.
$ \text{Let } X(w) = \mathcal{F}(x[n]) $
$ \begin{align} Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[Dn]e^{-jwn} \\ &= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(w-\frac{2\pi}{D}k\right)m} \\ &= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ \end{align} $
Replacing D with 5 would be the answer.
$ \text{b)} \;\; \text{General Relation for the upsampling with a factor of } L \,\! $.
$ \begin{align} Z(w) &= \sum_{n=-\infty}^{\infty} z[n]e^{-jwn} \\ &= \sum_{n=-\infty}^{\infty} \left( \sum_{k=-\infty}^{\infty} x[k] \delta[n-kL] \right) e^{-jwn} \\ &= \sum_{k=-\infty}^{\infty} x[k] \sum_{n=-\infty}^{\infty} \delta[n-kL] e^{-jwn} = \sum_{k=-\infty}^{\infty} x[k] e^{-jwkL} \\ &= \sum_{k=-\infty}^{\infty} x[k] e^{-jLwk} = X(Lw) \\ &\end{align} $
Since $ X(w) $ is periodic with $ 2\pi $, $ Z(w)=X(Lw) $ is periodic with $ 2\pi/L $.
Replaing L with 5 would be the answer.
Question 4
a) For $ k=0,1,...,N-1 $
$ \begin{align} X_N(k) &= \sum_{k=0}^{N-1}x[n]e^{-\frac{j2\pi nk}{N}} \\ &= x[0]e^{-\frac{j2\pi 0\cdot k}{N}} \\ &= 1 \end{align} $
$ X_N(k) $ is periodic with N
- Instructor's comments: How about the other values of k? -pm
b) Using Euler Formula, we have
$ \begin{align} x[n] &= e^{\frac{j\pi n}{3}}(\frac{ e^{\frac{j\pi n}{6}} + e^{-\frac{j\pi n}{6}} }{2}) \\ &= \frac{1}{2}e^{\frac{j\pi n}{2}} + \frac{1}{2}e^{\frac{j\pi n}{6}} \end{align} $
Observing that $ x[n] $ has fundamental period $ N=12 $. Using IDFT, we have
$ \begin{align} x[n] &= \frac{1}{N}\sum_{n=0}^{N-1}e^{\frac{j2\pi nk}{N}} \\ \frac{1}{2}e^{\frac{j\pi n}{2}} + \frac{1}{2}e^{\frac{j\pi n}{6}} &= \frac{1}{12}\sum_{n=0}^{11}e^{\frac{j2\pi nk}{12}} \end{align} $
By comparison, we know for $ k=0,1,...,11 $
$ X_{12}[k] = \left\{ \begin{array}{ll} 6, & k=1,3 \\ 0, & otherwise. \end{array} \right. $
$ X_{12}[k] $ is periodic with 12.
- Instructor's comments: How about k=12, k=13, and all the other values of k? -pm
c)
$ x[n]=(\frac{1}{\sqrt 2} + j\frac{1}{\sqrt 2})^n = (e^{\frac{j\pi}{4}})^n $
Then $ x[n] $ has fundamental period $ N=8 $. Using IDFT, we have
$ \begin{align} x[n] &= \frac{1}{N}\sum_{n=0}^{N-1}e^{\frac{j2\pi nk}{N}} \\ e^{\frac{j\pi n}{4}} &= \frac{1}{8}\sum_{n=0}^{7}e^{\frac{j2\pi nk}{8}} \end{align} $
By comparison, we know for $ k=0,1,...,7 $
$ X_{8}[k] = \left\{ \begin{array}{ll} 8, & k=1 \\ 0, & otherwise. \end{array} \right. $
$ X_{8}[k] $ is periodic with 8.
- Instructor's comments: Don't forget to say that K[k} repeats periodically with period 8. THat way, all values of k are covered. -pm
Question 5
Observing that $ X(k) $ has a fundamental period $ N=4 $
$ \begin{align} x[n] &= \frac{1}{N}\sum_{k=0}^{N-1}(e^{j \pi k }+e^{-j \frac{\pi}{2} k})e^{\frac{j2\pi nk}{N}} \\ &= \frac{1}{4}\sum_{k=0}^{3}(e^{\frac{j2\pi (n+2)k}{4}} + e^{\frac{j2\pi (n-1)k}{4}}) \\ &= \frac{1}{4}\sum_{k=0}^{3}(e^{\frac{j2\pi (n+2)k}{4}-j2\pi k} + e^{\frac{j2\pi (n-1)k}{4}}) \\ &= \frac{1}{4}\sum_{k=0}^{3}(e^{\frac{j2\pi (n-2)k}{4}} + e^{\frac{j2\pi (n-1)k}{4}}) \\ \end{align} $
when $ n\neq 1 \text{ or } 2 $, using geometric series summation formula we have
$ x[n]=\frac{1}{4}( \frac{1-e^{j2\pi (n-2)}}{1-e^{\frac{j2\pi (n-2)}{4}}} + \frac{1-e^{j2\pi (n-1)}}{1-e^{\frac{j2\pi (n-1)}{4}}} ) = 0 $
when $ n=1 \text{ or } 2 $
$ x[n]=\sum_{k=0}^{3}1=4 $
$ x[n] $ will be periodic with 4.
NOTE: In general, $ X(k) $ does not need to have a length equal to the fundamental period. Suppose N is an arbitrary number, we can still derive the IDFT using argument that is similar to the one described above.