Vector Derivatives Cylindrical Coordinates - Rhea

keyword: divergence, curl, gradient

Vector Derivatives in Cylindrical Coordinates

INTRODUCTION

Vector derivatives provide a concise way to express vector equations in a way independent of the particular coordinate system being used, while making underlying physics more apparent. Compare, for example, the Navier-Stokes equations in vector form:

$ \frac{\partial \rho \vec{u}}{\partial t} + \left(\vec{u}\cdot\nabla\right)\rho\vec{u} = -\nabla P + \nabla\cdot(\mu\nabla\vec{u}) $

With the Navier-Stokes equations in terms of partial derivatives in Cartesian coordinates

$ \frac{\partial \rho u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = -\frac{\partial P}{\partial x} + \frac{\partial}{\partial x}\left(\mu \frac{\partial u}{\partial x}\right) + \frac{\partial}{\partial y}\left(\mu \frac{\partial u}{\partial y}\right) + \frac{\partial}{\partial z}\left(\mu \frac{\partial u}{\partial z}\right) $

$ \frac{\partial \rho v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = -\frac{\partial P}{\partial y} + \frac{\partial}{\partial x}\left(\mu \frac{\partial v}{\partial x}\right) + \frac{\partial}{\partial y}\left(\mu \frac{\partial v}{\partial y}\right) + \frac{\partial}{\partial z}\left(\mu \frac{\partial v}{\partial z}\right) $

$ \frac{\partial \rho w}{\partial t} + u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z} = -\frac{\partial P}{\partial z} + \frac{\partial}{\partial x}\left(\mu \frac{\partial w}{\partial x}\right) + \frac{\partial}{\partial y}\left(\mu \frac{\partial w}{\partial y}\right) + \frac{\partial}{\partial z}\left(\mu \frac{\partial w}{\partial z}\right) $

Not only does the first style involve less writing, it is also "portable" among any coordinate system you care to define. The subtle point is that although the equation remains the same, the expressions for the divergence and gradient do depend on the coordinate system. Writing out the three components of the vector Navier-Stokes equations in cylindrical coordinates would introduce different derivatives and coefficients of those derivatives. Those coefficients are not necessarily obvious, and deriving them is usually tedious if not difficult.

In Cartesian coordinates, gradient, divergence, and curl are defined as below, where $ n $ is the number of spatial dimensions involved. If $ x_1, x_2, ..., x_n $ are the coordinate directions and

$ \hat{e}_i , i = 1,2,...,n $

are the unit vectors in those directions, then

$ \nabla\phi = \sum_{i=1}^n \frac{\partial \phi}{\partial x_i} \hat{e}_i $

$ \nabla\cdot\vec{v} = \sum_{i=1}^n \frac{\partial v_i}{\partial x_i} \text{, where } \vec{v} = \sum_{i=1}^n v_i \hat{e}_i $

$ \nabla\times\vec{u} = \left(\frac{\partial u_z}{\partial y} - \frac{\partial u_y}{\partial z }\right)\hat{e}_x + \left(\frac{\partial u_x}{\partial z} - \frac{\partial u_z}{\partial x}\right)\hat{e}_y + \left(\frac{\partial u_y}{\partial x} - \frac{\partial u_x}{\partial y}\right)\hat{e}_z $

Based on this definition, one might expect that in cylindrical coordinates, the gradient operation would be

$ \nabla\phi \neq \frac{\partial \phi}{\partial r}\hat{e}_r + \frac{\partial \phi}{\partial \theta}\hat{e}_{\theta} + \frac{\partial \phi}{\partial z}\hat{e}_z $

By simply taking the partial derivatives of $ \phi $ with respect to each coordinate direction, multiplying each derivative by the corresponding unit vector, and adding the resulting components together. This is actually not correct for coordinate systems other than Cartesian. One could arrive at the correct formula for the gradient by performing many changes of variables, and repeat the process for the other vector derivatives. However that approach has many opportunities for error and does not produce much insight as to why the coefficients are what they are. This tutorial shows a different way to arrive at the same results but more compactly.

Preliminaries

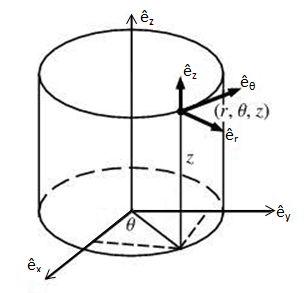
This tutorial will denote vector quantities with an arrow atop a letter, except unit vectors that define coordinate systems which will have a hat. 3-D Cartesian coordinates will be indicated by $ x, y, z $ and cylindrical coordinates with $ r,\theta,z $.

This tutorial will make use of several vector derivative identities. In particular, these:

$ \nabla\cdot(\phi\vec{v}) = \nabla\phi\cdot\vec{v} + \phi \nabla\cdot\vec{u} $

$ \nabla\times(\phi\vec{v}) = \nabla\phi\times\vec{v} + \phi \nabla\times\vec{u} $

On some occasions we will also have to translate between partial derivatives in various coordinate systems. Start with the multivariate chain rule:

$ \frac{\partial \phi}{\partial r} = \frac{\partial \phi}{\partial x}\frac{\partial x}{\partial r} + \frac{\partial \phi}{\partial y}\frac{\partial y}{\partial r} + \frac{\partial \phi}{\partial z}\frac{\partial z}{\partial r} $

$ \frac{\partial \phi}{\partial \theta} = \frac{\partial \phi}{\partial x}\frac{\partial x}{\partial \theta} + \frac{\partial \phi}{\partial y}\frac{\partial y}{\partial \theta} + \frac{\partial \phi}{\partial z}\frac{\partial z}{\partial \theta} $

$ \frac{\partial \phi}{\partial z} = \frac{\partial \phi}{\partial x}\frac{\partial x}{\partial z} + \frac{\partial \phi}{\partial y}\frac{\partial y}{\partial z} + \frac{\partial \phi}{\partial z}\frac{\partial z}{\partial z} $

In matrix form:

$ \begin{bmatrix} \frac{\partial \phi}{\partial r} \\ \frac{\partial \phi}{\partial \theta} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} = \begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} & \frac{\partial z}{\partial r} \\ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta} \\ \frac{\partial x}{\partial z} & \frac{\partial y}{\partial z} & \frac{\partial z}{\partial z} \end{bmatrix} \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z}\end{bmatrix} $

The entries of the square matrix come from the coordinate transformation itself:

$ x = r \cos \theta \rightarrow \frac{\partial x}{\partial r} = \cos \theta \text{ , } \frac{\partial x}{\partial \theta} = -r\sin \theta $

$ y = r \sin \theta \rightarrow \frac{\partial y}{\partial r} = \sin \theta \text{ , } \frac{\partial y}{\partial \theta} = r\cos \theta $

$ z = z \rightarrow \frac{\partial x}{\partial z} = \frac{\partial y}{\partial z} = 0 \text{ , } \frac{\partial z}{\partial z} = 1 $

$ \begin{bmatrix} \frac{\partial \phi}{\partial r} \\ \frac{\partial \phi}{\partial \theta} \\ \frac{\partial \phi}{\partial z}\end{bmatrix} = \begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -r \sin\theta & r \cos\theta & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} $

This gives the partial derivatives with respect to cylindrical coordinate variables in terms of partial derivatives with respect to Cartesian coordinate variables. We can go the other way by inverting this linear system:

$ \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z}\end{bmatrix} = \begin{bmatrix} \cos \theta & -\frac{\sin \theta}{r} & 0 \\ \sin \theta & \frac{\cos\theta}{r} & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} \frac{\partial \phi}{\partial r} \\ \frac{\partial \phi}{\partial \theta} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} $

Note that $ \phi $ can be any scalar field for which all partial derivatives exist, including the coordinate variables themselves.

We are now ready to tackle the gradient in cylindrical coordinates.

Gradient in Cylindrical Coordinates

Obviously, the gradient can be written in terms of the unit vectors of cylindrical and Cartesian coordinate systems as $ a\frac{\partial \phi}{\partial r}\hat{e}_r + b\frac{\partial \phi}{\partial \theta}\hat{e}_{\theta} + c\frac{\partial \phi}{\partial z}\hat{e}_z = \nabla\phi = \frac{\partial \phi}{\partial x}\hat{e}_x + \frac{\partial \phi}{\partial y}\hat{e}_y + \frac{\partial \phi}{\partial z}\hat{e}_z $

Where $ a,b,c $ are coefficients to be determined. We can single out components of the left-hand side by taking dot products with the cylindrical unit vectors. This approach yields three equations:

$ a\frac{\partial \phi}{\partial r} = \frac{\partial \phi}{\partial x}\hat{e}_x\cdot\hat{e}_r + \frac{\partial \phi}{\partial y}\hat{e}_y\cdot\hat{e}_r = \frac{\partial \phi}{\partial x}\cos\theta + \frac{\partial \phi}{\partial y}\sin\theta $

$ b\frac{\partial \phi}{\partial \theta} = \frac{\partial \phi}{\partial x}\hat{e}_x\cdot\hat{e}_{\theta} + \frac{\partial \phi}{\partial y}\hat{e}_y\cdot\hat{e}_{\theta} = -\frac{\partial \phi}{\partial x}\sin\theta + \frac{\partial \phi}{\partial y}\cos\theta $

$ c\frac{\partial \phi}{\partial z} = \frac{\partial \phi}{\partial z} \rightarrow c = 1 $

Solve for $ a,b $ by substituting into the first two of these equations the first two rows of the change-of-variable matrix:

$ \frac{\partial \phi}{\partial x}\cos\theta + \frac{\partial \phi}{\partial y}\sin\theta = a\left(\frac{\partial \phi}{\partial x} \cos\theta + \frac{\partial \phi}{\partial y} \sin\theta \right) \rightarrow a = 1 $

$ -\frac{\partial \phi}{\partial x}\sin\theta + \frac{\partial \phi}{\partial y}\cos\theta = b\left(-\frac{\partial \phi}{\partial x} r\sin\theta + \frac{\partial \phi}{\partial y} r\cos\theta\right) \rightarrow b = \frac{1}{r} $

So the gradient expression we sought turns out to be

$ \nabla\phi = \frac{\partial \phi}{\partial r}\hat{e}_r + \frac{1}{r}\frac{\partial \phi}{\partial \theta}\hat{e}_{\theta} + \frac{\partial \phi}{\partial z}\hat{e}_z $

Divergence in Cylindrical Coordinates

We want an expression for

$ \nabla\cdot\vec{u} = \nabla\cdot\left(u_r\hat{e}_r + u_{\theta}\hat{e}_{\theta} + u_z\hat{e}_z\right) $

That involves only derivatives in cylindrical coordinates. Using the vector identity mentioned in the preliminaries, this equation can be expanded as:

$ \nabla\cdot\vec{u} = \left(\nabla u_r\right)\cdot\hat{e}_r + u_r\left(\nabla\cdot\hat{e}_r\right) + \left(\nabla u_{\theta}\right)\cdot\hat{e}_{\theta} + u_{\theta}\left(\nabla\cdot\hat{e}_{\theta}\right) + \left(\nabla u_z\right)\cdot\hat{e}_z + u_z\left(\nabla\cdot\hat{e}_z\right) $

The terms involving gradients of the components of the vector field simplify to the partial derivatives of components with respect to their corresponding directions, multiplied by the coefficients found in the previous section:

$ \nabla\cdot\vec{u} = \frac{\partial u_r}{\partial r} + \frac{1}{r}\frac{\partial u_{\theta}}{\partial \theta} + \frac{\partial u_z}{\partial z} + u_r\left(\nabla\cdot\hat{e}_r\right) + u_{\theta}\left(\nabla\cdot\hat{e}_{\theta}\right) + u_z\left(\nabla\cdot\hat{e}_z\right) $

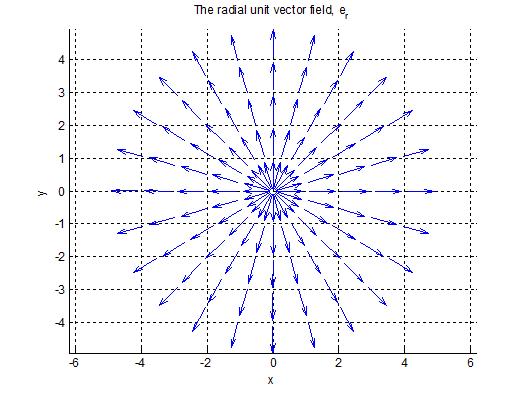
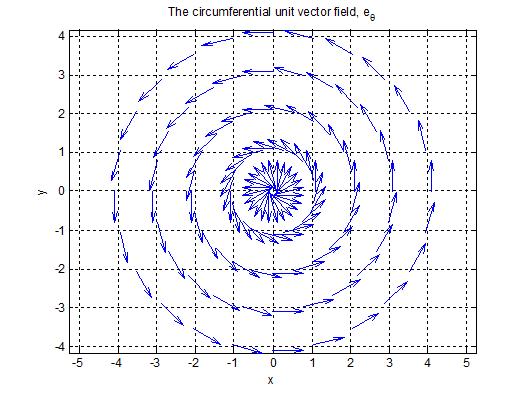
So a divergence "correction" must be applied, which arises from the divergence of the unit vector fields. Technically the unit "vectors" referred to in this tutorial are actually vector fields, since the unit vectors of a coordinate system are defined at all points in space (other than zero, at least).

So we're interested now in the divergences these fields in order to complete the previous equation. But, since the divergence operator is the same for all coordinate systems, we can use its implementation in Cartesian coordinates just as well as the one in cylindrical coordinates. Obviously we so far only know divergence in Cartesian form, so that's what we'll use.

One is very easy:

$ \nabla\cdot\hat{e}_z = \nabla\cdot(0\hat{e}_x + 0\hat{e}_y + 1\hat{e}_z)=\frac{\partial}{\partial z} 1 = 0 $

And the other two require use of the chain rule:

$ \nabla\cdot\hat{e}_r = \nabla\cdot(\cos \theta \hat{e}_x + \sin \theta \hat{e}_y) = \frac{\partial \cos\theta}{\partial x} + \frac{\partial \sin \theta}{\partial y} = -\frac{\partial \theta}{\partial x}\sin\theta + \frac{\partial \theta}{\partial y}\cos\theta $

$ \nabla\cdot\hat{e}_{\theta} = \nabla\cdot(-\sin \theta \hat{e}_x + \cos \theta \hat{e}_y) = -\frac{\partial \sin\theta}{\partial x} + \frac{\partial \cos\theta}{\partial y} = -\frac{\partial \theta}{\partial x}\cos\theta - \frac{\partial \theta}{\partial y}\sin\theta $

In the Preliminaries section, we derived a matrix equation relating the derivatives of a scalar function $ \phi $ in Cartesian coordinates to its derivatives in cylindrical coordinates. Since $ \phi $ was allowed to be any scalar function, we can set $ \phi = \theta $ to obtain

$ \begin{bmatrix} \frac{\partial \theta}{\partial x} \\ \frac{\partial \theta}{\partial y} \\ \frac{\partial \theta}{\partial z}\end{bmatrix} = \begin{bmatrix} \cos \theta & -\frac{\sin \theta}{r} & 0 \\ \sin \theta & \frac{\cos\theta}{r} & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} \frac{\partial \theta}{\partial r} \\ \frac{\partial \theta}{\partial \theta} \\ \frac{\partial \theta}{\partial z} \end{bmatrix} \leftrightarrow $ $ \begin{bmatrix} \frac{\partial \theta}{\partial x} \\ \frac{\partial \theta}{\partial y} \\ \frac{\partial \theta}{\partial z}\end{bmatrix} = \begin{bmatrix} \cos \theta & -\frac{\sin \theta}{r} & 0 \\ \sin \theta & \frac{\cos\theta}{r} & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 0\end{bmatrix}=\begin{bmatrix} -\frac{\sin\theta}{r} \\ \frac{\cos\theta}{r} \\ 0\end{bmatrix} $

Now substitute these expressions for the derivatives of $ \theta $ into the expressions for divergences of the unit vector fields:

$ \nabla\cdot\hat{e}_r = -\left(-\frac{\sin\theta}{r}\right)\sin\theta + \left(\frac{\cos\theta}{r}\right)\cos\theta = \frac{\sin^2\theta}{r} + \frac{\cos^2\theta}{r} = \frac{1}{r} $

$ \nabla\cdot\hat{e}_{\theta} = -\left(-\frac{\sin\theta}{r}\right)\cos\theta - \left(\frac{\cos\theta}{r}\right)\sin\theta = 0 $

So the expression for the divergence is:

$ \nabla\cdot\vec{u} = \frac{\partial u_r}{\partial r} + \frac{1}{r}\frac{\partial u_{\theta}}{\partial \theta} + \frac{\partial u_z}{\partial z} + \frac{1}{r}u_r $

The reason that the divergence expression is not as simple as it is in Cartesian coordinates is that one of the unit vector fields is not divergenceless (or solenoidal). Put another way, if you imagine the radial unit vectors as the velocity of some fluid, then an infinitesimal region at each point has a greater volume of fluid leaving it than entering it.

Curl in Cylindrical Coordinates

We could derive the formula for curl in a similar fashion.

$ \begin{align}\nabla\times\vec{u} &= \nabla\times\left(u_r\hat{e}_r + u_{\theta}\hat{e}_{\theta} + u_z\hat{e}_z\right) \\ &= \left(\nabla u_r\right)\times\hat{e}_r + u_r\left(\nabla\times \hat{e}_r\right) + \left(\nabla u_{\theta}\right)\times\hat{e}_{\theta} + u_{\theta}\left(\nabla\times\hat{e}_{\theta}\right) + \left(\nabla u_z\right)\times\hat{e}_z + u_z\left(\nabla\times\hat{e}_z\right)\end{align} $

However as you can see, the presence of cross products makes some tedious and error-prone computations unavoidable. Suffice to say that, although far from obvious, the curl reduces to

$ \nabla\times\vec{u} = \frac{1}{r}\left|\begin{matrix} \hat{e}_r &r\hat{e}_{\theta} &\hat{e}_z \\ \frac{\partial}{\partial r} &\frac{\partial}{\partial \theta} &\frac{\partial}{\partial z} \\ u_r &r u_{\theta} &u_z \end{matrix}\right| $

When treated as a "determinant". In the course of the calculations, it turns out that

$ \nabla\times\hat{e}_r = 0 = \nabla\times\hat{e}_z $

$ \nabla\times\hat{e}_{\theta} = \frac{1}{r}\hat{e}_z $

The General Case

The coefficient of 1/r in the cylindrical versions of the vector derivatives essentially reflects how the Cartesian space warps as it is transformed into the cylindrical space, which is also measured by the divergence of the radial unit vector field. In general, for any coordinate system there are "scale factors" $ h_1, h_2, h_3 $ such that

$ \nabla\phi = \frac{1}{h_1}\frac{\partial \phi}{\partial x_1}\hat{e}_1 + \frac{1}{h_2}\frac{\partial \phi}{\partial x_2}\hat{e}_2 + \frac{1}{h_3}\frac{\partial \phi}{\partial x_3}\hat{e}_3 $

$ \nabla\cdot\vec{u} = \frac{1}{h_1h_2h_3}\left(\frac{\partial}{\partial x_1} \left(h_2h_3u_1\right) + \frac{\partial}{\partial x_2}\left(h_1h_3u_2\right) + \frac{\partial}{\partial x_3}\left(h_1h_2u_3\right)\right) $

$ \nabla\times\vec{u} = \frac{1}{h_1h_2h_3}\left|\begin{matrix} h_1 \hat{e}_1 &h_2\hat{e}_2 &h_3\hat{e}_3 \\ \frac{\partial}{\partial x_1} &\frac{\partial}{\partial x_2} &\frac{\partial}{\partial x_3} \\ h_1 u_1 &h_2 u_2 &h_3 u_3 \end{matrix}\right| $

Where $ u_1,u_2,u_3 $ are the components of $ \vec{u} $ in the $ x_1,x_2,x_3 $ directions respectively. You can check that for cylindrical coordinates $ h_1 = 1, h_2 = r, h_3 = 1 $. These scale factors can be found from the change-of-variables matrices for any coordinate system, using the same steps as in the gradient section of this tutorial.

References

Gradient from Wolfram MathWorld

Divergence from Wolfram MathWorld

Curl from Wolfram MathWorld

Questions and comments

If you have any questions, comments, etc. please, please please post them below:

• Comment / question 1
• Comment / question 2

Back to Math Squad page