Text slecture - Rhea

1. Introduction
2. Definition of Downsampling
   
3. Derivation of DTFT of downsampled signal
   
4. Example
5. Decimator
6. Conclusion
   

Introduction

This slecture provides definition of downsampling, derives DTFT of  downsampled signal and demonstrates it in a frequency domain. Also, it explains process of decimation and why it needs a low-pass filter.

Definition of Downsampling

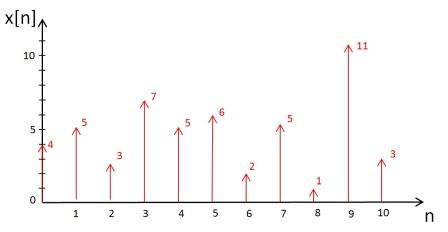
Downsampling is an operation which involves throwing away samples from discrete-time signal. Let  x[n] be a digital-time signal shown below:

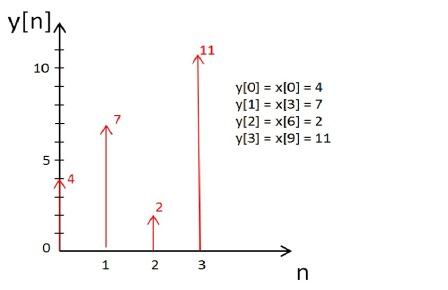
 then y[n] will be produced by downsampling x [n]  by factor D = 3. So, y [n] = x[Dn].

As seen in above graph, y [n] is obtained by throwing away some samples from x [n]. So, y [n] is a downsampled signal from

x [n].

Derivation of DTFT of downsampled signal

Let x (t) be a continuous time signal. Then x₁ [n] = x (T₁n) and  x₂ [n] = x (T₂n). And ratio of sampling periods would be

D = T₂/T₁,   which is an integer greater than 1. From these equations we obtain realtionship between x₁ [n] and x₂ [n].

$ \begin{align} x_2 [n] = x(T_2 n) = x(DT_1 n) = x_1 [nD] \end{align} $

Below we derive Discrete-Time Fourier Transform of x₂ [n] in terms of DTFT of x₁ [n].

$ \begin{align} &\mathcal{X}_2(\omega)= \mathcal{F}(x_2 [n]) = \mathcal{F}(x_1 [Dn])\\ &= \sum_{n = -\infty}^\infty x_1[Dn] e^{-j \omega n} = \sum_{m = -\infty}^\infty x_1[m] e^{-j \omega {\frac{m}{D}}}\\ &= \sum_{n = -\infty}^\infty s_D[m]* x_1 [m] e^{-j \omega {\frac{m}{D}}}\\ \end{align} $

where

$ s_D [m]=\left\{ \begin{array}{ll} 1,& \text{ if } n \text{ is a multiple of } D,\\ 0, & \text{ else}. \end{array}\right. = {\frac{1}{D}} \sum_{k = -\infty}^{D-1} e^{jk {\frac{2 \pi}{D} m}} $

$ \begin{align} &\mathcal{X}_2(\omega)= \sum_{m = -\infty}^\infty {\frac{1}{D}} \sum_{k = -\infty}^{D-1} e^{jk {\frac{2 \pi}{D} m}} x_1[m] e^{-j \omega {\frac{m}{D}}}\\ &= {\frac{1}{D}} \sum_{k = -\infty}^{D-1} \sum_{m = -\infty}^\infty x_1[m] e^{-jm ({\frac{\omega - 2 \pi k}{D}})} = \\ &= {\frac{1}{D}} \sum_{k = -\infty}^{D-1} \mathcal{X}_1 ({\frac{\omega - 2 \pi k}{D}}) \\ \end{align} $

Example

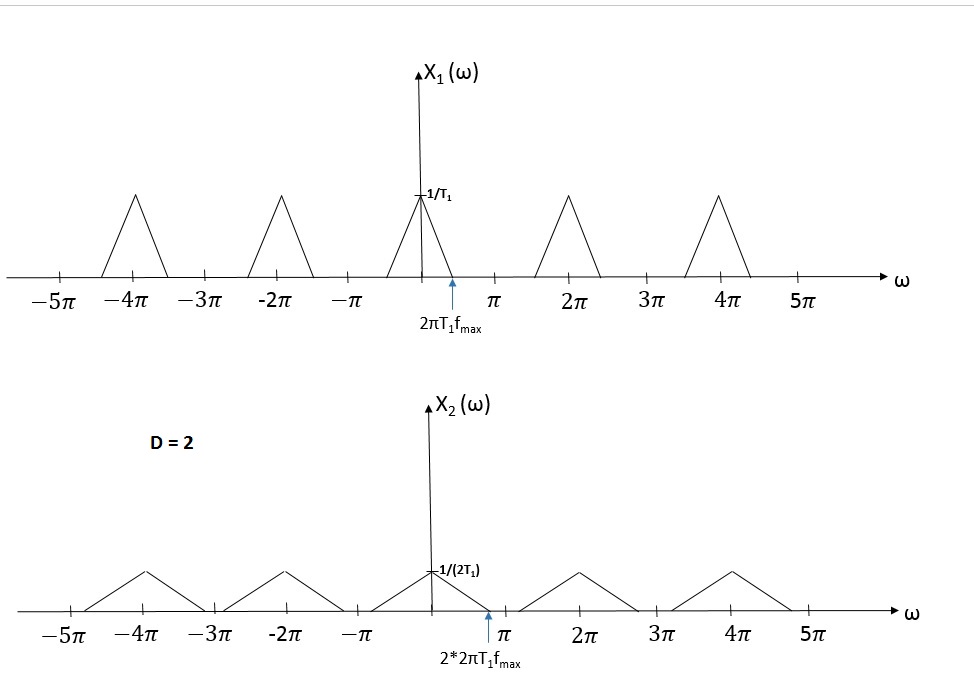
Let's take a look  at  an original signal X₁ (w) and  X₂ (w) which is obtained after downsampling X₁(w) by factor D = 2 in a frequency domain.

From two graphs it is seen that signal is stretched by D  in frequency domain and  decreased by D in a magnitude after downsampling. Both signals have the frequency of $ \begin{align} 2\pi \end{align} $ .

Decimator

As seen in second graph, if $ \begin{align} D2\pi T_1f_{max} \end{align} $ is greater than $ \begin{align} \pi \end{align} $ aliasing occurs. Downsampler is a part of a decimator which also has a low-pass filter to  prevent aliasing.  LPF eliminates signal components which has  frequencies higher than cutoff frequency, which can be found from graphs shown above.

                             $ \begin{align} & D\omega_c = D 2 \pi T_1 f_{max} < \pi\\ & {\frac{T_2}{T_1}} 2\pi T_1 f_{max} < \pi \\ & 2\pi T_2f_{max} < \pi \\ &f_{max} < {\frac{1}{2T_2}} \end{align} $

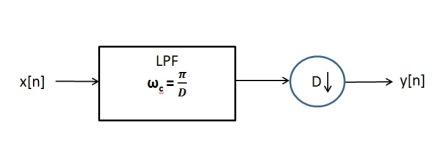
Thereby, signal needs to be filtered before downsampling if f_max > 1/(2T₂) . Complete block diagram of a decimator is shown below:

Conclusion