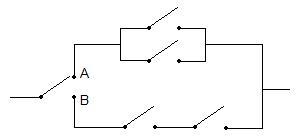
The Problem: What is the probability each circuit will be connected? The probability each switch will be connected is $ p\! $ and $ P(A)=\frac{2}{3} $ and $ P(B)=\frac{1}{3} $.
The probablity of the top path (path $ A\! $) being connected is $ 1-(1-p)^2\! $, which is found by finding the probability the path won't be connected and subtracting it from 1. The probability of the bottom path (path $ B\! $) is obviously $ p^2\! $. Thus
$ P(OC)=\frac{2}{3}[1-(1-p)^2]+\frac{1}{3}p^2 $
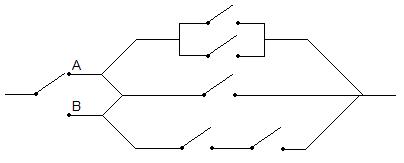
For this design note it is simply the previous problem with another option added in the middle. Thus we can say
$ P(OC)=P(OC|MC)P(MC)+P(OC|MNC)P(MNC)\! $ where
$ OC = \! $ Overall Connected
$ MC = \! $ Middle Connected
$ MNC = \! $ Middle Not Connected
and
$ P(OC|MC)\! $ is $ 1\! $ (if the middle is connected then the entire circuit is!)
$ P(MC)\! $ is just $ p\! $ (probability of the middle switch being connected)
$ P(OC|MNC)\! $ is simply the answer from the first part
$ P(MNC)\! $ is one minus the probability the middle is connected, so $ 1-p\! $
Thus:
$ P(OC)=1p + (1-p)[\frac{2}{3}[1-(1-p)^2]+\frac{1}{3}p^2]\! $