Slecture rep comb ECE438 Xiaozhe - Rhea

1 Outline

     1.1 Definition of Rep operator
      
         1.1.1 Introduction to Rep operator

         1.1.2 Definition of Rep operator

         1.1.3 Two representations of Rep operator

         1.1.4 Relationship between two representations

     1.2 Definition of Comb operator

         1.2.1 Introduction to Comb operator
     
         1.2.2 Definition of Comb operator

         1.2.3 Two representations of Comb operator

         1.2.4 Relationship between two representations

1.1.1 Introduction to Rep operator

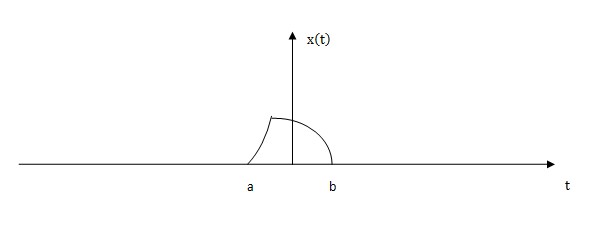
In order to understand Rep operator clearly, a graphical method is introduced as follows:

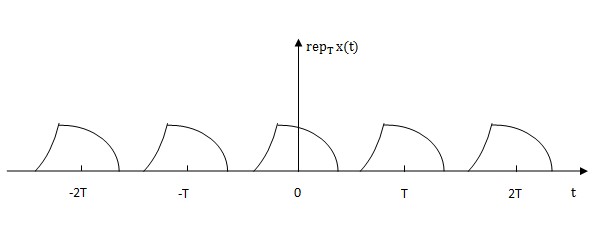
In the figure above, there is a little pulse with compact supports over a definite interval. When repeating it at capital T, We can get the following figure.

This process which is denoted by Rep operator have the same meaning as taking original function x(t) and shifting it by kT in which $ k \in N \quad and \quad -\infty <k< \infty $.

1.1.2 Definition of Rep operator

Rep operator denotes a kind of process which periodically replicates a function with some specific period T. Where the function has a finite domain of argument and the minimum repeating period T has to > a+b(a is the left boundary of the curve and b is the right boundary of the curve ).

1.1.3 Two representations of Rep operator

$ 1.rep_{T}(x[t])=\sum_{k=-\infty}^{\infty}x(t-kT) $

$ 2.rep_{T}(x[t])=x(t) \ast P_{T}(T) $

1.1.4 Relationship between two representations

$ rep_{T}(x[t])=x(t) \ast P_{T}(T) \qquad \qquad \qquad Where \quad P_{T}(T)=\sum_{k=-\infty}^{\infty}\delta(t-kT) $

            $ =x(t) \ast \sum_{k=-\infty}^{\infty}\delta(t-kT) $
            $ =\int_{-\infty}^{\infty}x(\tau)\sum_{k=-\infty}^{\infty}\delta(t-kT-\tau)d\tau $
            $ =\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}x(\tau)\delta(t-kT-\tau)d\tau $

$ Since \quad x(t)=\int_{-\infty}^{\infty}\delta(t-\tau)d\tau $

$ So \quad rep_{T}(x[t])=\sum_{k=-\infty}^{\infty}x(t-kT) $

We can transform the representation with convolution formula to another and vice versa.

1.2.1 Introduction to Comb operator

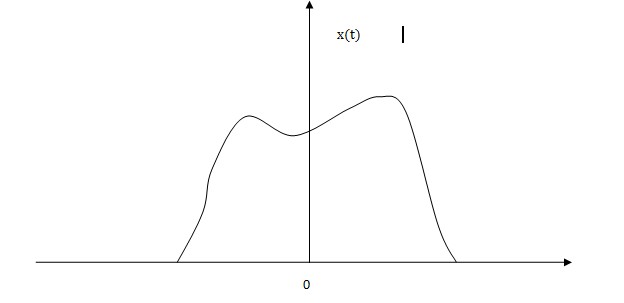
We just use the same method as the one we did previously.The graphical method is introduced as follows:

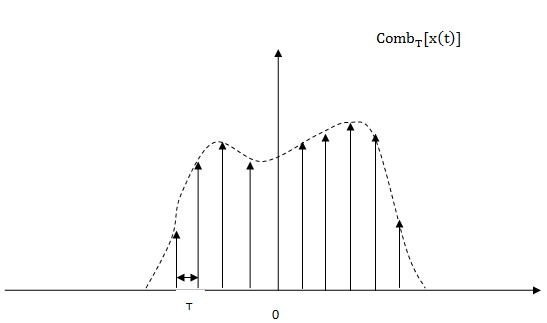
We can draw a conclusion from two figures above that x(t) is modulated by a impulse train with a period T. Just like putting a comb onto the signal and making it been 'sampled'. But this process is a little different from sampling. The continuous signal will become discrete after sampling while it will still be continuous after comb process.

1.2.2 Definition of Comb operator

Comb operator denote a process that 'sampling' a signal by using a impulse train with a specified period T. But the signal after this process will still be continuous.

1.2.3 Two representations of Comb operator

Comb operator is used in time domain:

$ 1.comb_{T}[x(t)]=x(t).\sum_{k=-\infty}^{\infty}\delta(t-kT)=x(t).P_{T}(t) $

Comb operator is used in frequency domain:

$ 2.\frac{1}{T}comb_\frac{1}{T}[X(f)]=\mathcal{F}(rep_{T}[x(t)])=\mathcal{F}(x(t)*P_T(t))=X(f).P_T(f) $

1.2.4 Relationship between two representations

Both of two represents describe the nature of comb operator that is 'sampling' a signal by using a impulse train. But the difference between two represents is that the former one is defined over time domain while the latter is defined over frequency domain.

References

[1].Charles A. Bouman, CSFT and Rep and Comb Relations by video. December 22,2012

[2].Mireille Boutin, "ECE438 Digital Signal Processing with Applications," Purdue University August 26,2009

[3].John G. Proakis, Dimitris G. Manolakis, "Digital Signal Processing with Principles, Algorithms, and Applications" 4th Edition,2006

[4].Alan V. Oppenheim, Alan S. Willsky, S. Hamid Nawab, "Signals and Systems" 2nd Edition,1996

Questions and comments

If you have any questions, comments, etc. please post them on this page.